Module–5

Vector calculus

Question Bank

Question-1:If 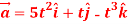and then find-

1.

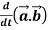
2.

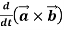
Sol. 1. We know that-

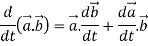
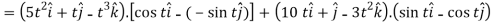
2.

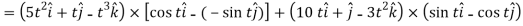
Question-2: A particle is moving along the curve x = 4 cos t, y = 4 sin t, z = 6t. Then find the velocity and acceleration at time t = 0 and t = π/2.

And find the magnitudes of the velocity and acceleration at time t.

Sol. Suppose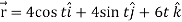

Now,

At t = 0	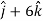4
At t = π/2	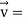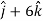-4
At t = 0	|v|=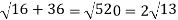
At t = π/2	|v|=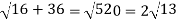

Again acceleration-

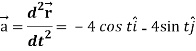
Now-

At t = 0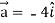
At t = π/2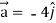
At t = 0	|a|=
At t = π/2	|a|=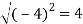

Question-3: If , then show that

1.

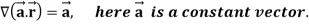
2.

Sol.

Suppose 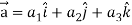  and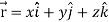

Now taking L.H.S,

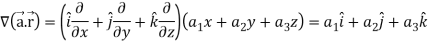
Which is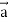

                                                                                               Hence proved.

2.

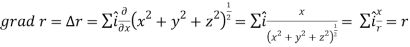
So that

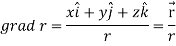
Question-4: If 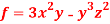then find grad f at the point (1,-2,-1).

Sol.

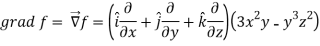
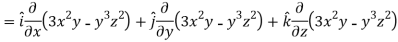
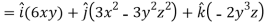
Now grad f at (1 , -2, -1) will be-       

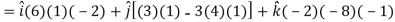
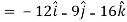
Question-5: If then prove that grad u , grad v and grad w are coplanar.

Sol.

Here-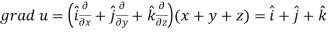                     

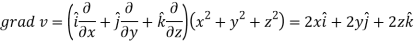
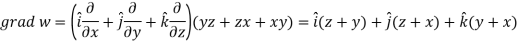
Now-

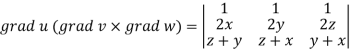
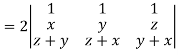
Apply

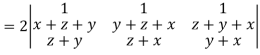
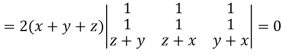
Which becomes zero.

So that we can say that grad u, grad v and grad w are coplanar vectors.

Question-6: Find the directional derivative of 1/r in the direction where

Sol. Here

Now,

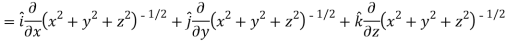
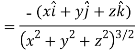
And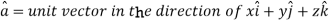

We know that-

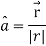
So that-

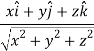
Now,

            Directional derivative =

Question-7: Show that-

1.

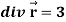
2.

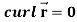
Sol. We know that-

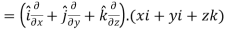
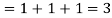
2. We know that-

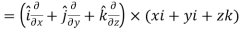
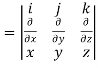
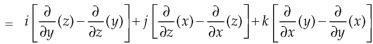
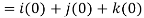= 0

Question-8: If then find the divergence and curl of .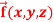

Sol.  we know that-

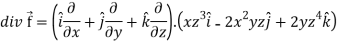
Now-

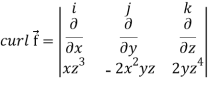
Question-9: Evaluat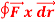e where = (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).

Solution :  F x dr =

Put x=t, y=t2, z= t3

Dx=dt ,dy=2tdt,                dz=3t2dt.

F x dr =

             =(3t4-6t8) dt i  – ( 6t5+3t8 -3t7) dt j +( 4t4+2t7-t2)dt k

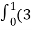=t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k

=

=+

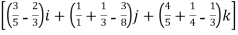
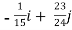Question-10: Evaluate , where S is the surface of the sphere in the first octant.

Sol. Here-

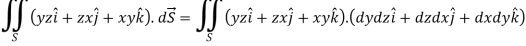
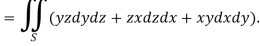
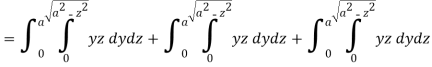
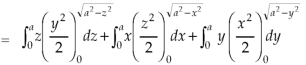
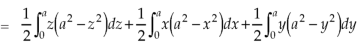
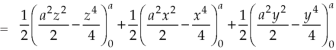
Which becomes-

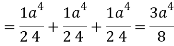
Question-11: Evaluate , where and V is the closed reason bounded by the planes 4x + 2y + z = 8, x = 0, y = 0, z = 0.

Sol.

Here-   4x + 2y + z = 8

Put y = 0 and z = 0 in this, we get

4x = 8 or x = 2

Limit of x varies from 0 to 2 and y varies from 0 to 4 – 2x

And z varies from 0 to 8 – 4x – 2y

So that-

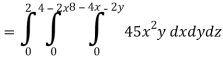
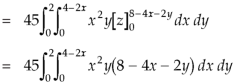
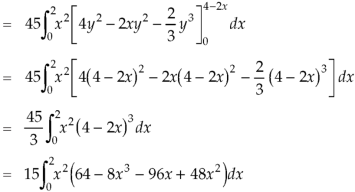
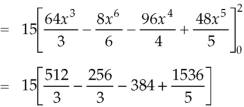
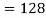
So that-

Question-12: Evaluate by using Green’s theorem, where C is a triangle formed by

Sol. First we will draw the figure-

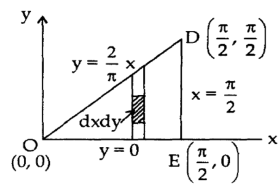
Here the vertices of triangle OED are (0,0), (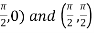

Now by using Green’s theorem-

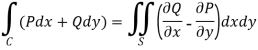
Here P = y – sinx, and Q  = cosx

So that-

  and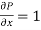

Now-

                              =

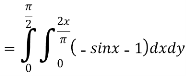
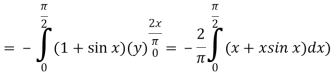
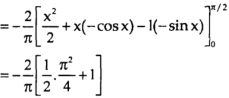
Which is the required answer.

Question-13: If 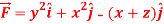and C is the boundary of the triangle with vertices at (0, 0, 0), (1, 0, 0) and (1, 1, 0), then evaluate 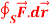by using Stoke’s theorem.

Sol. Here we see that z-coordinates of each vertex of the triangle is zero, so that the triangle lies in the xy-plane and

Now,

              Curl

                       Curl

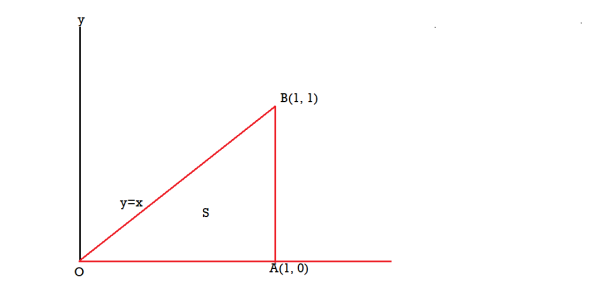
The equation of the line OB is y = x

Now by stoke’s theorem,

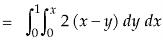
Question-14: Verify Stoke’s theorem for the given function-

Where C is the unit circle in the xy-plane.

Sol. Suppose-

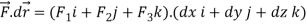
Here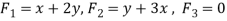

We know that unit circle in xy-plane-

Or

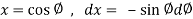
So that,

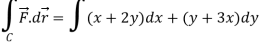
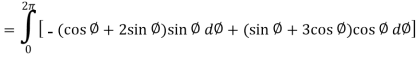
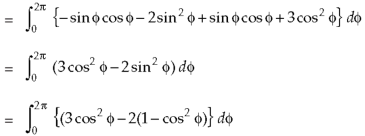
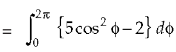
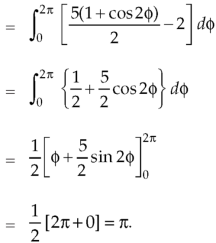
Now

Curl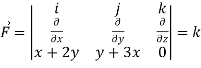

Now,

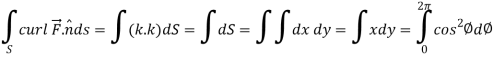
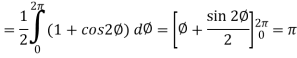
Hence, the Stoke’s theorem is verified.