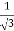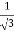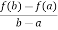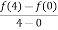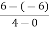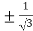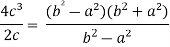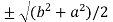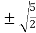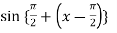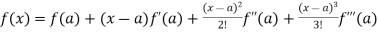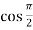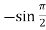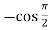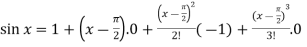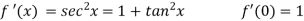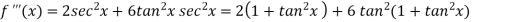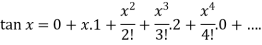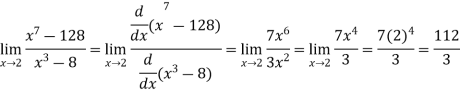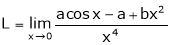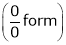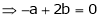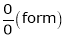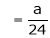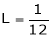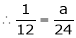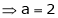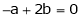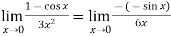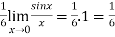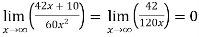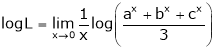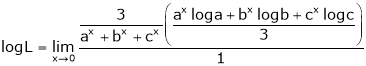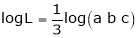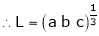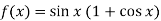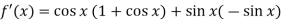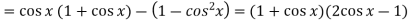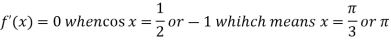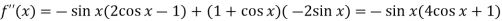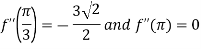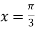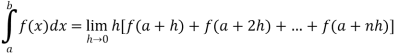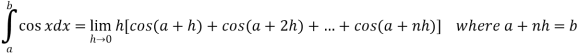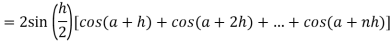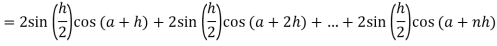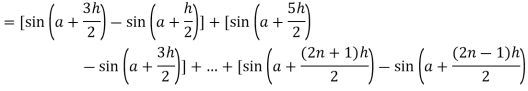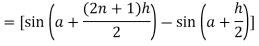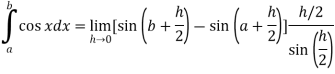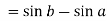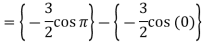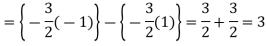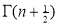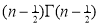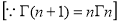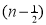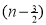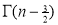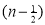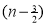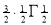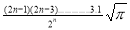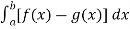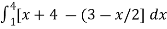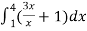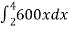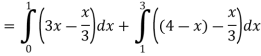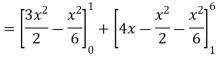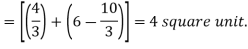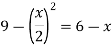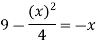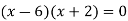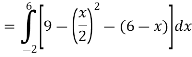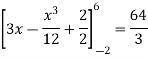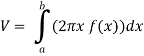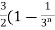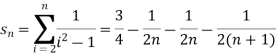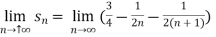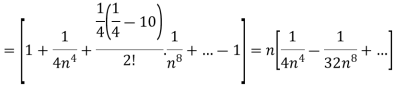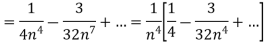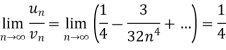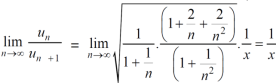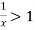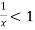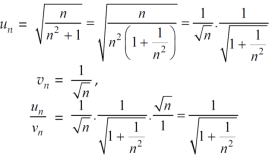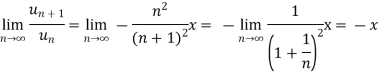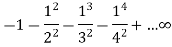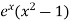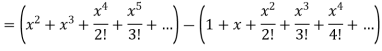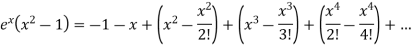Also, f(1) = f(3) = 0 Now we find f’(x) = 0 3x² - 12x +11 = 0 We get, x = 2+ |
Also, f(1) = 1 -4 +8 = 5 and f(3) = 9 – 12 + 8 = 5 Hence f(1) = f(3) Now the first derivative of the function, f’(x) = 0 2x – 4 = 0 , gives X = 2 We can see that 1<2<3, hence there exists 2 between 1 and 3. And f’(2) = 0. |
continuous in [0,4] and differentiable in (0,4). f(x) = (x-1)(x-2)(x-3) f(x) = x-6x²+11x-6 now at x = 0, we get f(0) = -6 and at x = 4, we get. f(4) = 6 diff. the function w.r.t.x , we get f’(x) = 3x²-6x+11 suppose x = c, we get f’(c) = 3c²-6c+11 by Lagrange’s mean value theorem, f’(c) = now we get, 3c²-6c+11 = 3 3c²-6c+8 = 0 On solving the quadratic equation, we get C = 2 |
f’(x) = 4x³ and g’(x) = 2x put these values in Cauchy’s formula, we get
2c² = c² = c = now put the values of a = 1 and b = 2 ,we get c = Hence the Cauchy’s theorem is verified. |
 A4)
A4)Let f(x) = sin x Then, = By using Taylor’s theorem-
Here f(x) = sin x and a = π/2 f’(x) = cosx , f’’(x) = - sin x , f’’’(x) = - cos x and so on. Putting x = π/2 , we get f(x) = sin x = f’(x) = cos x = f’’(x) = -sin x = f’’’(x) = -cos x = from equation (1) put a =
= |
Put these values in Maclaurin’s series we get-
|
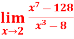 A6)Here we notice that it is an indeterminate form of
A6)Here we notice that it is an indeterminate form of  .So that , we can apply L’Hospital rule-
.So that , we can apply L’Hospital rule-
|
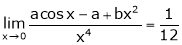 A7)Let
A7)Let
But
|
 A8)We can see that this is an indeterminate form of type 0/0.Apply L’Hospital’s rule, we get
A8)We can see that this is an indeterminate form of type 0/0.Apply L’Hospital’s rule, we get
But this is again an indeterminate form, so that we will again apply L’Hospital’s rule- We get
|
 A9:
A9:Apply L’Hospital rule as we can see that this is the form of
Note- In some cases like above example, we can not apply L’Hospital’s rule. |
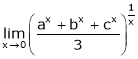 A10)Let
A10)Let
i.e.
|
 .A11)Let
.A11)Let
Then first derivative-
So that-
Now-
So that- So that-
Therefore f(x) has a maximum at |
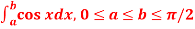 .A12)Here we notice that f:x→cos x is a decreasing function on [a , b],Therefore by the definition of the definite integrals-
.A12)Here we notice that f:x→cos x is a decreasing function on [a , b],Therefore by the definition of the definite integrals-
Then
Now,
Here Thus
|
 A13)
A13)
|

 A14)
A14)
= = = =
|
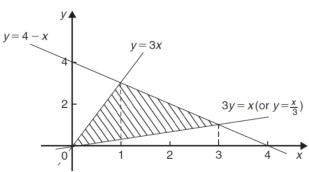
A = = = = = (16 – 7/4) = 57/4 So that the area of the region is 57/4 unit square. |
F = kx So that, 1200 = 2k K = 600 N/cm In that case, F = 600x We know that, W = W = W = 3600 N.cm |
y = 4 – x, y = 3x and 3y = x
Area of shaded region-
|
 and g(x) = 6 – xA18)We get the following figure by using these two equations
and g(x) = 6 – xA18)We get the following figure by using these two equations
To find the intersection points of two functions f(x) and g(x)- f(x) = g(x)
On factorizing, we get-
x = 6, -2 Now
Then, area under the curve- A =
Therefore the area under the curve is 64/3 square unit. |
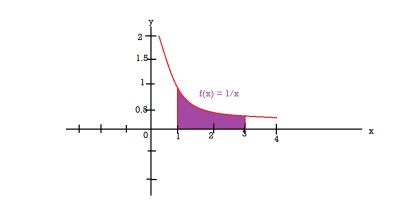
The graph of the function f(x) = 1/x will look like-
The volume of the solid of revolution generated by revolving R(violet region) about the y-axis over the interval [1 , 3] Then the volume of the solid will be-
|
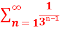 is convergent or divergent. Find its value in case of convergent.A20)The general formula for this series is given by,
is convergent or divergent. Find its value in case of convergent.A20)The general formula for this series is given by,Sn = We get,
Hence the series is convergent and its values is 3/2. Example-3: check whether the series Sol. The general formula can be written as,
We get on applying limits,
This is the convergent series and its value is 3 / 4 |
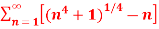 A21)
A21)
Here we take,
Which not zero and finite , So by comparison test ,
Is convergent. so that |
 A22)
A22)We have ,
Now , by D’Almbert ratio test At x = 1 , this test fails. Now , when x = 1
|
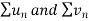 converges or diverges together.Since
converges or diverges together.Since 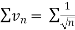 is the form of
is the form of 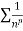 , in which
, in which 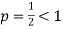 Hence
Hence  diverges then
diverges then  will also diverge.Therefore in the given series
will also diverge.Therefore in the given series  converges if x<1 and diverges if x≥1 Q23) If the series
converges if x<1 and diverges if x≥1 Q23) If the series  converges, then find the value of x.A23)
converges, then find the value of x.A23)Here Then,
By D’Almbert’s ratio test the series is convergent for |x|<1 and divergent if |x|>1. So at x = 1 The series becomes- At x = -1
|
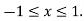 Q24) Expand
Q24) Expand 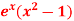 as far as the term in
as far as the term in 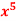 .A24)We know that the power series for
.A24)We know that the power series for 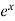 is-
is-
Here we have to find- So that-
On solving, we get-
|