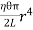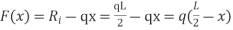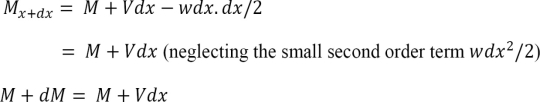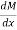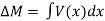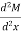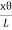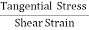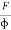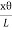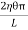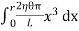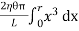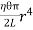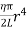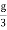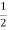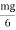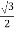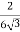The Tension of the wire is F= 4.0 X 3.1 π N. The area of cross-section is A= πr2 = π x (2.0 x 10-3 m)2 A = 4.0 π x 10-6 m2 Thus the tensile stress developed F/A = 4 X 3.1π / 4.0π x 10 N/m2 Stress = 3.1 x 106 N/m2
|
Young’s Modulus Y = FL/Al l = FL/AY = (5 x 3) /π x(0.5 x 10-3)2 x 120 x109 = 15.9 x 10-3 m
|
Given L = 1 m , r = 5 mm , ‖ = 450 = 45 x π /3600 η =200 X 109 Pa C = C= 54.056 Nm |
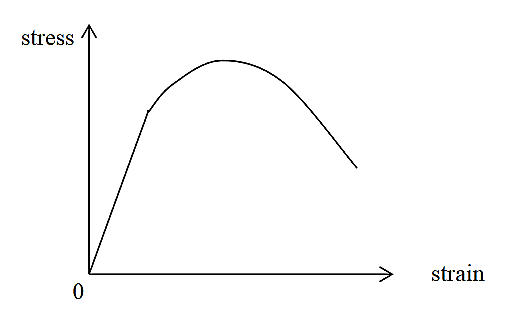
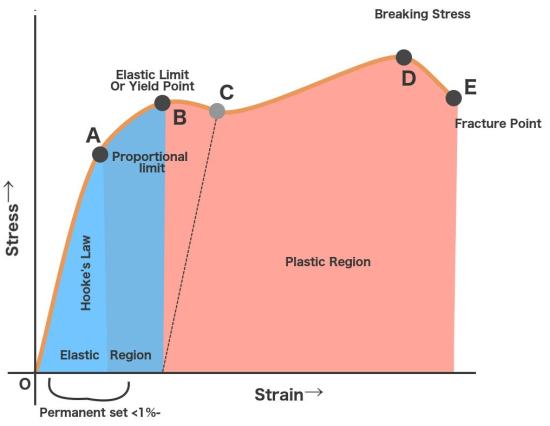
Hooke's Law In 17ᵗʰ century physicist Robert Hooke observed that the stress vs strain curve for many materials has a linear region.
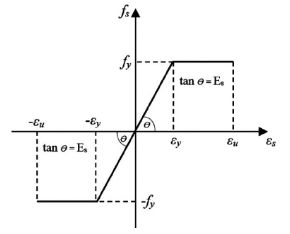
Hooke's law: Within the elastic limits, the strain produced in a body is directly proportional to the stress which causes it.
i.e., strain ∝ stress or stress ∝ strain
So
This constant is called 'modulus of elasticity. Hooks law can be defined as
The force required to stretch an elastic object such as a metal spring is directly proportional to the extension of the spring. This is known as Hooke's law and commonly written:
F=−kx
Where F is the force, x is the length of extension/compression k is a constant of proportionality known as the spring constant which is usually given in N/m.
Negative sign signify that the restoring force due to the spring is in the opposite direction to the force which caused the displacement.
Dimensional Formula [ML-1T-2]
The total length L of a spring under extension is equal to the nominal length L0 plus the extension x, L=L0+x and during compression of spring, it is given by L=L0 – x.
|
|
|
|
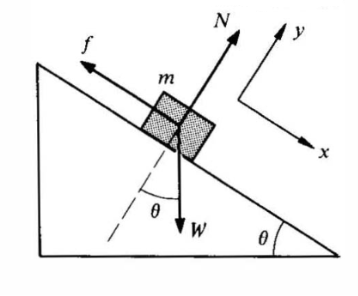
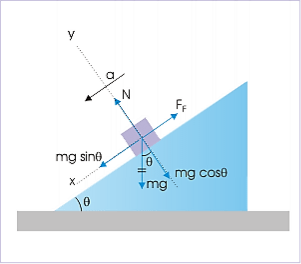
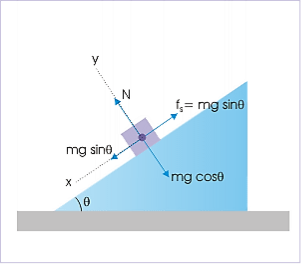
 = Wsinθ – fand m
= Wsinθ – fand m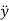 = N -Wcos
= N -Wcos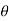 = 0. When sliding starts, f has its maximum value μN, and
= 0. When sliding starts, f has its maximum value μN, and 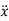 =0. The equations then giveWsinθmax = μNWcos
=0. The equations then giveWsinθmax = μNWcos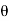 max = NHencetanθmax = μNotice that as the wedge angle is gradually increased from zero, the friction force grows in magnitude from zero toward its maximum value μN, since before the block begins to slide we havef = Wsinθ θ
max = NHencetanθmax = μNotice that as the wedge angle is gradually increased from zero, the friction force grows in magnitude from zero toward its maximum value μN, since before the block begins to slide we havef = Wsinθ θ θmax Q 13) A block of Mass M is moving with a velocity v on straight surface. What is the shortest distance and shortest time in which the block can be stopped if μ is coefficient of frictiona. v2/2μg,v/μg
θmax Q 13) A block of Mass M is moving with a velocity v on straight surface. What is the shortest distance and shortest time in which the block can be stopped if μ is coefficient of frictiona. v2/2μg,v/μgb. v2/μg,v/μg
c. v2/2Mg,v/μg
d none of the above
A 13) Force of friction opposes the motion
Force of friction=μN=μmg
Therefore retardation =μmg/m=μg
From v2=u2+2as
or
s=v2/2μg
from v=u+at
or t=v/μg Q 14) Write a note on fracture?A 14) Fracture is the separation of an object or material into two or more pieces under the action of stress. The fracture of a solid usually occurs due to the development of certain displacement discontinuity surfaces within the solid. If a displacement develops perpendicular to the surface of displacement, it is called a normal tensile crack or simply a crack; if a displacement develops tangentially to the surface of displacement, it is called a shear crack. Brittle fractures occur with no apparent deformation before fracture; ductile fractures occur when visible deformation does occur before separation.Fracture strength, also known as breaking strength, is the stress at which a specimen fails via fracture. This is usually determined for a given specimen by a tensile test, which charts the stress-strain curve. The final recorded point is the fracture strength.Bones, on the whole, do not fracture due to tension or compression. Rather they generally fracture due to sideways impact or bending, resulting in the bone shearing or snapping. The behaviour of bones under tension and compression is important because it determines the load the bones can carry.
|
|
|
|
|
|
|
|
|
|
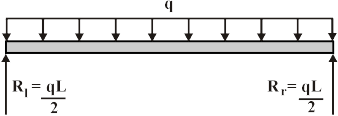
To compute the bending moment at section x + dx, use the following:
Or Equation (1) implies that the first derivative of the bending moment with respect to the distance is equal to the shearing force. The equation also suggests that the slope of the moment diagram at a particular point is equal to the shear force at that same point. Equation (1) suggests the following expression:
Equation (2) states that the change in moment equals the area under the shear diagram. Similarly, the shearing force at section x + dx is as follows: Vx+dx = V – wdx V + dV = V – wdx or
Equation (3) implies that the first derivative of the shearing force with respect to the distance is equal to the intensity of the distributed load. Equation (3) suggests the following expression:
Equation (4) states that the change in the shear force is equal to the area under the load diagram. Equation (1) and (3) suggest the following:
Equation (5) implies that the second derivative of the bending moment with respect to the distance is equal to the intensity of the distributed load.
|
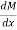 =0.
=0.
|
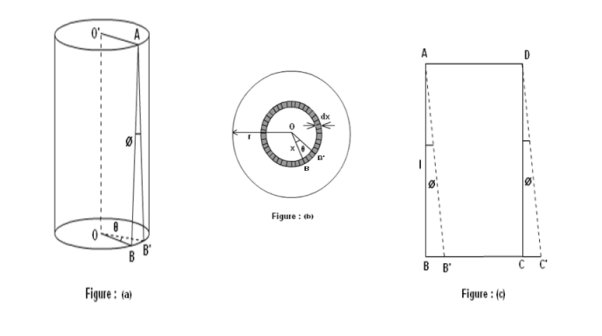
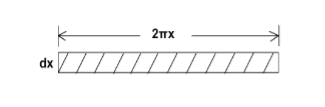
As shown in fig.(a), Let AB be the line parallel to the axis OO’ before twist produced and on twisted B shifts to B’, then line AB become AB’. Before twisting if hollow cylinder cut along AB and flatted out, it will form the rectangular ABCD as shown in fig.(c). But if it will be cut after twisting it takes the shape of a parallelogram AB’C’D. The angle of shear ∠BAB’ = ɸ From fig.(c) BB’= Lɸ From fig.(b) BB’= xθ So Lɸ= xθ And ɸ = The modules of rigidity is η = F = η ɸ = η The surface area of this hollow cylinder = 2πxdx
Figure 34: Hollow cylinder ∴ Total shearing force on this area = η = The moment of this force= = Now, integrating between the limits x = 0 and x = r, We have, total twisting couple on the cylinder = = = ∴ Total twisting couple = Then, the twisting couple per unit twist (θ= 1) is C = This twisting couple per unit twist is also called the torsional rigidity of the cylinder or wire.
|
|
|
|
|
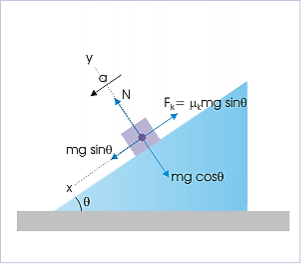
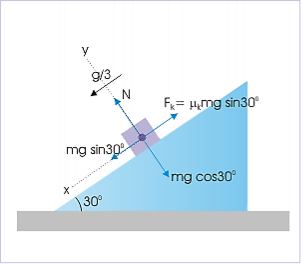
Motion on incline plane Motion of the block is opposed by kinetic friction. In the x-direction, ∑Fx = mgsin300−Fk =max ⇒ mgsin300− Fk =m ⇒mg ⇒Fk = mg In the y-direction, there is no acceleration, ∑Fy = mgcos300−N = 0⇒ N=mgcos300 = Putting values in the expression of coefficient of friction, we have: μk =
|