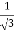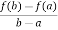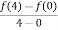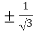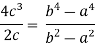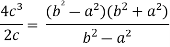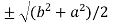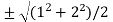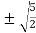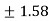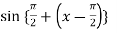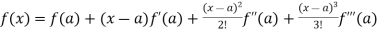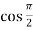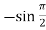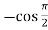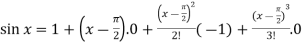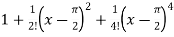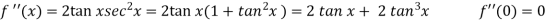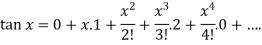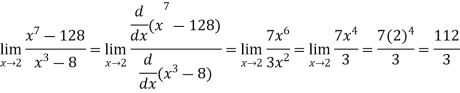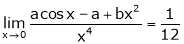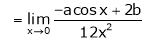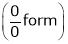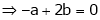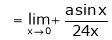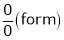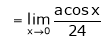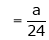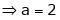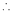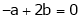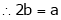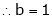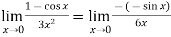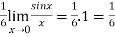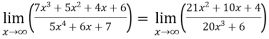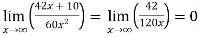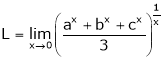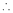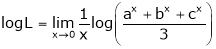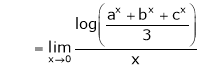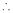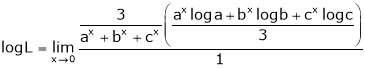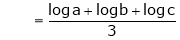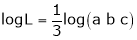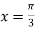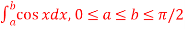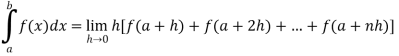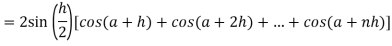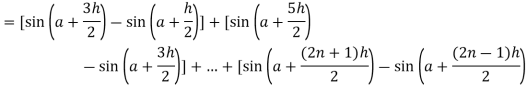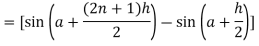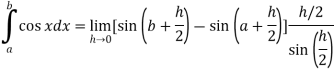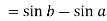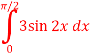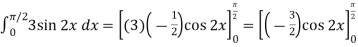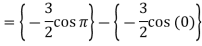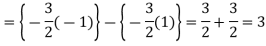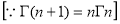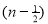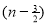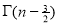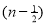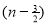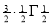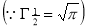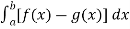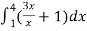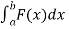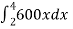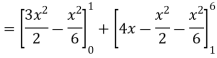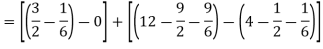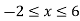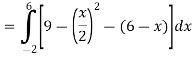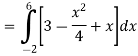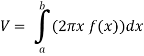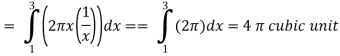1. f(x) = x³ - 6x²+11x-6 in the interval [1,3] 2. f(x) = x²-4x+8 in the interval [1,3] |
As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3] Also, f(1) = f(3) = 0 Now we find f’(x) = 0 3x² - 12x +11 = 0 We get, x = 2+ Hence both of them lie in (1,3). Hence the theorem holds good for the given function in interval [1,3]
(2) As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3] Also, f(1) = 1 -4 +8 = 5 and f(3) = 9 – 12 + 8 = 5 Hence f(1) = f(3) Now the first derivative of the function, f’(x) = 0 2x – 4 = 0 , gives X = 2 We can see that 1<2<3, hence there exists 2 between 1 and 3. And f’(2) = 0. This means that the Rolle’s theorem holds good for the given function and given interval. |
As we see that the given function is a polynomial and we know that the polynomial is continuous in [0,4] and differentiable in (0,4). f(x) = (x-1)(x-2)(x-3) f(x) = x-6x²+11x-6 now at x = 0, we get f(0) = -6 and at x = 4, we get. f(4) = 6 diff. the function w.r.t.x , we get f’(x) = 3x²-6x+11 suppose x = c, we get f’(c) = 3c²-6c+11 by Lagrange’s mean value theorem, f’(c) = now we get, 3c²-6c+11 = 3 3c²-6c+8 = 0 On solving the quadratic equation, we get C = 2 Here we see that the value of c lies between 0 and 4 Therefore the given function is verified. |
We are given, f(x) = x⁴ and g(x) = x Derivative of these fucntions , f’(x) = 4x³ and g’(x) = 2x put these values in Cauchy’s formula, we get
2c² = c² = c = now put the values of a = 1 and b = 2 ,we get c = Hence the Cauchy’s theorem is verified. |
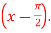 A4)
A4)Let f(x) = sin x Then, =
By using Taylor’s theorem-
Here f(x) = sin x and a = π/2
f’(x) = cosx , f’’(x) = - sin x , f’’’(x) = - cos x and so on.
Putting x = π/2 , we get f(x) = sin x = f’(x) = cos x = f’’(x) = -sin x = f’’’(x) = -cos x = from equation (1) put a =
= |
Let-
Put these values in Maclaurin’s series we get-
|
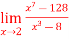 A6)
A6)Here we notice that it is an indeterminate form of So that , we can apply L’Hospital rule-
|
|
Let
But
|
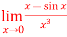 A8)
A8)We can see that this is an indeterminate form of type 0/0. Apply L’Hospital’s rule, we get
But this is again an indeterminate form, so that we will again apply L’Hospital’s rule- We get
|
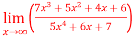 A9)
A9)Apply L’Hospital rule as we can see that this is the form of
Note- In some cases like above example, we can not apply L’Hospital’s rule. |
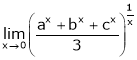 A10)
A10)Let
i.e.
|
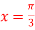 .A11)
.A11)Let
Then first derivative-
So that-
Now-
So that- So that-
Therefore f(x) has a maximum at |
|
Here we notice that f:x→cos x is a decreasing function on [a , b], Therefore by the definition of the definite integrals-
Then
Now,
Here Thus
|
|
|
|
= = = =
|
Here limits are given a = 1 , b = 4, We know that, area under the curve, A = = = = = (16 – 7/4) = 57/4 So that the area of the region is 57/4 unit square. |
Here, F = kx So that, 1200 = 2k K = 600 N/cm In that case, F = 600x We know that, W = W = W = 3600 N.cm |
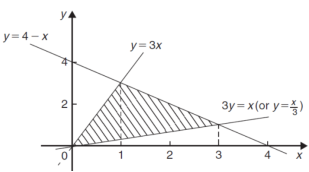
We get the following figure by using the equations of three straight lines- y = 4 – x, y = 3x and 3y = x
Area of shaded region-
|
|
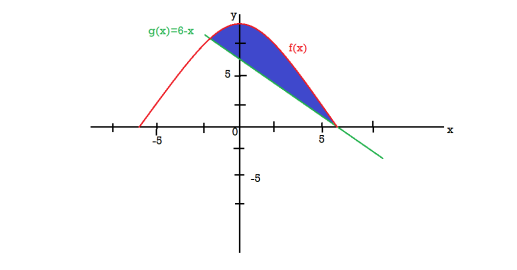
We get the following figure by using these two equations
To find the intersection points of two functions f(x) and g(x)- f(x) = g(x)
On factorizing, we get-
x = 6, -2 Now
Then, area under the curve- A =
Therefore the area under the curve is 64/3 square unit. |
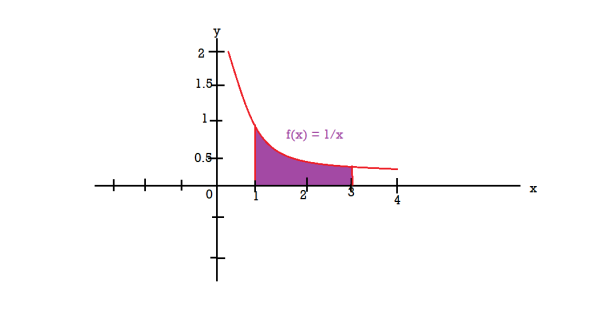
The graph of the function f(x) = 1/x will look like-
The volume of the solid of revolution generated by revolving R(violet region) about the y-axis over the interval [1 , 3] Then the volume of the solid will be-
|