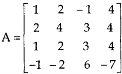
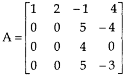
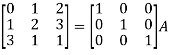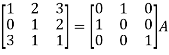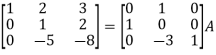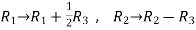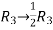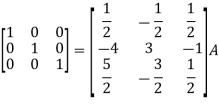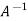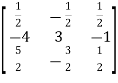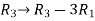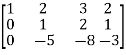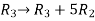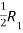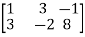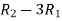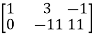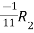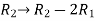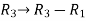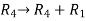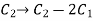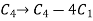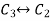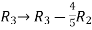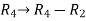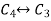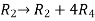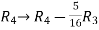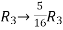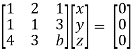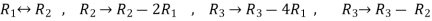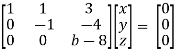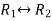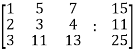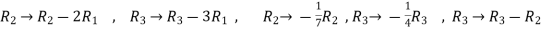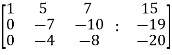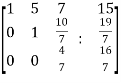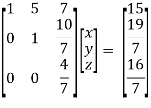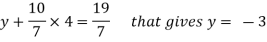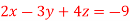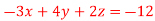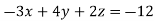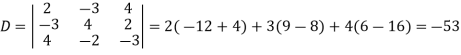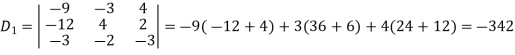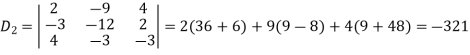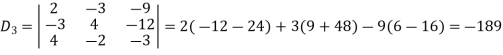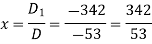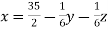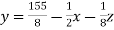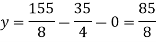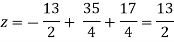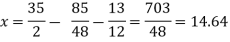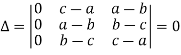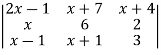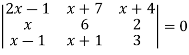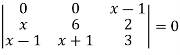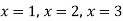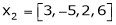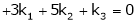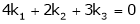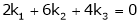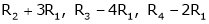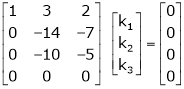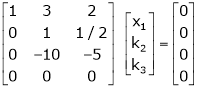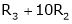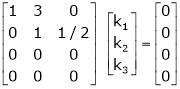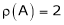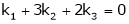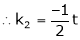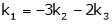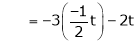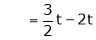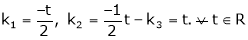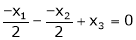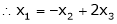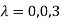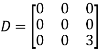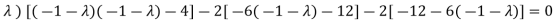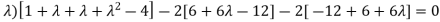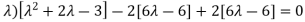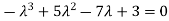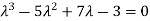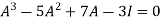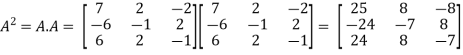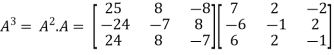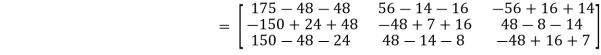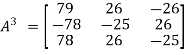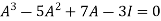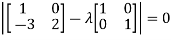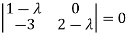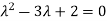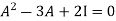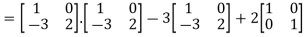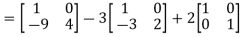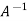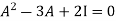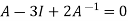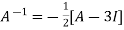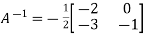A = |
Write the matrix ‘A’ as- A = IA
Apply
Apply
Apply
Apply
Apply
So that,
|
M = |
First we will convert the matrix M into echelon form, M = Apply, M = Apply M =
Apply M = We can see that, in this echelon form of matrix, the number of non – zero rows is 3. So that the rank of matrix X will be 3. |
A = |
Transform the matrix A into echelon form, then find the rank, We have, A = Apply, A = Apply A = Apply A = Apply A = Hence the rank of the matrix will be 2. |
|
We have,
We will apply elementary row operation,
We get,
Now apply column transformation,
We get,
Apply
Apply
Apply
Apply
Apply
As we can see this is required normal form of matrix A. Therefore, the rank of matrix A is 3. |
2x + y + 2z = 0 x + y + 3z = 0 4x + 3y + bz = 0 Which has (1) Trivial solution (2) Non-trivial solution |
For trivial solution, we already know that the values of x , y and z will be zerp, so that ‘b’ can have any value. Now for non-trivial solution- (2) Convert the system of equations into matrix form- AX = O
Apply
For non-trivial solutions, r(A) = 2 < n b – 8 = 0 b = 8 |
Re-write the system of equations in augmented matrix form. C = [A,B] That will be,
Apply
Now apply , We get,
Here rank of A = 3 And rank of C = 3, so that the system of equations is consistent, So that we can can solve the equations as below,
That gives, x + 5y + 7z = 15 ……………..(1) y + 10z/7 = 19/7 ………………(2) 4z/7 = 16/7 ………………….(3) From eq. (3) z = 4, From 2,
From eq.(1), we get x + 5(-3) + 7(4) = 15 That gives, x = 2 Therefore the values of x , y , z are 2 , -3 , 4 respectively. |
|
Here we have-
And here-
Now by using cramer’s rule-
|
The above equations can be written as,
Now put z = y = 0 in first eq. We get x = 35/2 put x = 35/2 and z = 0 in eq. (2) we have,
Put the values of x and y in eq. 3
Again start from eq.(1) By putting the values of y and z y = 85/8 and z = 13/2 We get
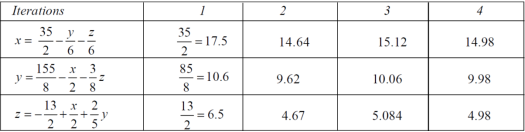
The process can be showed in the table format as below
At the fourth iteration , we get the values of x = 14.98 , y = 9.98 , z = 4.98 Which are approximately equal to the actual values, As x = 15 , y = 10 and y = 5 ( which are the actual values) |
|
Applying
We get,
Example: Solve-
Sol: given-
Apply-
We get-
|
Are the vectors |
Consider a vector equation,
i.e.
Which can be written in matrix form as,
Here
Put
Thus i.e. i.e.
Since F11k2, k3 not all zero. Hence |
 A10)
A10)Let A= The three Eigen vectors obtained are (-1,1,0), (-1,0,1) and (3,3,3) corresponding to Eigen values
Then Also we know that
|
A = |
Characteristic equation will be-
( 7 - (7- (7- Which gives,
Or
According to cayley-Hamilton theorem,
In order to verify cayley-Hamilton theorem , we will find the values of So that,
Now
Put these values in equation(1), we get
Hence the cayley-hamilton theorem is verified. |
|
Let A = The characteristics equation of A is
Or Or Or By Cayley-Hamilton theorem L.H.S:
= Multiply both side by
Or Or Or |