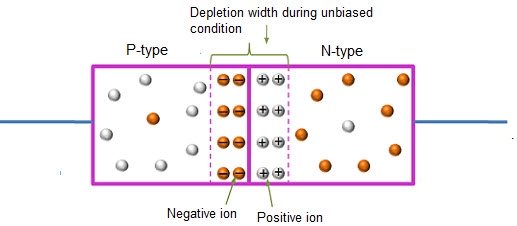
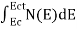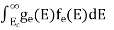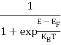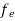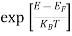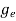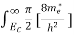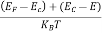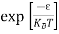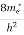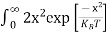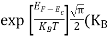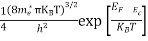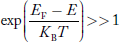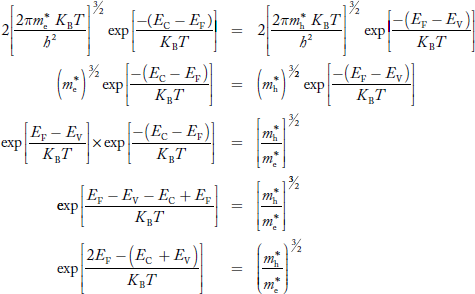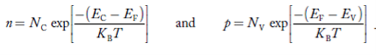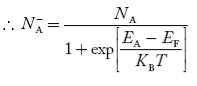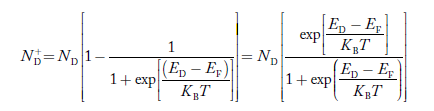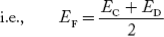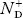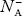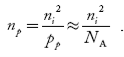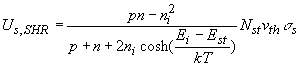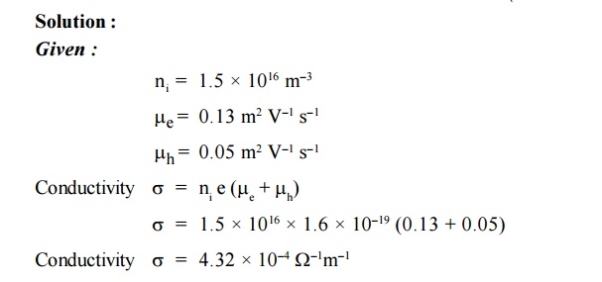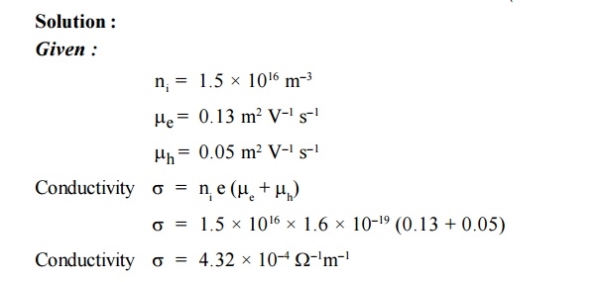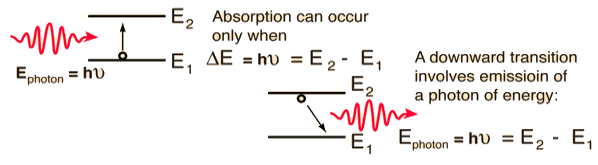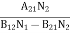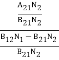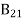| unit 3 semiconductors and light semiconductors interactions

PHY

UNIT-3SEMICONDUCTORS AND LIGHT- SEMICONDUCTOR INTERACTIONSQ1) Explain P-N Junction Diode and its I-V Characteristic? A1)Solution:A P-N Junction Diode is formed by doping one side of a piece of silicon with a P-type dopant (Boron) and the other side with a N-type dopant (phosphorus). Ge can be used instead of Silicon. The P-N junction diode is a two-terminal device. This is the basic construction of the P-N junction diode. It is one of the simplest semiconductor devices as it allows current to flow in only one direction.ZERO BIASED CONDITIONIn this case, no external voltage is applied to the P-N junction diode; and therefore, the electrons diffuse to the P-side and simultaneously holes diffuse towards the N-side through the junction, and then combine with each other. Due to this an electric field is generated by these charge carriers. The electric field opposes further diffusion of charged carriers so that there is no movement in the middle region. This region is known as depletion width or space charge.

Figure: Unbiased or zero biased PN Junction Diode

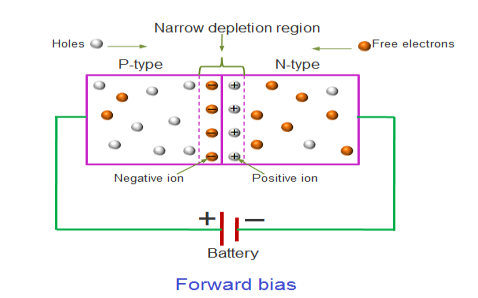
FORWARD BIASIn the forward bias condition, the positive terminal of the battery is connected to the P-Type material and the negative terminal of the battery is connected to the N-type material. This connection is also called as giving positive voltage.

Figure: Forward bias

Electrons from the N-region cross the junction and enters the P-region. Due to the attractive force that is generated in the P-region the electrons are attracted and move towards the positive terminal. Simultaneously the holes are attracted to the negative terminal of the battery. By the movement of electrons and holes current flows. In this condition, the width of the depletion region decreases due to the reduction in the number of positive and negative ions.If this external voltage Vf becomes greater than the value of the potential barrier, approx. 0.7 volts for silicon and 0.3 volts for germanium, the potential barriers opposition will be overcome and current will start to flow.This is because the negative voltage pushes or repels electrons towards the junction giving them the energy to cross over and combine with the holes being pushed in the opposite direction towards the junction by the positive voltage. This results in a characteristics curve of zero current flowing up to this voltage point, called the “knee” on the static curves and then a high current flow through the diode with little increase in the external voltage as shown in I-V characteristics.REVERSE BIASIn the reverse bias condition, the negative terminal of the battery is connected to the P-type material and the positive terminal of the battery is connected to the N-type material. This connection is also known as giving negative voltage.

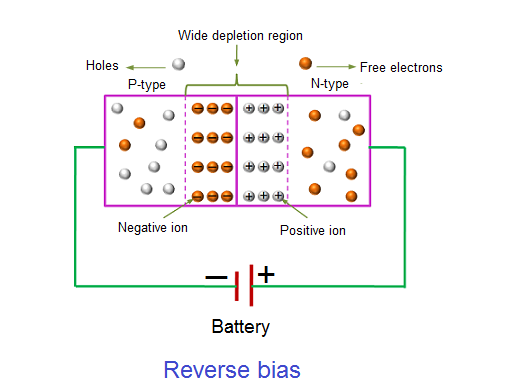
Figure: Reverse bias

The positive voltage applied to the N-type material attracts electrons towards the positive electrode and away from the junction, while the holes in the P-type end are also attracted away from the junction towards the negative electrode.The net result is that the depletion layer grows wider due to a lack of electrons and holes and presents a high impedance path, almost an insulator. The result is that a high potential barrier is created thus preventing current from flowing through the semiconductor material.This condition represents a high resistance value to the PN junction and practically zero current flows through the junction diode with an increase in bias voltage. However, a very small leakage current does flow through the junction which can be measured in micro-amperes, ( μA ).If the reverse bias voltage Vr applied to the diode is increased to a sufficiently high enough value, it will cause the diode’s PN junction to overheat and fail due to the avalanche effect around the junction. This may cause the diode to become shorted and will result in the flow of maximum circuit current, and this shown as a step downward slope in the reverse static characteristics curve in I-V characteristics.I-V CHARACTERISTICS OF PN JUNCTION DIODE The I-V Characteristic Curves, which is short for Current-Voltage Characteristic Curves or simply I-V curves of an electrical deviceThe application of a forward biasing voltage on the junction diode results in the depletion layer becoming very thin and narrow which represents a low impedance path through the junction thereby allowing high currents to flow. The point at which this sudden increase in current takes place is represented on the static I-V characteristics curve above as the “knee” point. The current starts increasing with increase in voltage. At knee voltage current shows a sharp increment in its magnitude. This behaviour is mentioned above. As large current flow in forward biasing so we measure this current in mA. When a junction diode is Reverse Biased, the thickness of the depletion region increases and the diode acts like an open circuit blocking current flow. So only a very small leakage current will flow.

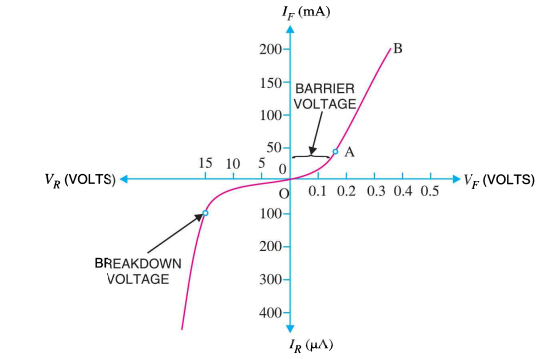
Figure: I-V characteristics

Q2) Discuss conduction in intrinsic semiconductor? A2)Solution:Intrinsic Semiconductor

An intrinsic type of semiconductor material made to be very pure chemically. As a result it possesses a very low conductivity level having very few number of charge carriers, namely holes and electrons, which it possesses in equal quantities.

The most commonly used semiconductor basics material by far is silicon. Silicon has four valence electrons in its outermost shell which it shares with its neighbouring silicon atoms to form full orbital’s of eight electrons. The structure of the bond between the two silicon atoms is such that each atom shares one electron with its neighbour making the bond very stable.

As there are very few free electrons available to move around the silicon crystal, crystals of pure silicon (or germanium) are therefore good insulators. Silicon atoms are arranged in a definite symmetrical pattern making them a crystalline solid structure. A crystal of pure silica (silicon dioxide or glass) is generally said to be an intrinsic crystal (it has no impurities) and therefore has no free electrons.

An extremely pure semiconductor is called as Intrinsic Semiconductor. On the basis of the energy band phenomenon, an intrinsic semiconductor at absolute zero temperature is shown below.

Its valence band is completely filled and the conduction band is completely empty. When the temperature is raised and some heat energy is supplied to it, some of the valence electrons are lifted to conduction band leaving behind holes in the valence band as shown below.

A hole is the absence of an electron in a particular place in an atom. Although it is not a physical particle in the same sense as an electron, a hole can be passed from atom to atom in a semiconductor material. It is considered to have positive charge. Holes are positive charge carriers.

The electrons reaching at the conduction band move randomly. The holes created in the crystal also free to move anywhere.

This behaviour of the semiconductor shows that they have a negative temperature coefficient of resistance. This means that with the increase in temperature, the resistivity of the material decreases and the conductivity increases.

But simply connecting a silicon crystal to a battery supply is not enough to extract an electric current from it. To do that we need to create a “positive” and a “negative” pole within the silicon allowing electrons and therefore electric current to flow out of the silicon. These poles are created by doping the silicon with certain impurities.

Q3) What is doping? Discuss its importance in semiconductor?A3)Solution:DopingThe process by which an impurity is added to a semiconductor is known as Doping. The amount and type of impurity which is to be added to a material has to be closely controlled during the preparation of extrinsic semiconductor. Generally, one impurity atom is added to a 108 atoms of a semiconductor.The purpose of adding impurity in the semiconductor crystal is to increase the number of free electrons or holes to make it conductive. If a Pentavalent impurity, having five valence electrons is added to a pure semiconductor a large number of free electrons will exist. Which make a n-type extrinsic semiconductor.If a trivalent impurity having three valence electrons is added, a large number of holes will exist in the semiconductor. Which make a p-type extrinsic semiconductor. Q4) What is P-type Extrinsic Semiconductor? Draw its energy level diagram and discuss the conduction mechanism in p type semiconductor? A4)Solution:P-type Extrinsic SemiconductorThe extrinsic p-Type Semiconductor is formed when a trivalent impurity is added to a pure semiconductor in a small amount, and as a result, a large number of holes are created in it. A large number of holes are provided in the semiconductor material by the addition of trivalent impurities like Gallium and Indium. Such type of impurities which produces p-type semiconductor are known as an Acceptor Impurities because each atom of them create one hole which can accept one electron.In a P-type semiconductor material there is a shortage of electrons, i.e. there are 'holes' in the crystal lattice. Electrons may move from one empty position to another and in this case it can be considered that the holes are moving. This can happen under the influence of a potential difference and the holes can be seen to flow in one direction resulting in an electric current flow. It is actually harder for holes to move than for free electrons to move and therefore the mobility of holes is less than that of free electrons. Holes are positively charged carriers.A trivalent impurity like Aluminium, having three valence electrons is added to Silicon crystal in a small amount. Each atom of the impurity fits in the Silicon crystal in such a way that its three valence electrons form covalent bonds with the three surrounding Silicon atoms as shown in the figure below.

Energy Band Diagram of p-Type SemiconductorThe energy band diagram of a p-Type Semiconductor is shown below.

A large number of holes or vacant space in the covalent bond is created in the crystal with the addition of the trivalent impurity. A small or minute quantity of free electrons is also available in the conduction band.They are produced when thermal energy at room temperature is imparted to the Silicon crystal forming electron-hole pairs. But the holes are more in number as compared to the electrons in the conduction band. It is because of the predominance of holes over electrons that the material is called as a p-type semiconductor. The word “p” stands for the positive material.

Conduction Through p Type SemiconductorIn p type semiconductor large number of holes are created by the trivalent impurity. When a potential difference is applied across this type of semiconductors.

The holes are available in the valence band are directed towards the negative terminal. As the current flow through the crystal is by holes, which are carrier of positive charge, therefore, this type of conductivity is known as positive or p type conductivity. In a p type conductivity the valence electrons move from one covalent to another.The conductivity of n type semiconductor is nearly double to that of p type semiconductor. The electrons available in the conduction band of the n type semiconductor are much more movable than holes available in the valence band in a p type semiconductor. The mobility of holes is poor as they are more bound to the nucleus.Even at the room temperature the electron hole pairs are formed. These free electrons which are available in minute quantity also carry a little amount of current in the p type semiconductors. Q5) For an intrinsic Semiconductor with a band gap of 0.7 eV, determine the position of EF at T = 300 K if m*h = 6m*eA5)Solution:

Q6) What is N-type Extrinsic Semiconductor? Draw its energy level diagram and discuss the conduction mechanism in N type semiconductor? A6)Solution:N-type Extrinsic SemiconductorWhen a few Pentavalent impurities such as Phosphorus whose atomic number is 15, which is categorised as 2, 8 and 5. It has five valence electrons, which is added to silicon crystal. Each atom of the impurity fits in four silicon atoms as shown in the figure below.Hence, each Arsenic atom provides one free electron in the Silicon crystal. Since an extremely small amount of Phosphorus, impurity has a large number of atoms; it provides millions of free electrons for conduction.

An N-type semiconductor material has an excess of electrons. In this way, free electrons are available within the lattices and their overall movement in one direction under the influence of a potential difference results in an electric current flow. This in an N-type semiconductor, the charge carriers are electrons.Energy Diagram of n-Type SemiconductorA large number of free electrons are available in the conduction band because of the addition of the Pentavalent impurity. These electrons are free electrons which did not fit in the covalent bonds of the crystal. However, a minute quantity of free electrons is available in the conduction band forming hole- electron pairs.The Energy diagram of the n-type semiconductor is shown in the figure below.

The addition of pentavalent impurity results in a large number of free electrons.

When thermal energy at room temperature is imparted to the semiconductor, a hole-electron pair is generated and as a result, a minute quantity of free electrons is available. These electrons leave behind holes in the valence band.

Here n stands for negative material as the number of free electrons provided by the pentavalent impurity is greater than the number of holes.

Conduction Through n-Type SemiconductorIn the n-type semiconductor, a large number of free electrons are available in the conduction bands which are donated by the impurity atoms. The figure below shows the conduction process of an n-type semiconductor.When a potential difference is applied across this type of semiconductor, the free electrons are directed towards the positive terminals. It carries an electric current. As the flow of current through the crystal is constituted by free electrons which are carriers of negative charge, therefore, this type of conductivity is known as negative or n-type conductivity.

The electron-hole pairs are formed at room temperature. These holes which are available in small quantity in valence band also consist of a small amount of current. For practical purposes, this current is neglected. Q7) Derive expression for carrier concentration for intrinsic semiconductors? Explain Fermi level for Intrinsic semiconductors and what is the effect of temperature on Fermi level?A7)Solution:Intrinsic semiconductors—carrier concentrationHere we will calculate the number of electrons excited into conduction band at temperature T and also the hole concentration in the valence band. It is assumed that the electrons in the conduction band behave as if they are free particles with effective mass me* and the holes near the top of the valence band behave as if they are free particles with effective mass mh*. Here we will calculate the electron concentration, hole concentrationDensity of Electrons in Conduction Band

The number of free electrons per unit volume of semiconductor having energies in between E and E + dE is represented as N(E) dE

dE = width of Energy band

Therefore, we have:

N(E) dE = ge(E) dE fe(E) ……….(1)

ge(E) = The density of electron states per unit volume

fe(E) = Fermi-Dirac distribution function i.e. probability that an electron occupies an electron state

The number of electrons present in the conduction band per unit volume of material ‘n’ is obtained by integrating N(E) dE between the limits Ec and Ect

Where Ec = the bottom energy levels of conduction band

Ect = the bottom and top energy levels of conduction band

n = ……….(2)

can be written as

n = =

n = - ……….(3)

we know that above Ect, there is no electrons.

Hence, Equation (3) becomes

n = -

n = ……….(4)

The Fermi-Dirac distribution function fe(E) can be represented as:

(E) = ……….(5)

Compared to the exponential value, so the ‘1’ in the denominator can be neglected.

So >>1

Hence, (E) = = ……….(6)

The density of electron states ge(E) in the energy space from E = 0 to E can be written as:

(E) = [ ]3/2 (E - 0) ½ ……….(7)

where me* is the effective mass of an electron and h is Planck’s constant.

(E)dE = [ ]3/2 (E - 0) ½dE ……….(8)

To evaluate n, the density of states is counted from Ec, since the minimum energy state in conduction band is Ec. so eq (8) can become

(E)dE = [ ]3/2 (E - Ec) ½dE ……….(9)

Substituting Equations (6) and (9) in (4) gives

n = 3/2 (E-)1/2dE

n = [ ]3/2 1/2dE ………… (10)

The above equation can be simplified by the following substitution:

Put ɛ = E − Ec ………… (11)

So, dɛ = dE

In Equation (11), Ec is constant, as we change the variable E to ε in Equation (10), the integral limits also change.

In Equation (11), as E → Ec then ε → 0 and E → ∞, then ε also → ∞.

the exponential term in Equation (10) becomes:

= exp [] = exp []

………… (12)

Substituting Equations (11) and (12) in (10), we get:

n = [ ]3/2 dE

n = [ ]3/2 dE ………… (13)

Above integral (I) can be simplified by substitution. Put ε = x2

so that dɛ = 2x dx

I =2x dx

=dx

= =T)3/2 ………… (14)

Substituting Equation (14) in (13) gives:

n = [ ]3/2T)3/2

n =

n = ………… (15)

The term is almost a constant compared with the exponential term as the temperature changes. So, it is a pseudo constant and is given by the symbol Nc. So, we have

n =Nc ………… (16)

Density of Holes in Valence BandThe number of holes per unit volume of semiconductor in the energy range E and E + dE in valence band is represented as P(E) dE. Proceeding same way( as in case of electrons) we have

Therefore, we have:

P(E) dE = gh(E) dE fh(E) ……….(17)

dE = width of Energy band

gh(E) = The density of holes states per unit volume

fh(E) = Fermi-Dirac distribution function i.e. probability that an hole occupies an electron state

The number of electrons present in the conduction band per unit volume of material ‘n’ is obtained by integrating P(E) dE between the limits Evb and EV

where EV = the bottom energy levels of valence band

Evb = the bottom and top energy levels of valence band

The total number of holes present in the valence band per unit volume of material ‘p’ is obtained by integrating P(E) dE

……….(18)

Equation (18) can be represented as:

……….(19)

Now we know that below Evb no holes is present. Hence, Equation (19) becomes

……….(20)

We know hole can also be defined as absence of an electron.

presence of a hole = the absence of an electron

Hence, the Fermi-Dirac function of holes fh(E) in the valence band is:

images

Compared to exponential, the ‘1’ in the denominator is negligible,

images

Hence,

……….(21)

The density of hole states between E and E + dE in valence band can be written similar to Equation (8.9) for electrons.

……….(22)

Where mh* is the effective mass of hole.

Substituting Equations (21) and (22) in (20),

……….(23)

The above equation can be simplified by the substitution:

Put ɛ = EV − E ............. (24)

so dɛ = − dE

In Equation (24), EV is constant, as we change the variable E to ε in Equation (23), the integral limits also change.

In Equation (24),

as E → EV then ε → 0

and E→ −∞, then ε → ∞

the exponential term in Equation (23) becomes:

............. (25)

Substituting Equations (24) and (25) in (23), we get:

………….(26)

From Equation (14), we know the integral value T)3/2 put here and we get

………….(27)

….The term is almost constant compared with the exponential term as the temperature changes. So, it is a pseudo constant and is given by the symbol NV. So, we have

…………… (28)

Q8) Explain Fermi level for Intrinsic semiconductors and what is the effect of temperature on Fermi level?A8)Solution:Fermi LevelWe know that in intrinsic semiconductor Electron concentration ‘n’ = Hole concentration ‘p’ Equating Equations (15) and (27), we get

images

Taking logarithms on both sides, we get

……………… (29)

Normally, mh* is greater than me*, since ln

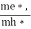is very small so that EF is just lie in the middle of energy gap Temperature effect on Fermi levelFermi level slightly rises with increase of temperature.But in case of pure intrinsic semiconductor like Si and Ge, mh* ≈ me* so in these cases Fermi level lies at the middle of energy gap. Q9) Calculate the intrinsic concentration of charge carriers at 300 K given that m *e =0.12m o ,m *h =0.28mo and the value of brand gap = 0.67 eV. A9) Solution:

Q10) Where Fermi level lie in case of p type and n type extrinsic semiconductor?Or Derive expression for Carrier Concentration in Extrinsic Semiconductors.A10)Solution:Carrier Concentration in Extrinsic SemiconductorsThe number of charge carriers present per unit volume of a semiconductor material is called carrier concentration. Suppose donor and acceptor atoms are doped in a semiconductor. At temperature T K,n = number of conduction electronsp = number of holes N−A = number of acceptor ions N+D = number of donor ions We know that the below equation hold good in semiconductor. The total negative charge due to conduction electrons and acceptor ions is equal to holes and donor ions in unit volume of material.So the material will be considered neutral if,n + N−A = p + N+D ……….(34) Equation (34) is called charge neutrality equation. In the above equation

………..(35)

concentration of acceptor ions N−A = acceptor concentration x probability of finding an electron in acceptor level

………..(36)

Similarly, the donor ions concentration is

………..(37)

In n-type material Note nn represents electrons in n-type material pn represents holes concentration in n-type material. there are no acceptor atoms so N−A = 0. At 0 K, all the electron states in donor level are occupied by electrons. As the temperature is increased from 0 K, some of the electrons jump from these donor states into the conduction band.Also the concentration of holes is extremely less compared with the concentration of conduction electrons [p << n]From Equation (34) we have

n = p N+D

(Or) n ≈ N+D …………(38) [since p << N+D]

At temperature T K,As the temperature increase Almost all the donor atoms donate electrons to conduction band.

So, in n-type material, the free electron concentration is almost equal to the donor atoms.

So we can rewrite the above equation as

nn ≈ ND …………….(39)

where nn represents electrons in n-type material

also the hole concentration in n-type material can be obtained by applying law of mass action nn pn =ni2

…………..(40)

where pn represents holes concentration in n-type material.

In n-type material at 0 K, the Fermi energy level lies in the middle of Ec and ED

images

At temperature> 0K

……….(41)

With increase in temperature the Fermi level shifts upwards according to Equation (61) slightly due to ionization of donor atoms. With further increase of temperature, electron-hole pairs are generated due to the breaking of covalent bonds, hence Fermi level shifts downwards.In p-type semiconductorNote

pp represents holes in p-type material

np represents electrons in p-type material

There are no donor atoms so means no ions present images = 0.

At 0 K, all the acceptor levels are not occupied by electrons.

As the temperature is increased from 0 K, some electrons jump from top valence band energy levels to the acceptor states, leaving holes in the valence band and acceptor ions images are formed.

At some room temperature T K, concentration of conduction electrons is extremely less compared with hole concentration.

∴ From Equation (34), we have

n + N−A = p ……………(42)

(or) N−A ≈ p ……………. (43) [since n << N−A]

At temperature T K, in p-type material,

the hole concentration is almost equal to the acceptor atoms in unit volume of the material.

So, Equation (43) can be written as

pp ≈ NA ……………….(44)

where pp represents holes in p-type material

The electron concentration in p-type material can be obtained by applying law of mass action as nppp = ni2

…………….(45)

where np represent free electron concentration in p-type material.

In p-type material, the Fermi level lies in between EV and EA at 0 K

As the temperature is increased from 0 K, the Fermi level shifts downwards slightly as per Equation (46) due to ionization of acceptor atoms. And with further increase of temperature, electron-hole pairs are generated due to the breaking of covalent bonds, so Fermi level shifts upwards.Q11) What is Recombination in semiconductor? Discuss any two different processes which lead to recombination?A11)Solution:Recombination is the reverse process where electrons from the conduction and holes from valence band recombine and are annihilated. These processes must conserve both quantized energy and momentum, and the vibrating lattice plays a large role in conserving momentum.

Recombination and generation are always happening in semiconductors both optically and thermally.

Their rates are in balance at equilibrium.

If the product of the rate becomes greater than the recombination rate, again driving the system back towards equilibrium.

As the electron and hole densities is a constant at equilibrium, maintained by recombination and generation occurring at equal rates.

When there is a surplus of carriers the rate of recombination becomes greater than the rate of generation, driving the system back towards equilibrium.

In semiconductors several different processes exist which lead to recombination, the most important ones are: 1) Band-to-band recombination2) Auger generation/recombination3) Surface recombination Note- You can discuss any two out of three.1) Band-to-band recombination or Radiative recombinationBand-to-band recombination or Radiative recombination is the reverse process of photon absorption, where an electron drops back down to its equilibrium energy band and radiates a photon.It is the process of electrons jumping down from the conduction band to the valence band in a radiative manner. During band-to-band recombination the energy absorbed by a material is released in the form of photons. Generally, these released photons contain the same or less energy than those initially absorbed.The photon emitted may have the energy of the band gap difference or less, depending on how much energy is lost in the mechanismRadiative recombination plays a more major role in direct band semiconductors.The total radiative recombination rate, given below as R, is proportional to the product of the concentration of occupied states (electrons, n) in the conduction band and that of the unoccupied states in the valence band (holes, p)R= BnpBand-to-band recombination depends on the density of available electrons and holes. Both carrier types need to be available in the recombination process. Therefore, the rate is expected to be proportional to the product of n and p. Also, in thermal equilibrium, the recombination rate must equal the generation rate since there is no net recombination or generation. As the product of n and p equals ni2 in thermal equilibrium, the net recombination rate can be expressed as:U= B(np-ni2)where B is the bimolecular recombination constant for a given semiconductor. It can be calculated from the semiconductor’s absorption coefficient. ni2 is the familiar “intrinsic carrier concentration”Auger recombinationAuger recombination involves three particles: an electron and a hole, which recombine in a band-to-band transition and give off the resulting energy to another electron or hole. The expression for the net recombination rate is therefore similar to that of band-to-band recombination but includes the density of the electrons or holes, which receive the released energy from the electron-hole annihilation.In other words Auger recombination the energy is given to a third carrier which is excited to a higher energy level without moving to another energy band. After the interaction, the third carrier normally loses its excess energy to thermal vibrations. Since this process is a three-particle interaction, it is normally only significant in non-equilibrium conditions when the carrier density is very high. Auger recombination is most important at high carrier concentrations caused by heavy doping. In silicon-based solar cells, Auger recombination limits the lifetime and ultimate efficiency. The more heavily doped the material is, the shorter the Auger recombination lifetime. Surface recombination Recombination at surfaces and interfaces can have a significant impact on the behavior of semiconductor devices. Areas of defect, such as at the surface of solar cells where the lattice is disordered, recombination is very high.This is because surfaces and interfaces typically contain a large number of recombination centers because of the abrupt termination of the semiconductor crystal, which leaves a large number of electrically active states. In addition, the surfaces and interfaces are more likely to contain impurities since they are exposed during the device fabrication process. The net recombination rate due to trap-assisted recombination and generation is given by:

the recombination is due to a two-dimensional density of traps, Nts, as the traps only exist at the surface or interface.Understanding the impacts and the ways to limit surface recombination leads to better and more robust solar cell designs. Surface recombination is high in solar cells, but can be limited. Q12) The intrinsic carrier density is 1.5 × 1016 m–3. If the mobility of electron and hole are 0.13 and 0.05 m2 V–1 s–1, calculate the conductivity.A12)

Q13) What is Drift current and diffusion currents? Derive expression for total hole and total electron current? A13)Solution:In case of semiconductors we observe two kinds of currents.

Drift current

Diffusion current

Drift current Definition: The flow of electric current due to the motion of charge carriers under the influence of external electric field is called drift current. When an electric field E is applied across a semiconductor material, the charge carriers attain a drift velocity vdSo drift velocity vd =μ .E

The relation between current density J and drift velocity vd is

J = Nqvd

Where N is the carrier concentration

q is the charge of electron or hole

From equations (1) and (2), we get

Jdrift = Nq μE

μ is the mobility of charge carrier.

The above equation shows the general expression for drift current density. Drift current density due to electrons is

Je(drift) = neμeE

Where n is the electrons carrier concentration

and μe is the mobility of electrons.

Drift current density due to holes is

Jh(drift) = peμhE

Where p is the carrier concentration of holes.

μh is the mobility of holes

so Total drift current density

Jdrift (total) = Je(drift) + Jh(drift) = neμeE + peμhE

= eE (nμe+pμh )

Diffusion current Definition: The flow of electric current due to the motion of charge carriers under concentration gradient is called diffusion current Or The motion of charge carriers from the region of higher concentration to lower concentration leads to a current called diffusion current. Let ∆N be the excess electron concentration. Then according to Fick’s law, the rate of diffusion of charge carriers is proportional to concentration gradient

Rate of diffusion of charge ∝ -

= - D

Where D is the diffusion coefficient of charge carriers.

The negative sign indicates decrease of N with increase of x So,

the diffusion current density Jdiffu is

Jdiffu = - qD

Where q is the charge of the charge carrier

Diffusion current density due to holes is

Jdiffu (hole) = - eDh

Diffusion current density due to electrons is (as electron carry negative charge so we will get +sign here.

Jdiffu (electrons) = eDe

Jdiffu (total) = Jdiffu (hole) + Jdiffu (electrons)

Jdiffu (total) = - eDh + eDe

The expression for total current density due to holes is

Jh (total) = Jh(drift) + Jdiffu (hole) = peμhE - eDh

The expression for total current density due to electrons is

Je (total) = Je(drift) + Jdiffu (electrons) = neμeE + eDe

Q14) The intrinsic carrier density is 1.5 × 1016 m–3. If the mobility of electron and hole are 0.13 and 0.05 m2 V–1 s–1, calculate the conductivity.A14)

Q15) Discuss Optical Transitions in Bulk Semiconductors?A15) Solution:

In semiconductors electrons can make transitions between two energy states and generate or destroy photons in the process.

In particular, transitions between the conduction band (EC) and the valence band ( EV) are optically active.

As the lower conduction band generally consists of s-like states while the upper valence band contains of p-like states.

Spontaneous emission, absorption, and stimulated emission can all take place between conduction band (EC) states and valence band (EV) states.

Absorption

Similar to stimulated absorption in optics in the semiconductor absorption all we need is an incoming photon, a valence band energy state occupied by an electron, and an empty conduction band energy state.

We know that in equilibrium condition, the valence band is fully occupied and the conduction band is empty.

We know that for optical absorption between two states in an atom only occurred for a narrow spectrum of photon energies so here in optical absorption in a semiconductor can occur over a wide range of photon energies.

This process carry out when the energy photon is greater than or equal to the band gap energy.

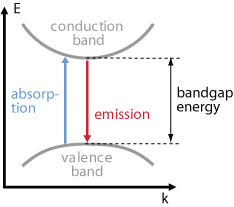
Figure: Band gap energy diagram

Incoming photon interacts with electron in valence band and provides it sufficient energy for excitation and by getting enough energy the electron jump to conduction band and leaving hole in valence band.

The absorption process creates an electron in the conduction band and a hole in the valence band, it is also called optical generation.

If the electrons created at energies higher than the band edge will quickly stabilize to the lowest conduction band energy states by releasing phonons.

Holes created deep in the valence band will ‘float up’ to the valence band edge.

Spontaneous Emission

Consider the system is in equilibrium but temperature is increased let us consider it is at T temperature.

Electrons and holes can be created by optical absorption and other pumping mechanisms.

The spontaneous emission process is possible for a wide range of photon energies above the band gap similar to absorption.

At T temperature the lowest energy states are mostly full in conduction band.

At T temperature the highest energy states are mostly empty in valence band.

Therefore, the spontaneous emission observed in semiconductor in which photon has energy nearly equal to the band gap energy.

Since the spontaneous emission process ‘destroys’ an electron and a hole, it is also called spontaneous optical recombination.

Stimulated emission

The stimulated emission process ‘destroys’ an electron and a hole, it is also called stimulated optical recombination.

In order to make stimulated emission the dominant optical process, we need to achieve population inversion.

It is the most important process for laser operation.

In this process a copy of the incoming photon is produced.

we expect that in most cases the stimulated emission will occur primarily between band-edge states, as these states are most likely to be occupied with electrons and holes just like in spontaneous emission.

Semiconductor optical amplifiers generally amplify light whose photon energy is approximately equal to the band gap energy of the semiconductor gain medium.

Figure: Absorption or gain, spontaneous emission and stimulated emission.

In thermal equilibrium, a direct-band-gap semiconductor (e.g., GaAs, InP, or GaSb) has a few electrons in the conduction band and a few holes (empty electron states) in the valence band. When a photon of energy greater than the band gap passes through such a semiconductor, the photon has a high probability of being absorbed, giving its energy to an electron in the valence band, thereby raising the electron to the conduction band. In principle, such a photon could stimulate the emission of an identical photon with the transition of an electron from the conduction to the valence band. The emitted photon derives its energy from the energy lost by the electron. In thermal equilibrium the number of electrons in the conduction band is very small, so the probability of stimulated emission is negligible compared to the probability for absorption. However, external excitation, can sufficiently increase the number of electrons in the conduction band such that the probability of stimulated emission eventually becomes higher than the probability of absorption. This situation corresponds to population inversion in a laser medium and is necessary for optical gain. The external excitation which generates a high density of electron-hole pairs in a semi-conductor is usually provided by current injection. It can also be achieved by optical pumping (absorption of radiation higher in energy than the band gap). Q16) Why ordinary silicon is not useful for light emission? Or Why stimulated emission process is not carrying out in indirect band gap semiconductors?A16) Solution: Silicon has an indirect band gap. That means that the lowest energy states in the conduction band have a different momentum than the highest energy states in the valence band. As we discussed above At T temperature the lowest energy states are mostly full in conduction band and the highest energy states are mostly empty in valence band. So these are the states that are most likely to be occupied by an electron and a hole. The spontaneous emission process must conserve both energy and momentum, but photons carry very little momentum but it is not zero have some finite value.Therefore, an electron at the ‘bottom’ of the conduction band is unable to recombine with a hole at the ‘top’ of the valence band via spontaneous photon emission, because that would violate conservation of momentum: the electron would have to undergo a significant momentum change, and the photon is unable to carry away enough momentum. This is the reason ordinary silicon is not useful for light emission and stimulated emission process is not carrying out in indirect band gap semiconductors. Q17) Differentiate between spontaneous and stimulated emissions.A17)

Spontaneous emission	Stimulated emission
1.The spontaneous emission was postulated by Bohr	1.The stimulated emission was postulated by Einstein
2. Additional photons are not required in spontaneous emission	2. Additional photons are required in stimulated emission
3.One photon is emitted in spontaneous emission	3.Two photons are emitted in stimulated emission
4.The emitted radiation is poly-monochromatic	4.The emitted radiation is monochromatic
5. The emitted radiation is Incoherent	5. The emitted radiation is Coherent
6. The emitted radiation is less intense	6. The emitted radiation is high intense
7.The emitted radiation has less directionality	7.The emitted radiation has high directionality
8. Example: light from sodium or mercury lamp	8. Example: light from the laser source.

Q18) What is LASER? Discuss basic phenomena involved in producing laser light?A18) LASER stands for “Light Amplification by Stimulated Emission of Radiation”.L = LightA = Amplification (by)S = StimulatedE = Emission (of)R = Radiation Theodore H. Maiman of the Hughes Research Laboratory, California, was the first scientist who experimentally demonstrated laser by flashing light through a ruby crystal in 1960. But the basic idea behind the development of laser was given by the great scientist “Albert Einstein” in 1917. Let us discuss Einstein’s theory of the interaction of electromagnetic radiation with matter. He proposed that electromagnetic radiation interacts with matter in the following three steps.

Stimulated Absorption

Spontaneous Emission

Stimulated Emission

Stimulated Absorption: Let E1 and E2 be the energies of the ground and excited states of an atom. Suppose, if a photon of energy hν= E1− E2 interacts with an atom present in the ground state, the atom gets excitation from ground state E1 to excited state E2. This process is called stimulated absorption. Stimulated absorption rate depends upon the number of atoms available in the lowest energy state as well as the energy density photons. Stimulated absorption rate ∝ Number of atoms in the ground state∝ The density of photons Spontaneous emission

Spontaneous Emission: Let E1 and E2 be the energies of the ground and excited states of an atom. Suppose, if a photon of energy hν= E1− E2 interacts with an atom present in the ground state, the atom gets excitation from ground stateE1 to excited state E2. The excited atom does not stay a long time in the excited state. The excited atom gets de-excitation after its lifetime by emitting a photon of energy hν= E1− E2. This process is called spontaneous emission. Also Spontaneous means by its own. Here excited atom comes to the ground state on its own so it is named as spontaneous emission. The spontaneous emission rate depends upon the number of atoms present in the excited state. Spontaneous emission ∝ rate number of atoms in the excited state Stimulated Emission: This phenomenon is responsible for producing laser light. Let E1and E2 be the energies of the ground and excited states of an atom. Suppose, if a photon of energy hν= E1− E2 interacts with an atom present in the ground state, the atom gets excitation from ground stateE1 to excited state E2. Let, a photon of energy hν= E1− E2 interacts with the excited atom within their lifetime; the atom gets de-excitation to the ground state by emitting another photon. These photons have the same phase and it follows coherence. This phenomenon is called stimulated emission. Stimulated emission rate depends upon the number of atoms available in the excited state as well as the energy density of photons. Stimulated emission rate ∝ number of atoms in the excited state ∝ Density of photons Q19) Derive Einstein’s coefficient A and B? A19) The distribution of atoms in the two energy levels will change by absorption or emission of radiation. Einstein introduced three empirical coefficients to quantify the change of population of the two levels. Let N1 be the number of atoms per unit volume with energy E1 and N2 be the number of atoms per unit volume with energy E2. Let ‘n’ be the number of photons per unit volume at frequency ‘υ’ such that hυ= E1− E2. Then, the energy density of photons ρ(υ) = nhυ

Description: http://hyperphysics.phy-astr.gsu.edu/hbase/imgmod/qpro1.gif

When these photons interact with atoms, both upward (absorption) and downward (emission) transition occurs. At the equilibrium, the upward transitions must be equal to downward transitions.Upward Transition Stimulated absorption rate depends upon the number of atoms available in the lowest energy state as well as the energy density photons.

We have seen above that

Stimulated absorption rate ∝ N1 i.e. Number of atoms in the ground state

∝ ρ(υ) i.e. Density of photons spontaneous emission

Stimulated absorption rate = B12N1ρ(υ) ………(1)

Where B12 is the Einstein coefficient of stimulated absorption.Downward transition The spontaneous emission rate depends upon the number of atoms present in the excited state.

Spontaneous emission rate ∝ N2 i.e. number of atoms in the excited state

Spontaneous emission rate = A21N2 ………(2)

Where A21 is the Einstein coefficient of spontaneous emission.

Stimulated emission rate depends upon the number of atoms available in the excited state as well as the energy density of photons.

Stimulated emission rate ∝ N2 i.e. number of atoms in the excited state

∝ ρ(υ) i.e. Density of photons

Stimulated emission rate = B21N2ρ(υ) ………(3)

if the system is in equilibrium the upward transitions must be equal to downward transitions.

upward transitions = downward transitions

B12N1ρ(υ) = A21N2 + B21N2ρ(υ) ………(4)

B12N1ρ(υ) - B21N2ρ(υ) = A21N2

(B12N1- B21N2) ρ(υ) = A21N2

ρ(υ) = ………(5)

Divide with B21N2 in numerator and denominator in the right side of the above equation,

ρ(υ) = = ………(6)

ρ(υ) = = = ………(7)

We know from Maxwell Boltzmann distribution law

= ………(8)

And also from Planck’s law, the radiation density

ρ(υ) = ………(9)

Comparing the two equations (7) and (9)

= and =1 ………(10)

The above relations are referred to as Einstein relations.

From the above equation for non-degenerate energy levels, the stimulated emission rate is equal to the stimulated absorption rate at the equilibrium condition.

= ………(11)

Q20) What is the relationship between B21 and B12?
a) B12 > B21
b) B12 < B21
c) B12 = B21
d) No specific relation
A20)C is the correct answer.
B21 is the coefficient for the stimulated emission while B12 is the coefficient for stimulated absorption. Both the processes are mutually reverse processes and their probabilities are equal. Therefore, B12 = B21. Q21) What is Pumping? Discuss the various type of pumping mechanisms? A21)Solution: For laser action, the pumping mechanism (exciting with external source) maintain a higher population of atoms in the upper energy level relative to that in the lower level.A system in which population inversion is achieved is called an active system. The method of raising the particles from a lower energy state to a higher energy state is called pumping. The process of achieving population inversion is called pumping. This can be done in several ways. The most commonly used pumping methods are

Optical pumping

Electrical discharge pumping

Chemical pumping

Thermal Pumping

Injection current pumping

Inelastic Atom-Atom Collisions

Optical pumping As the name suggests, in this method, light is used to supply energy to the laser medium. Optical pumping is used in solid laser. Xenon flash tubes are used for optical pumping. Since these materials have very broadband absorption, a sufficient amount of energy is absorbed from the emission band of the flash lamp and population inversion is created. So xenon flash lamp is used to produce more electrons in the higher energy level of the laser medium. Examples of optically pumped lasers are ruby, Nd: YAG Laser(Neodymium: Yttrium Aluminum Garnet). Electrical discharge pumping is used in gas lasers. Since gas lasers have a very narrow absorption band pumping then any flash lamp is not possible. Electric discharge refers to the flow of electrons or electric current through a gas, liquid, or solid. In this method of pumping, electric discharge acts as the pump source or energy source. A high voltage electric discharge (flow of electrons, electric charge, or electric current) is passed through the laser medium or gas. The intense electric field accelerates the electrons to high speeds and they collide with neutral atoms in the gas. As a result, the electrons in the lower energy state gains sufficient energy from external electrons and jumps into the higher energy state Examples of Electrical discharge pumped lasers are He-Ne laser, CO2 laser, argon-ion laser, etc. Chemical pumping Chemical reaction may also result in excitation and hence the creation of population inversion in a few systems. If an atom or a molecule is produced through some chemical reaction and remains excited at the time of production, then it can be used for pumping. The hydrogen fluoride molecule is produced in an excited state when hydrogen and fluorine gas chemically combine. The number of produced excited atoms or molecules is greater than the number of normal state atoms or molecules. Thus, population inversion is achieved. Examples H2 + F2 → 2HF, in this chemical reaction, hydrogen (H2) and fluorine (F2) molecules are chemically combined to produce hydrogen fluoride molecule (2HF) in an excited state.Thermal Pumping: Sometimes we can achieve population inversion by heating the laser medium. In thermal pumping, heat acts as the pump source or energy source. In this method, population inversion is achieved by supplying heat into the laser medium.When heat energy is supplied to the laser medium, the lower energy state electrons gain sufficient energy and jumps into the higher energy level. The process of achieving population inversion in thermal pumping is almost similar to the optical pumping or electric discharge method, except that in this method heat is used as a pump source instead of light or electric discharge.Injection current pumping In semiconductors, injection of current through the junction results in creates of population inversion among the minority charge carriers.Examples of such systems are InP and GaAs.Inelastic Atom-Atom Collisions: Like the electric discharge method, here also a high voltage electric discharge acts as a pump source. However, in this method, a combination of two types of gases, say X and Y are used. The excited state of gas X is represented as X+ whereas gas Y is represented as Y+. Both X and Y gases have the same excited states (X+ and Y+).When high voltage electric discharge passes through a laser medium having two types of gases X and Y, the lower energy state electrons in gas X will move to the exciting state X+ similarly the lower energy state electrons in gas Y moves to the excited state Y+. Initially, during electric discharge, the lower energy state electrons in gas X or atom X gets excited to X+ due to continuous collision with electrons. The excited state electrons in gas X+ now collide with the lower energy state electrons in gas Y. As a result, the lower energy state electrons in gas Y gains sufficient energy and jump into the exciting state Y+. This method is used in the Helium-Neon (He-Ne) laser.

Sign Up