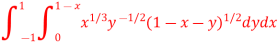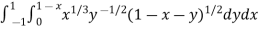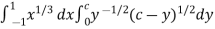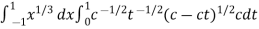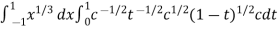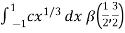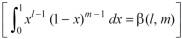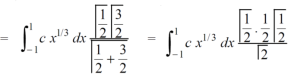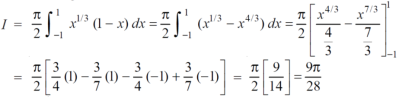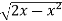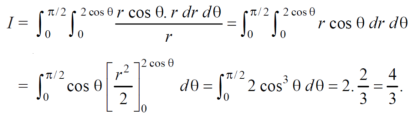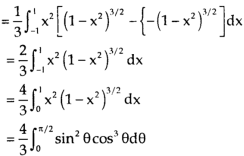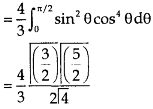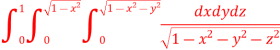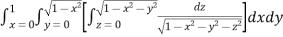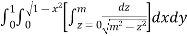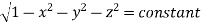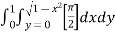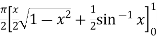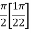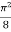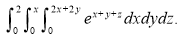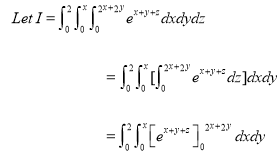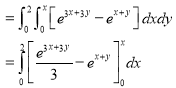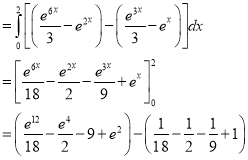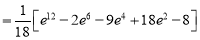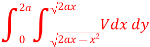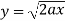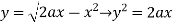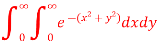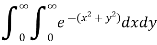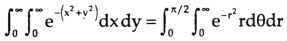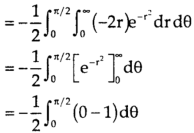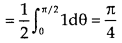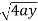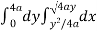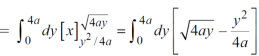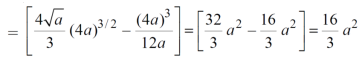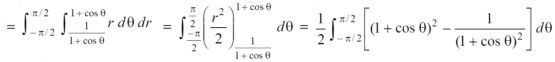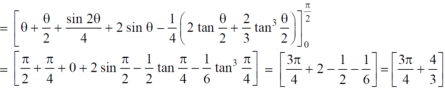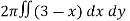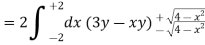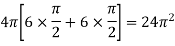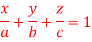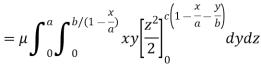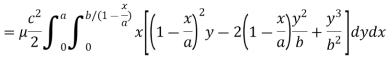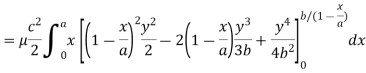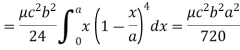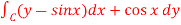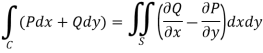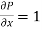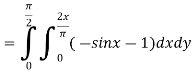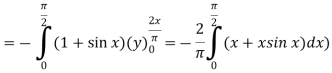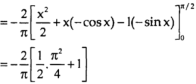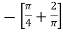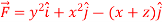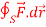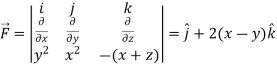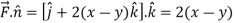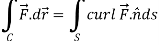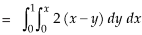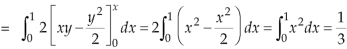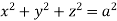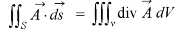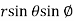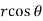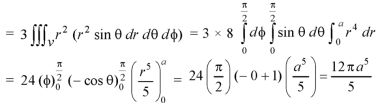|
Let us suppose the integral is I, I = Put c = 1 – x in I, we get I = Suppose, y = ct Then dy = c now we get, I = I = I = I = I = As we know that by beta function,
Which gives,
Now put the value of c, we get
|
|
In this problem, the limits for y are 0 to Suppose, y = squaring both sides, y² = 2x - x² x² + y² = 2x but in polar coordinates, we have, r² = 2r cosθ r = 2 cosθ
from the region of integration, r lies from 0 to 2 cosθ and θ varies from 0 to π / 2. As we know in case of polar coordinates, Replace x by r cosθ and y by r sinθ, dy dx by r drdθ, We get,
|
|
Let the integral, I = =
Put x = sinθ
= π / 24 ans.
|
|
Let I = = (Assuming m = = = = = = = = I = |
|
|
|
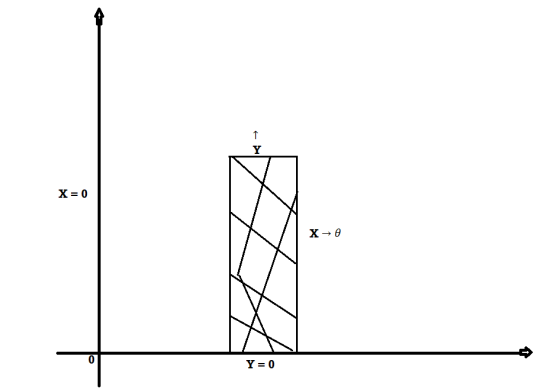
Limits are given- x = 0, x = 2a
And
and
The area of integration is the shaded portion of OAB. On changing the order of integration first we will integrate with respect to x, the area of integration has three portions BCE, ODE and ACD,
Now-
Which is the required answer.
|
|
We have
The limits of x and y are 0 to Hence the region of integration is in the first quadrant,
The region is covered by the radius strip from r = 0 to r = ∞ and it starts from θ = 0 to θ = π/2 Hence the integral becomes-
|
Let, y² = 4ax ………………..(1) and x² = 4ay…………………..(2) then if we solve these equations , we get the values of points where these two curves intersect
x varies from y²/4a to now using the conceot of double integral, Area =
|
Let, r = 1 + cosθ ……………………..(1) r(1 + cosθ) = 1……………………..(2) solving these equations, we get (1 + cosθ )(1 + cosθ ) = 1 (1 + cosθ )² = 1 1 + cosθ = 1 cosθ = 0 θ = ±π / 2 so that, limits of r are, 1 + cosθ and 1 / 1 + cosθ The area can be founded as below,
|
We know that, Volume = Here , PQ = 3 – x, =
The volume is 24π². |
|
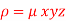 A11:
A11:
Here we the mass will be-
The limits of y are from y = 0 to y = b(1 – x/a) and limits of x are from 0 to a.
Therefore the required mass will be-
Which is the required answer. |
|
First we will draw the figure-
Here the vertices of triangle OED are (0,0), ( Now by using Green’s theorem-
Here P = y – sinx, and Q =cosx So that-
Now-
= Which is the required answer. |
If |
here we see that z-coordinates of each vertex of the triangle is zero, so that the triangle lies in the xy-plane and Now, Curl Curl
The equation of the line OB is y = x Now by stoke’s theorem,
|
|
Where-
And S is the surface of the sphere Sol.
On putting x =
|