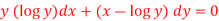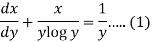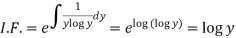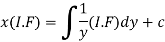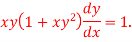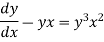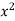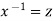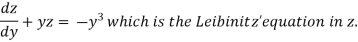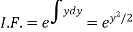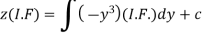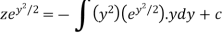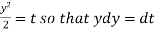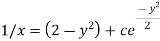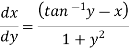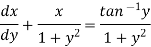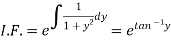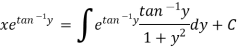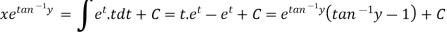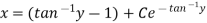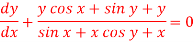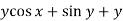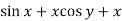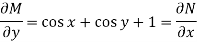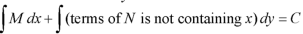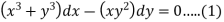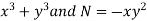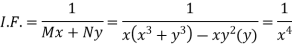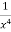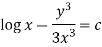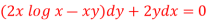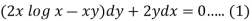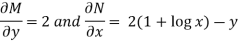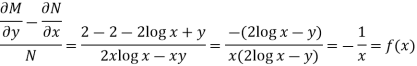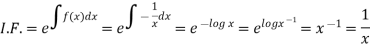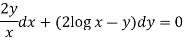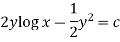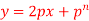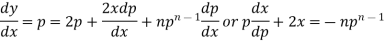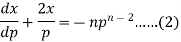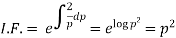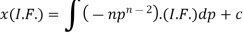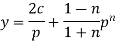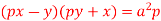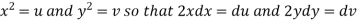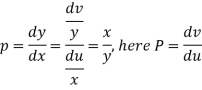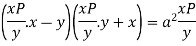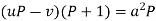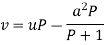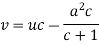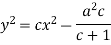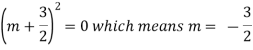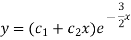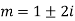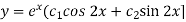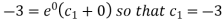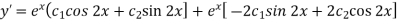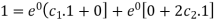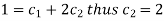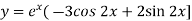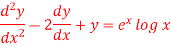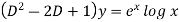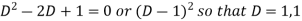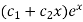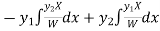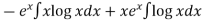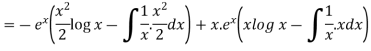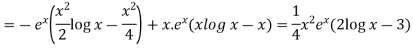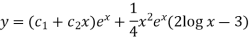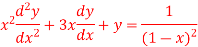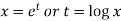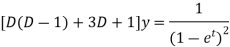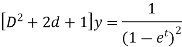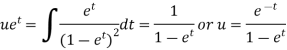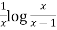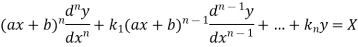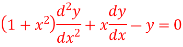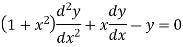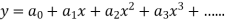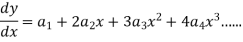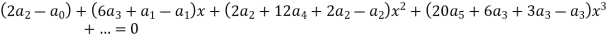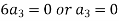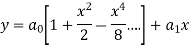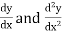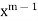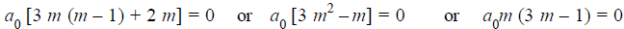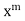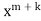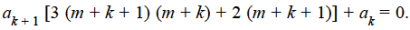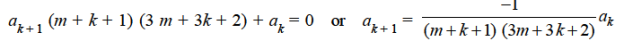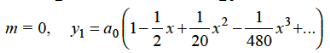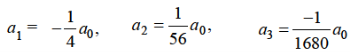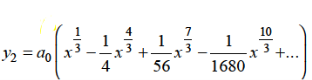We can write the equation as-

We see that it is a Leibnitz’s equation in x-

So that-

Therefore the solution of equation (1) will be-

Or

We can write the equation as-

On dividing by , we get-

Put so that

Equation (1) becomes,

Here,

Therefore the solution is-

Or

Now put

Integrate by parts-

Or
 

Here given-

We can re-write this as-

Which is a linear differential equation-

The solution will be-

Put

We can write the equation as below-

Here M = and N =

So that-

The equation is exact and its solution will be-

Or

We can write the given equation as-

Here,

M =

Multiply equation (1) by we get-

This is an exact differential equation-

Here given,

M = 2y and N = 2x log x - xy

Then-

Here,

Then,

Now multiplying equation (1) by 1/x, we get-

Here we have-

Now differentiate it with respect to x, we get-

Or

This is the Leibnitz’s linear equation in x and p, here

Then the solution of (2) is-

Or

Or

Put this value of x in (1), we get

Put

So that-

Then the given equation becomes-

Or

Or

Which is the Clairaut’s form.

Its solution is-

i.e.

y’’+3y’+2.25y = 0.

We get auxiliary equation as-

Here the roots are repeated.

So that the general solution will be-

y’’-2y’+5y = 0, y(0) = -3, y’(0) = 1.

Here the auxiliary equation will be-

So that-

We get complex conjugate here-

The general solution in this case will be-

Now using y(0) = -3 in general solution, we get-

Now differentiate GS with respect to x-

Using- y’(0) = 1, we get-

Particular solution is-

This can be written as-

C.F.-

Auxiliary equation is-

So that the C.F. will be-

P.I.-

Here

Now

Thus PI = 

            = 

            = 

So that the complete solution is-

On putting so that,

and

The given equation becomes-

Or it can be written as-

So that the auxiliary equation is-

C.F. =

Particular integral-

Where

It’s a Leibnitz’s linear equation having I.F.=

Its solution will be-

P.I. =

       =

So that the complete solution is-

An equation of the form-

Is called Legendre’s linear equation.

Here we have-

Let the solution of the given differential equation be-

Since x = 0 is the ordinary point of the given equation-

Put these values in the given differential equation-

Equating the coefficients of various powers of x to zero, we get-

Therefore the solution is-

Here we have

………… (1)

Since x = 0 is a regular singular point, we assume the solution in the form

So that

Substituting for y, in equation (1), we get-

…..(2)

The coefficient of the lowest degree term in (2) is obtained by putting k

= 0 in first summation only and equating it to zero. Then the indicial equation is

Since

The coefficient of next lowest degree termin (2) is obtained by putting

k = 1 in first summation and k = 0 in the second summation and equating it to zero.

Equating to zero the coefficient of the recurrence relation is given by

Or

Which gives-

Hence for-

Form m = 1/3-

Hence for m = 1/3, the second solution will be-

The complete solution will be-