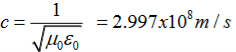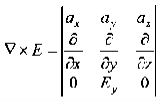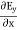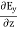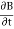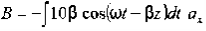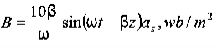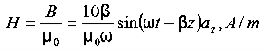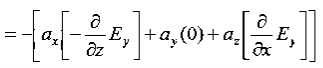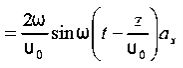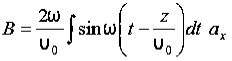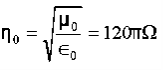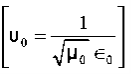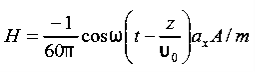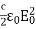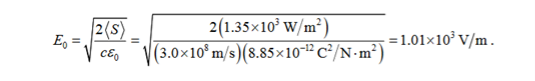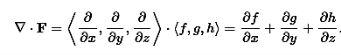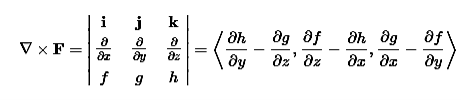|
∇·E = ρ/ε0 (1) ∇×E = −∂B/∂t (2) ∇×H = J + ∂D/∂t (3) ∇·B = 0 (4) |
∇=(∂/∂x, ∂/∂y, ∂/∂z) E is the electric vector B is the magnetic induction ρ is the electric charge density j is the electric current density ε0 is the permittivity of free space c is the speed of light. In addition to Maxwell equations, the following identities are useful: J = σE (5) D = εE (6) B = μH (7) |
D is the electric displacement H is the magnetic vector σ is the specific conductivity ε is the dielectric constant (or permittivity) μ is the magnetic permeability Free space or non-conducting medium. We know that non conducting medium means no current so conductivity is zero i.e. σ=0 So current density J=σE will also become zero as σ=0 Also free space means no charges which leads to ρ=0. These points mentioned below. (a) No condition current i.e σ=0, thus J=0 ( J=σE) (b) No charges (i.e ρ=0) For the case of no charges or currents, that is, j = 0 and ρ = 0, and a homogeneous medium. Using these the Maxwell equation can rewritten as ∇.D=0 or ∇.E=0 as ρ=0 (12) ∇ x E= -dB/dt or ∇ x E= -μ dH/dt because B = μH (13) ∇ x H=d D/dt or ∇ x H = ε dE/dt (J=0) and D = εE (14) ∇.B=0 (15) |
∇ x(∇ x E)=- μ d/dt (∇ x H) Applying standard vector identity, that is [∇ *(∇*E)=∇(∇.E)-∇2E] on left hand side of above equation, we get ∇ (∇ .E)-∇2E= -μ d/dt (∇ x H) (16) Substituting equations (13) and (14) in equations (16) ,we get -∇2E= – με d/dt (dE/dt) Or ∇2E=με d 2 E/dT2 (17) |
∇x(∇xH)=ε d/dt(∇xE) Applying standard vector identity that is [∇*(∇*H)=∇ (∇.H)-∇2H] On left side of above equation , we get ∇(∇.H)-∇2H= ε d/dt(∇xE) (18) Substituting equations (14) and (13) in equation(18) ,we get -∇2H= – μεd/dt(dH/dt) Or ∇2H=με d2H/dt2 (19) Equations (19) is the required wave equation in terms of magnetic field intensity, H and this is the law that H must obey For vacuum μ=μ0 and ε=ε0, equations (17) and (19) will become ∇2 E=μ0ε0 d2E/dt2 (20) And ∇2H= μ0ε0 d2H/dt2 (21) This leads to an expression for the velocity of propagation From equation both equations (20) and (21) have the form of the general wave equation for a wave
(x,t) traveling in the x direction with speed v. Equating the speed with the coefficients, we derive the speed of electric and magnetic waves, which is a constant that we symbolize with “c” It is useful to note that in vacuum c2=1/ε0μ0 Where μ0 is the permeability of free space
Let us rewrite the equation (20) and (21) for one dimension. Or d 2 E/dx2 = μ0ε0 d 2 E/dt2 (22) d2H/dx2 = μ0ε0 d2H/dt2 (23) The simplest solutions to the differential equations (22) and (23) are sinusoidal wave functions: E(x) = Emax cos(kx-t) (24) B(x) = Bmax cos(kx-t) (25) where k = 2π/λ is the wavenumber , ω = 2πƒ is the angular frequency, λ is the wavelength, f is the frequency and ω /k=f=v= c. |
E = 10 sin (t-y) ay, V/m D =0E, 0= 8.854 x 10-12 F/m D = 100sin (t-y) ay, C/m2 Second Maxwell’s equation is x E = -B That is,
or
As Ey= 10 sin (t-z) V/m
Now,x E becomes x E = - = 10 cos (t-z) ax = -
|
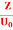 ) ay V/m, Find the magnetic field, HA3)
) ay V/m, Find the magnetic field, HA3)We have B/t =-x E
Thus
Also
|
|
The intensity of the laser beam is I = The amplitude of electric field is therefore
=0.87 V/m The amplitude of magnetic field can be obtained by B0 = E0/ c =2.9 x 10-9 T |
) (a)The time-averaged Poynting vector is related to the amplitude of the electric field by <S> = = The amplitude of electric field is therefore
B0 = E0/ c = The associated magnetic field is one tenth of the earth’s magnetic field. (b) The total time averaged power radiated by the Sun at the distance R is <P> =<S>A =<S> 4πR2 =1.35x103 4 x 3.14 x (1.50x1011)2 = 3.8 x 1026 W The type of wave discussed in the example above is a spherical wave, which originates from a “point-like” source. The intensity at a distance r from the source is which decreases is . I =<S> = <P> /4πR2 Which decreases as 1/r2, On the other hand, the intensity of a plane wave remains constant and there is no spreading in its energy. |
|
∇·E = ρ/ε0 0r ∇·D = ρ |
∇×E = −∂B/∂t (2) |
∇×H = J + ∂D/∂t |
∇·E = ρ/ε0 (1) ∇×E = −∂B/∂t (2) ∇×H = J + ∂D/∂t (3) ∇·B = 0 (4) |
J = σE (5) D = εE (6) B = μH (7) Here, D is the electric displacement H is the magnetic vector σ is the specific conductivity ε is the dielectric constant (or permittivity) μ is the magnetic permeability |
|
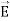 and
and  . Poynting vector is also called as instantaneous energy flux density. Here rate of energy transfer
. Poynting vector is also called as instantaneous energy flux density. Here rate of energy transfer 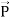 is perpendicular to both
is perpendicular to both 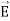 and
and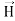 . It represents the rate of energy transfer per unit area.UNITIts unit is W/m2. Q10) What do you mean by gradient? Give its physical significance.A10) GRADIENT OF SCALAR FIELD The gradient is a fancy word for derivative, or the rate of change of a function. It’s a vector (a direction to move) that
. It represents the rate of energy transfer per unit area.UNITIts unit is W/m2. Q10) What do you mean by gradient? Give its physical significance.A10) GRADIENT OF SCALAR FIELD The gradient is a fancy word for derivative, or the rate of change of a function. It’s a vector (a direction to move) that
|
|
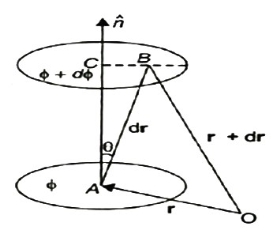
dn = dr cos θ = | n | dr | cos θ =n .dr Dϕ = ∂ϕ/ dn =∂ϕ/dn n .dr…… (1) Since the continuous scalar function defining the level surfaces (Gaussian surfaces) has a value θ at point A (x, y, z) and (θ + dθ) at point (x + dx, y + dy, z + dz), we have dϕ = ∂ ϕ/dx dx +dϕ/∂y + ∂ϕ/∂x dz = (I ∂ϕ/∂x +j ∂ϕ/vy +k ∂ϕ/∂z) .(idx +jdy +kdz) = ∆ ϕ. dr … … (2) From equations (1) and (2), equating the values of d θ, We obtain ∆θ .dr =∆ ϕ= ∂ϕ/ ∂n n .dr As dr is an arbitrary vector, we have ∆ϕ =∂ϕ/∂ n Grad ϕ = ∂ ϕ/∂n n |
|
|
∇f=⟨∂f/∂x, ∂f/∂y, ∂f/∂z⟩ Where ∇ =⟨∂/∂x, ∂/∂y, ∂/∂z⟩ The divergence can be defined in terms of this same odd vector ∇ by using the dot product. The divergence of a vector field F=⟨f,g,h⟩ is
|
|
|
|
|
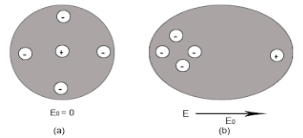
Volume of the sphere of radius x = (4/3)πx3 and Volume of the sphere of radius R = (4/3)πR3 Now total negative charge of the electron cloud is -Ze …..(2) Hence, the quantity of negative charge enclosed by the sphere of radius x is, [-Ze/(4/3)πR3] * (4/3)πx3 = -Ze (x3/ R3) ……..(3) According to coulomb’s law = q1q2 /4 πR2 Charge on nucleus q2= Ze So coulomb’s force = {-Ze (x3/ R3) * Ze}/4πƐox2 = Z2e2x/4πƐo R3 ……(4) Note- magnitude is taken into account. Neglect negative sign. i.e. At equilibrium Electrostatic force = Coulomb force . EZe = Z2e2x/4πƐoR3 ……..(5) Upon simplify x = {4πƐoR3/Ze} E Now dipole moment = either charge * separation between charges i.e. x = Ze *{4πƐoR3/Ze} E = 4πƐoR3E Polarization is number of dipole moment per unit volume. Let us suppose N is the number of dipoles per unit volume so Pe=4πƐoR3EN |
|
|
|
F1=qE ……(1) Where q is the net charge on ion. F2 restoring force due to binding force between ions F2=kd …..(2) Where k is spring constant. Here we are considering bond as spring. k may also expressed in terms of other constant which is related to the shape of interatomic potential as young’s modulus or modulus of rigidity as k=Ydo …..(3) At Equilibrium F1 = F2 at equilibrium distance d qE = kd qE = Ydod using (3) d = Now dipole moment p= qd = q2E/Ydo …..(4) and polarization Pi = Nq2E / Ydo ……(5) This is called ionic polarization. This can also be expressed as Pi =NαiE Where αi is constant of proportionality known as ionic polarizability constant. This polarization is independent of temperature. |
|
U=−p0⋅E=−p0Ecosθ According to statistical mechanics, the number of dipoles or molecules making an angle with the electric field is proportional to e−U/kT Letting n(θ) be the number of molecules per unit solid angle at θ, we have n(θ)=n0e+p0Ecosθ/kT For normal temperatures and fields, the exponent is small, so we can approximate by expanding the exponential: n(θ)= n0 (1+p0EcosθkT) To find n0 , we integrate over all angles and the result is equal to N. Where N is the total number of molecules per unit volume. The average value of cosθ over all angles is zero, so the integral is just n0 times the total solid angle 4π. We get n0=N4π or N= n0 /4π |
present so polarization Pd is given Pd =∑unitvolumep0cosθi Evaluate Total Polarization over solid angle 2πsinθdθ. We have to integrate it Pd = 0∫π n(θ)p0cosθ2πsinθdθ Substitute the value of n(θ) Pd = −N/2 −1∫1 {1+(p0E/kT)cosθ)p0cosθd(cosθ) By integrating we get, Pd =Np02E/ 3kT |
|