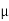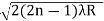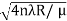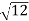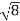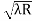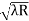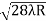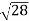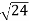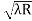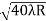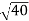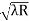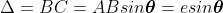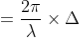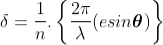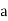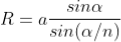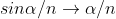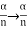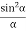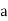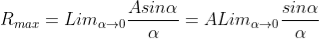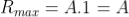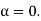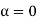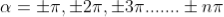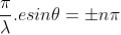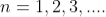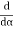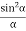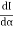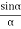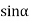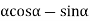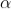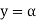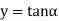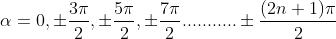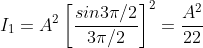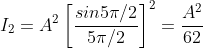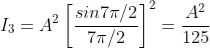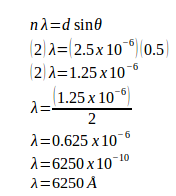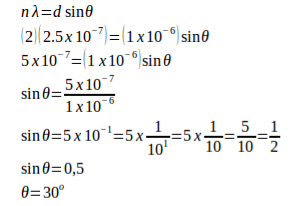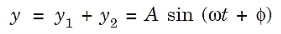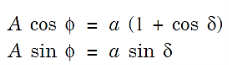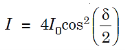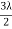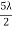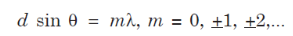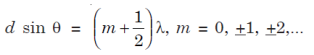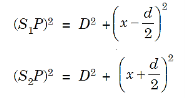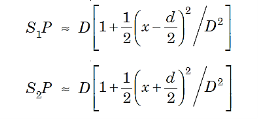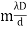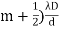Given: number of lines per cm =4000 Grating element e+b = 1/4000 cm = 2.5 x 10-6m λ=500 nm Order n =1 (e+b) sinθ =nλ sinθ = nλ / (e+b) sinθ = 1 x 500 x 10-9 / 2.5 x 10-6 sinθ =0.2 θ =sin-1 0.2 θ = 11.5o |
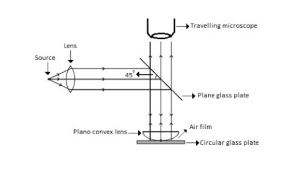
The given data are Diameter of Newton’s 15th ring (D15) = 0.59 cm = 0.59×10–2 m Diameter of Newton’s 5th ring (D5) = 0.336 cm = 0.336 × 10–2 m Radius of curvature of lens (R) = 100 cm = 1 m Wave length of light (λ) = ? Here m is difference between rings = 15-5=10 λ = D2n+m - D2n / 4mR λ = (0.59×10–2 )2- (0.336 × 10–2)2 / 4 x 10 x 1 λ = 0.3481 x10-4 – 0.112896 x10-4 / 40 λ =0.00588 x 10-4 m λ =5880 x 10-10 m λ =5880Å |
|
|
(OL)2 =(O’M)2-(ML)2 ……….(1) R2=(R-t)2 +rn2 R2=R2 +t2-2Rt +rn2 Radius is large as compared to the thickness so t2 is neglected as t2<< R2 R2=R2 +-2Rt +rn2 2Rt =rn2 Thickness of the film t =rn2 /2R ……….(2) |
∆ = 2μtcos(r+θ) +λ/2 ……….(3) If the light is incident normally on the lens, r = 0 and near to point of contact θ is small; Therefore near point of contact, (r+θ) approaches to 0 and cos(r+θ)=cos0=1 Therefore ∆ = 2μt+λ/2 ……….(4)
Also At point of contact t = 0 therefore the effective path difference ∆ = λ/2 Which is odd multiple of λ/2 Therefore the Central fringe is dark. Bright Fringe : Condition of Maxima For the condition of maxima the effective path difference ∆ = ±nλ Using equation (4) ∆ = 2μt+λ/2 we have 2μt+λ/2= ±nλ 2μt = ± (2n-1)λ /2 ……….(5) |
we know by equation (2) t =rn2 /2R substitute in equation (5) we have 2μ (rn2 /2R) = ± (2n-1)λ /2 rn2 = ± (2n-1)λR /2μ We know diameter D=2r and for nth fringe Dn=2rn so we have Dn2=± 2(2n-1)λR /μ Dn= The medium enclosed between the lens and glass plate is if air therefore, D= The diameter of bright ring is proportional to square root of odd natural numbers Dark Fringe : Condition for Minima For the condition of minima, The effective path difference ∆ =± (2n+1)λ /2 2μt+λ/2 =± (2n+1)λ /2 2μt= ±nλ ……….(7) it is clear that for particular dark or bright fringe t should be constant. Every fringe is the locus of points having equal thickness. Hence the fringes are circular in shape. Diameter of Dark Rings we know by equation (2) t =rn2 /2R substitute in equation (7) we have 2μ (rn2 /2R ) = nλ rn2 = nλR/ μ We know diameter D=2r and for nth fringe Dn=2rn so we have Dn2= 4nλR/ μ Dn= The medium enclosed between the lens and glass plate is if air therefore, Dn= The diameter of dark ring is proportional to square root of natural numbers |
The given data are Wave length of light (λ) = 5900 Å= 5900 × 10–10 m Diameter of 10th Newton’s dark ring (D10) = 0.5 cm = 0.5 × 10–2 m Radius of curvature of lens (R) = ? Formula is D2n = 4nλR R= D2n /4nλ R= (0.5 × 10–2)2 /4x 10 x 5900 × 10–10 R= 0.25 x10-4 /236x10-7 R=1.059m |
For example the diameter of dark ring is given by Dn= D3 - D2 = D7 – D6 = D10– D9 = |
|
|
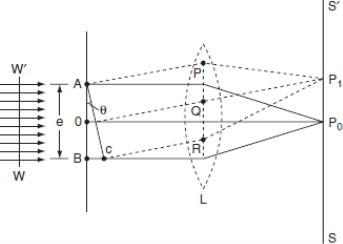
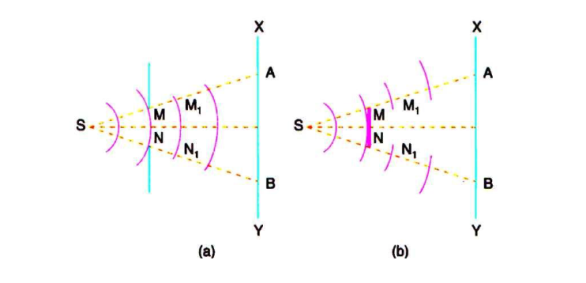
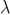 ' is incident on the slit. Let the diffracted light be focused by means of a convex lens on a screen. According to Huygen Fresnel, every point of the wavefront in the plane of the slit is a source of secondary wavelets. The secondary wavelets traveling normally to the slit i.e., along OP0 are brought to focus at P0 by the lens. Thus P0 is a bright central image. The secondary wavelets traveling at an angle '
' is incident on the slit. Let the diffracted light be focused by means of a convex lens on a screen. According to Huygen Fresnel, every point of the wavefront in the plane of the slit is a source of secondary wavelets. The secondary wavelets traveling normally to the slit i.e., along OP0 are brought to focus at P0 by the lens. Thus P0 is a bright central image. The secondary wavelets traveling at an angle '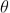 ' are focused at a point P1 on the screen.The intensity at the point P1 is either minimum or maximum and depends upon the path difference between the secondary waves originating from the corresponding points of the wavefront.
' are focused at a point P1 on the screen.The intensity at the point P1 is either minimum or maximum and depends upon the path difference between the secondary waves originating from the corresponding points of the wavefront.
|
So, the phase difference,
Let us consider that the width of the slit is divided into ‘n’ equal parts and the amplitude of the wave from each part is ‘a’. So, the phase difference between two consecutive points
|
|
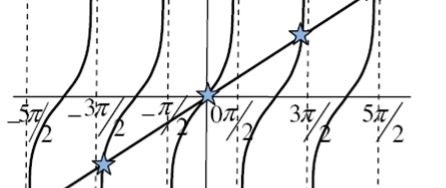
The resultant amplitude of n number of waves having same amplitude 'a' and having common phase difference of '
Substituting the value of R = a Substituting As R = n and na = A Therefore R =A Therefore, the Intensity is given by I =R2 = A2 Case (i): Principal Maximum: Eqn (4) takes maximum value for
sinθ = 0 or θ=0 The condition The condition θ=0 means that this maximum is formed by the secondary wavelets which travel normally to the slit along OP0 and focus at P0. This maximum is known as “Principal maximum”. Intensity of Principal maxima
Therefore Imax = R2max = A2 Case (ii): Minimum Intensity positions: Equation (3) takes minimum values for sin
|
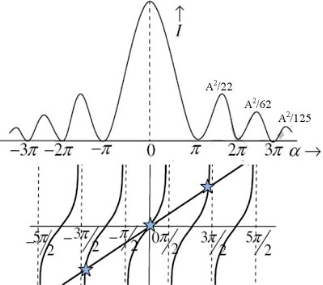
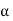 = 0, there are weak secondary maxima between minima positions. The positions of these weak secondary maxima can be obtained with the rule of finding maxima and minima of a given function in calculus. So, differentiating equation (5) and equating to zero, we have
= 0, there are weak secondary maxima between minima positions. The positions of these weak secondary maxima can be obtained with the rule of finding maxima and minima of a given function in calculus. So, differentiating equation (5) and equating to zero, we have
A2
Because
The values of ' The points of intersection of the two curves gives the values of The points of intersections are |
|
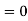 , gives principal maximum, substituting the values of
, gives principal maximum, substituting the values of 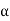 in equation (5), we get
in equation (5), we getand so on.
|
 ' is as shown in the adjacent figure
' is as shown in the adjacent figure
|
|
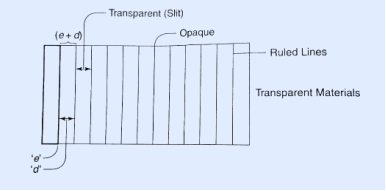
Then (e + d) is known as grating element. If N is the number of lines per inch on the grating then (𝑒+𝑑)=1𝑖𝑐ℎ=2.54𝑐𝑚 (𝑒+𝑑)=2.54𝑐𝑚/𝑁 |
The distance between slits (d) = 1 / (4000 slits / cm) = 0.00025 cm = 2.5 x 10-4 cm = 2.5 x 10-6 meters Order (n) = 2 Sin 30o = 0.5 1 Å = 10-10 m Wavelength of the light (λ) =?
|
Given The distance between slits (d) = 1 / (10,000 slits / cm) = 0.0001 cm = 1 x 10-4 cm = 1 x 10-6 m Order (n) = 2 Wavelength (λ) = 2.5 x 10-7 m Angle (θ)
|
Wavelength (λ) = 500.10-9 m = 5.10-7 m θ = 30o n = 2 Distance between slits: d sin θ = n λ d (sin 30o) = (2)(5.10-7) d (0.5) = 10.10-7 d = (10.10-7) / 0.5 d = 20.10-7 d = 2.10-6 m Number of slits per centimetre: x = 1 / d x = 1 / 2.10-6 m x = 0.5.106 / 1 m x = 0.5.106 / 102 cm x = 0.5.104 cm x = 5.103 /cm x = 5000 /cm |
Wavelength (λ) = 500.10-9 m = 5.10-7 m θ = 30o n = 4 Distance between slits: d sin θ = n λ d (sin 30o) = (4)(5.10-7) d (0.5) = 20.10-7 d = (20.10-7) / 0.5 d = 40.10-7 d = 4.10-6 m Number of slits per centimetre: x = 1 / 4.10-6 m x = 0.25.106 / m x = 0.25.106 / 102 cm x = 0.25.104 / cm x = 25.102 per cm x = 2500 per cm |
|
y1 = f1(x–vt), y2 = f2(x–vt) ………. yn = fn (x–vt) then the wave function describing the disturbance in the medium can be described as y = f1(x – vt)+ f2(x – vt)+ …+ fn(x – vt) or, y= Let us consider a wave travelling along a stretched string given by, y1(x,t) = A sin (kx – ωt) and another wave, shifted from the first by a phase φ, given as y2(x, t) = A sin (kx – ωt + ϕ) From the equations we can see that both the waves have the same angular frequency, same angular wave number k, hence the same wavelength and the same amplitude A. Now, applying the superposition principle, the resultant wave is the algebraic sum of the two constituent waves and has displacement y(x, t) = A sin (kx – ωt) + A sin (kx – ωt + ϕ) As, sin A + sin B = 2sin (A+B)/2 .cos (A−B)/2 The above equation can be written as, y(x, t) = [2A cos ϕ /2 ] sin (kx − ωt + ϕ /2) |
|
|
|
|
|
|
y= a sin ( |
|
|
|
|
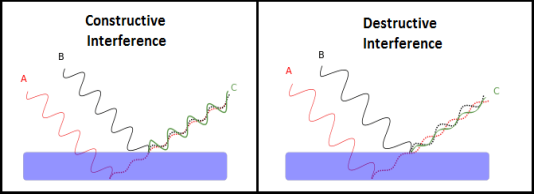
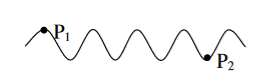
where Δ = S2P – S1P is the path difference. Let us consider y1 is the displacement due to the waves coming from S1 and y2 is displacements due to the waves coming from S2, Thus we have
where a is the amplitude of both the waves. According to the principle of superposition, the resultant displacement y is given by
where
and A is the amplitude of the resultant displacement. Thus,
The intensity I of the light at P is proportional to the square of the resultant amplitude.
Thus, we can write the equation (5) as
where I0 is the intensity on the screen associated with light from one of the two slits, the other slit being temporarily covered. For maximum intensity, δ = 0, 2π, 4π,... or, path difference Δ = 0, λ, 2λ... ; and for minimum intensity δ = π, 3π, 5π,... or, Δ = The point P0 on the screen is equidistant from S1 and S2. At P0, Δ = 0 and δ = 0. We have maximum intensity at P0. From S1 we drop a perpendicular S1Q on S2P and suppose ∠ S2S1Q = θ, then Δ = d sin θ and δ =2π λ d sin θ, where d = S1S2 = separation between the coherent sources. Thus, the conditions for maxima and minima are Maxima
Minima
Suppose the point P is at a distance x from P0 and D is the distance of the screen from the coherent sources. Then
D is the distance between slits and screen which is usually very large compared to d or x. Then, we can write
The path difference Δ becomes
where ∠POP0 = θ and The conditions for bright and dark fringes are Bright fringes x = Dark fringes x =( At P0, m = 0, i.e., zeroth order bright fringe is formed at P0. The distance between any two consecutive bright or dark fringes is known as fringe width and it is given by β =(
|