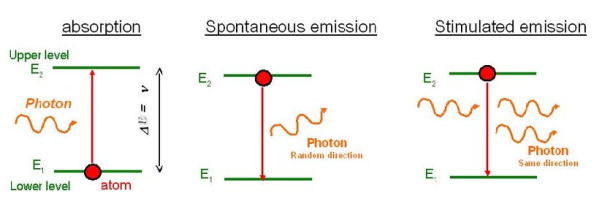
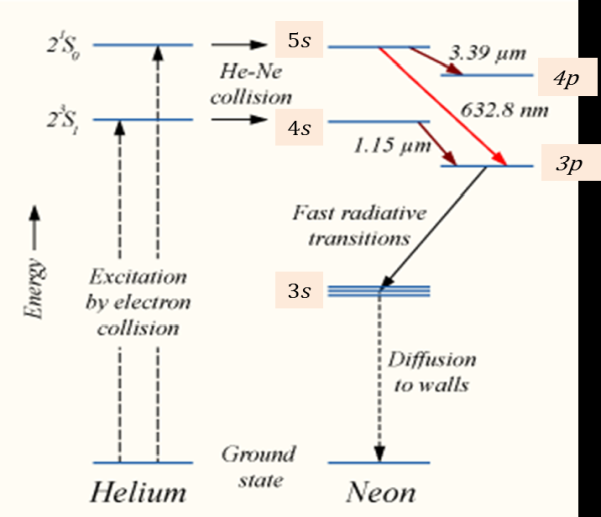
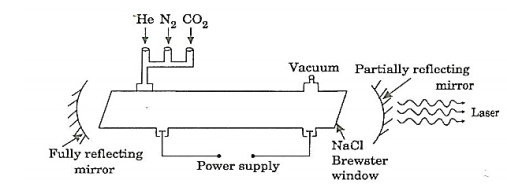
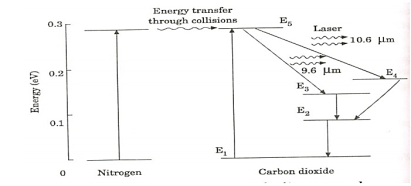
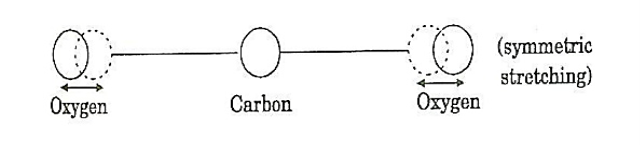
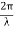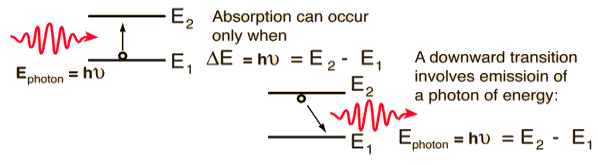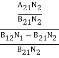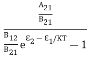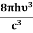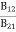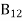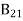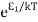Spontaneous emission | Stimulated emission |
1.The spontaneous emission was postulated by Bohr | 1.The stimulated emission was postulated by Einstein |
2. Additional photons are not required in spontaneous emission | 2. Additional photons are required in stimulated emission |
3.One photon is emitted in spontaneous emission | 3.Two photons are emitted in stimulated emission |
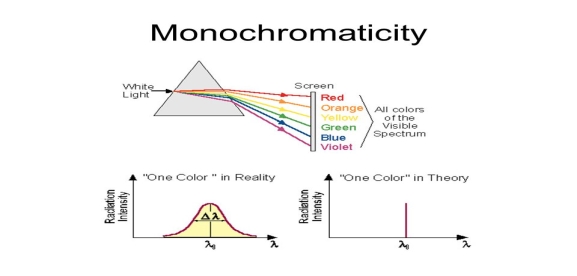
4.The emitted radiation is poly-monochromatic | 4.The emitted radiation is monochromatic |
5. The emitted radiation is Incoherent | 5. The emitted radiation is Coherent |
6. The emitted radiation is less intense | 6. The emitted radiation is high intense |
7.The emitted radiation has less directionality | 7.The emitted radiation has high directionality |
8. Example: light from sodium or mercury lamp | 8. Example: light from the laser source.
|
Stimulated absorption rate ∝ Number of atoms in the ground state ∝ The density of photons Spontaneous emission |
|
Stimulated emission rate ∝ number of atoms in the excited state ∝ Density of photons |
|
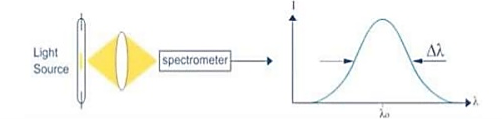
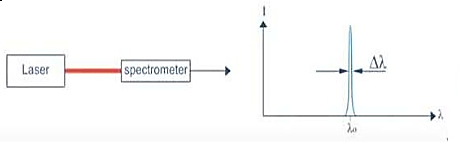
Figure 6: Intensity- wavelength graph for light and laser
|
|
|
y= a sin ( |
|
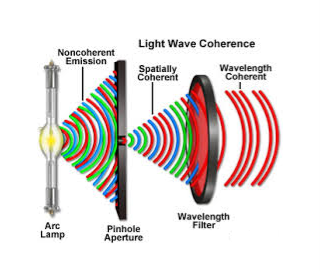
 Where r1 and r2 are the radii of laser beam spots at distances of D1 and D2 respectively from the laser source. 4. Highly Intense or Brightness We know that the intensity of a wave is the energy per unit time flowing through a unit's normal area. Laser light is highly intense than conventional light. A one mill watt He-Ne laser is highly intense than the sun intensity. This is because of the coherence and directionality of the laser. Suppose when two photons each of amplitude a are in phase with other, then young’s principle of superposition, the resultant amplitude of two photons is 2a and the intensity is 4a2. Since in laser many numbers of photons are in phase with each other, the amplitude of the resulting wave becomes na and hence the intensity of the laser is proportional to n2a2. So 1mW He-Ne laser is highly intense than the sun.In an ordinary light source, the light spreads out uniformly in all directions. If you look at a 100 Watt lamp filament from a distance of 30 cm, the power entering your eye is less than 1/1000 of a watt. If you look at laser beam X(caution: don’t do it at home, direct laser light can damage your eyes)X, then all the power in the laser would enter your eye. Thus, even a 1 Watt laser would appear many thousand times more intense than a 100 Watt ordinary lamp. 5. Laser Speckles The term speckle refers to a random granular pattern that can be observed when a highly coherent light beam is diffusely reflected at a surface with a complicated structure. This phenomenon results from the interference of different reflected portions of the incident beam with random relative optical phases.
Where r1 and r2 are the radii of laser beam spots at distances of D1 and D2 respectively from the laser source. 4. Highly Intense or Brightness We know that the intensity of a wave is the energy per unit time flowing through a unit's normal area. Laser light is highly intense than conventional light. A one mill watt He-Ne laser is highly intense than the sun intensity. This is because of the coherence and directionality of the laser. Suppose when two photons each of amplitude a are in phase with other, then young’s principle of superposition, the resultant amplitude of two photons is 2a and the intensity is 4a2. Since in laser many numbers of photons are in phase with each other, the amplitude of the resulting wave becomes na and hence the intensity of the laser is proportional to n2a2. So 1mW He-Ne laser is highly intense than the sun.In an ordinary light source, the light spreads out uniformly in all directions. If you look at a 100 Watt lamp filament from a distance of 30 cm, the power entering your eye is less than 1/1000 of a watt. If you look at laser beam X(caution: don’t do it at home, direct laser light can damage your eyes)X, then all the power in the laser would enter your eye. Thus, even a 1 Watt laser would appear many thousand times more intense than a 100 Watt ordinary lamp. 5. Laser Speckles The term speckle refers to a random granular pattern that can be observed when a highly coherent light beam is diffusely reflected at a surface with a complicated structure. This phenomenon results from the interference of different reflected portions of the incident beam with random relative optical phases.
|
|
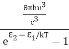
Stimulated absorption rate ∝ N1 i.e. Number of atoms in the ground state ∝ ρ(υ) i.e. Density of photons spontaneous emission Stimulated absorption rate = B12N1ρ(υ) ………(1) Where B12 is the Einstein coefficient of stimulated absorption. Downward transition The spontaneous emission rate depends upon the number of atoms present in the excited state. Spontaneous emission rate ∝ N2 i.e. number of atoms in the excited state Spontaneous emission rate = A21N2 ………(2) Where A21 is the Einstein coefficient of spontaneous emission. Stimulated emission rate depends upon the number of atoms available in the excited state as well as the energy density of photons. Stimulated emission rate ∝ N2 i.e. number of atoms in the excited state ∝ ρ(υ) i.e. Density of photons Stimulated emission rate = B21N2ρ(υ) ………(3) If the system is in equilibrium the upward transitions must be equal to downward transitions. upward transitions = downward transitions B12N1ρ(υ) = A21N2 + B21N2ρ(υ) ………(4) B12N1ρ(υ) - B21N2ρ(υ) = A21N2 (B12N1- B21N2) ρ(υ) = A21N2 ρ(υ) = Divide with B21N2 in numerator and denominator in the right side of the above equation, ρ(υ) = ρ(υ) = We know from Maxwell Boltzmann distribution law
And also from Planck’s law, the radiation density ρ(υ) = Comparing the two equations (7) and (9)
The above relations are referred to as Einstein relations. From the above equation for non-degenerate energy levels, the stimulated emission rate is equal to the stimulated absorption rate at the equilibrium condition.
|
a) B12 > B21
b) B12 < B21
c) B12 = B21
d) No specific relationA5)C is the correct answer.
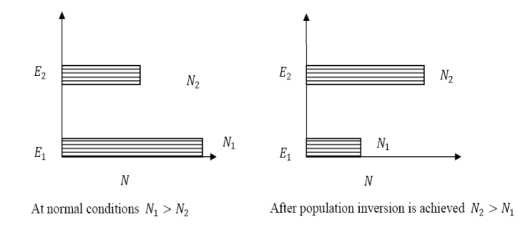
B21 is the coefficient for the stimulated emission while B12 is the coefficient for stimulated absorption. Both the processes are mutually reverse processes and their probabilities are equal. Therefore, B12 = B21. Q6) How laser light get amplify by population inversion?A6)Population inversionDefinitionThe number of atoms present in the excited state or higher energy state is greater than the number of atoms present in the ground state or lower energy state is called population inversion.Population inversion as the name suggests that this is an inverted phenomenon. In general, the lower energy level is more populated which means it has more number atoms in the lower energy level as compared to a higher energy level. But by pumping we will obtain a state when the number of atoms present in the higher energy state is greater than the number of atoms present in the lower energy state.Let us consider a two-level energy system of energies E1 and E2 as shown in the figure. Let N1 and N2 be the populations that mean several atoms per unit volume of energy levels E1 and E2 respectively.According to Boltzmann’s distribution the population of an energy level E, at temperature T is given by
Ni=N0 |
N1=N0 N2=N0 |
|
|
|
|
|
|
|
When an electric discharge occurs in the gas, the electrons collide with nitrogen molecules and they are raised to excited states. This process is represented by the equation N2 + e* = N2* + e N2 = Nitrogen molecule in ground state e* = electron with kinetic energy N2* = nitrogen molecule in excited state e= same electron with lesser energy Now N2 molecules in the excited state collide with CO2 atoms in ground state and excite to higher electronic, vibrational and rotational levels. This process is represented by the equation N2* + CO2 = CO2* + N2 N2* = Nitrogen molecule in excited state. CO2 = Carbon dioxide atoms in ground state CO2* = Carbon dioxide atoms in excited state N2 = Nitrogen molecule in ground state. Since the excited level of nitrogen is very close to the E5 level of CO2 atom, population in E5 level increases. |
|
|
|