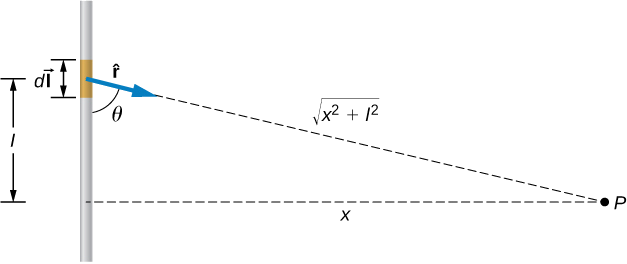
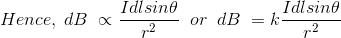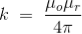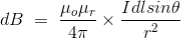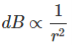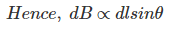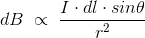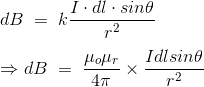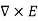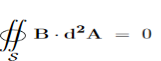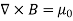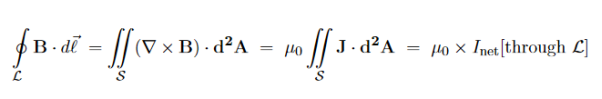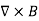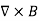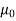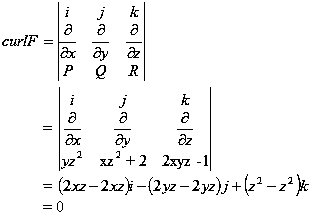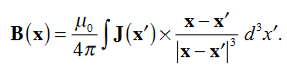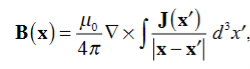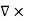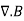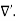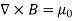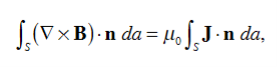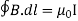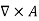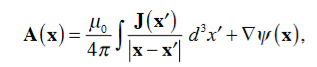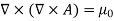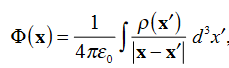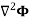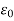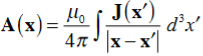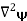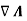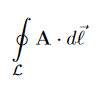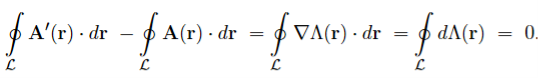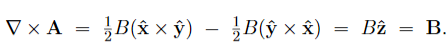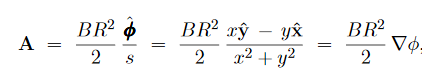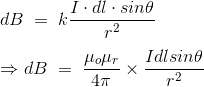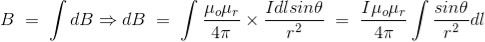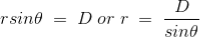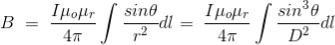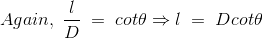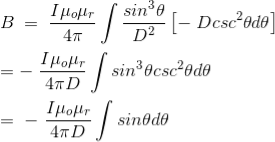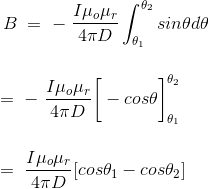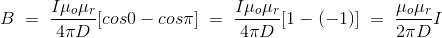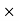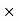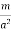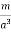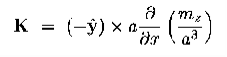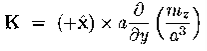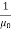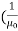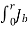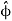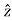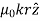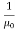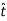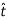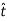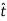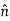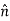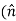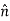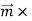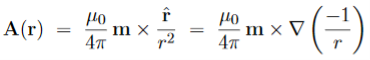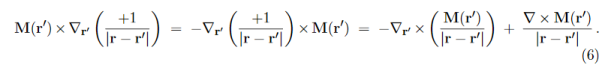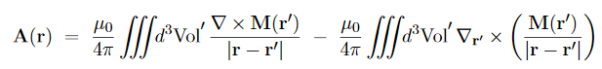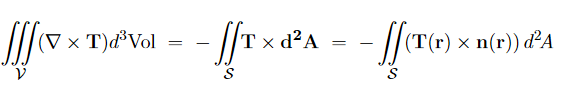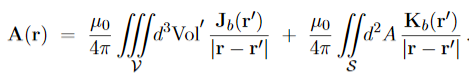The Biot Savart Law is an equation describing the magnetic field generated by a constant electric current. It relates the magnetic field to the magnitude, direction, length, and proximity of the electric current. Biot–Savart law is consistent with both Ampere’s circuital law and Gauss’s theorem. The Biot-Savart law is fundamental to magnetostatics, playing a role similar to that of Coulomb’s law in electrostatics.

The Biot-Savart law can be stated as:

    ……….(1)

Where, k is a constant, depending upon the magnetic properties of the medium and system of the units employed.

In the SI system of unit,

          ……….(2)

Therefore, the final Biot-Savart law derivation is,

        ……….(3)

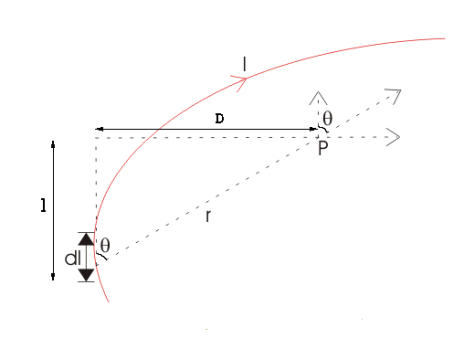
DERIVATION

Let us consider a long wire carrying a current I and also consider a point p in the space. The wire is presented in the picture below, by red colour.

Let us also consider an infinitely small length of the wire dl at a distance r from the point P as shown. Here, r is a distance-vector which makes an angle θ with the direction of current in the infinitesimal portion of the wire.

If you try to visualize the condition, you can easily understand the magnetic field density at point P due to that infinitesimal length dl of the wire is directly proportional to current carried by this portion of the wire.

As the current through that infinitesimal length of wire is the same as the current carried by the whole wire itself, we can write,

         ……….(4)

The magnetic field density at that point P due to that infinitesimal length dl of wire is inversely proportional to the square of the straight distance from point P to the center of dl. Mathematically we can write this as,

         ……….(5)

Figure 1: Biot-Savart law

As θ be the angle between distance vector r and direction of current through this infinitesimal portion of the wire, the component of dl directly facing perpendicular to the point P is dlsinθ,

        ……….(6)

Now, combining these three statements, we can write,

        ……….(7)

This is the basic form of Biot Savart’ s Law

Now, putting the value of constant k (which we have already introduced at the beginning of this article) in the above expression, we get

      ……….(8)

Here, μ0 used in the expression of constant k is absolute permeability of air or vacuum and its value is 4π10-7 Wb/ A-m in the SI system of units. μr of the expression of constant k is the relative permeability of the medium.

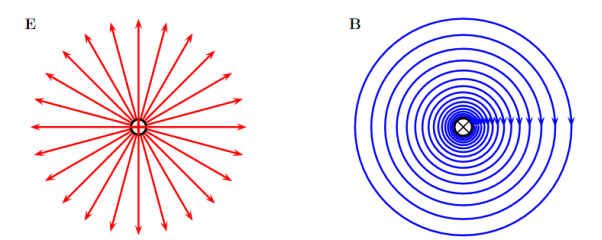
The static electric field E(x; y; z) such as the field of static charges obeys equations

∇. E =ρ         ………..(3.2a)

= 0         ………..(3.2b)

The static magnetic field B(x; y; z) such as the field of steady currents obeys different equations

=0          ………..(3.2c)

J         ………..(3.2d)

Figure 2: Electric and Magnetic Fields

Due to this difference, the magnetic field of long straight wire looks quite different from the electric field of a point charge or a linear charge.

Later in these notes we will derive equations (3.2c) and (3.2d) from the Biot Savart Law.

Let us explore some of their consequences. The zero-divergence equation (3.2c) is valid for any magnetic field, even if it is time-dependent rather than static. Physically, it means that there are no magnetic charges, otherwise we would have ∇.B mag instead of ∇ B= 0.

Consequently, the magnetic field lines never begin or end anywhere in space; instead they form closed loops or run from in infinity to in infinity.

The integral form of eq. (3.2c) follows by the Gauss theorem: the magnetic flux through any closed surface is zero

Consequently, any open surfaces S1,S2,……..spanning the same loop L have the same magnetic flux through them, for example

Figure 3: Open  Surface

We shall this identity very useful for stating the Faraday's Law of magnetic induction.

Now consider the curl equation

J 

which is the differential form of the Ampere's Law. The integral form of the Ampere's Law obtains by the Stokes' theorem: For any closed loop L and any surface S spanning that loop,

………..(3.2e)

Where Inet [through L] is the net electric current flowing through the loop L. The integral form (3.2e) of the Ampere's Law is particularly convenient when the current flows through a wire or several wires; in this case all we need is to check which wire goes through the loop L and which does not, then add up the currents in the wires that do go through L and mind their directions. But it is also convenient for the volume currents flowing through thick conductors or for current sheets flowing on surfaces.

 As we know that the Ampere's Law applies only to the magnetic fields of steady currents. Otherwise, we need to use the more general Maxwell {Ampere Law, with an extra term for the time-dependent electric field.

For simplicity we say that the original Ampere's Law is simply mathematically inconsistent unless the electric current has zero divergence,∇J= 0.Indeed, the left hand side of the curl equation J always have zero divergence.

∇. () = 0

So we cannot have () = J unless the RHS has zero divergence as well,

∇.J= 0. As to the integral form (3.2e) of the Ampere's Law, we need a divergence-less current density J to make sure that the net current through the loop L is the same for any surface S spanning the loop; otherwise we simply cannot de ne the net current through L

it is possible for F(x,y) = x2y, y-xy2 to be a magnetic field, if its divergence would be zero.

If F were magnetic, then its divergence would be zero. The divergence of F is

(x2y)+(y-xy2) = 2xy +1 -2xy =1

and therefore F cannot model a magnetic field

The divergence of vector field F(x,y) = x2y, y-xy2 is one, so it cannot model a magnetic field.

Therefore, the given vector field F is conservative.

In general, when dealing with a current density J(x’) instead of a current I so (equation 1 of article 3.1) for the magnetic induction B(x) takes the form

     ……….(1)

Equation (1) can be expressed differently, since

    ……….(2)

but since

    ……….(3)

We get

     ……….(4)

If we set =1/ and a=J(x’), with J(x’)=0, since the current density is independent of x. It follows from equation (3) that the magnetic induction is divergence-less

=0          ……….(5)

Equation (5) is a mathematical statement on the inexistence of magnetic monopoles.

Taking the curl of the B field,

Using this identity we get

……….(5)

Solving this we get

………..(6)

This equation can be further simplified by using the divergence theorem

Since J(x’)=0  and the surface of integration extends over all space where the integrand vanishes. We therefore find that

J         ………..(7)

If we evaluate the integral on both sides of equation (7) over an open surface S of contour C (see Figure 2), we find

Figure : A magnetic induction is induced around a circuit C by a current density J through the open surface S bounded by C.

and using Stokes’ theorem

     ………..(8)

c         ………..(9) 

where I is the current passing through the surface. Equations (8) and (9) are mathematical representations of Ampère’s Law.

Since we know from equation (3.2c) that the divergence of the magnetic induction is zero, it follows that the B field can be expressed as the curl of another vector field. Introducing the potential vector A(x), we can write

B(x) = (x)         ………..(1) 

Referring to equation (4) of article 3.2, we find that the most general equation for A is

    ………..(2) 

Where  is some arbitrary scalar function. Inserting equation (2)  into equation (3.2d)J             

We get

J        ………..(3) 

= J        ………..(4) 

But because of the freedom brought by the presence of in the equation defining the potential vector (i.e., equation (2)), we can choose to suit our needs. Using the so-called Coulomb gauge, which sets we write

= J         ………..(5) 

Just as

      ………..(6) 

is the solution to the Poisson equation ( = /ρ), the following is the solution to equation

      ………..(7)

Equation (7) is valid in general, as we can set =cste due to the fact that =0

reduces to =0 from equation (2). This is because

    ………..(8)

Since  J(x’)=0. Equation (8) .

The magnetic field B(r) determines the vector potential A(r) only up to a gradient of an arbitrary scalar field (x; y; z). Indeed, the vector potentials A (x; y; z) and

A’(x,y,z) = A(x,y,z) + (x; y; z)      ………..(9)

have the same curl everywhere, so they correspond to the same magnetic field,

B’(x,y,z) = A’(x,y,z) + (x; y; z) = B(x,y,z) +0  ………..(10)

The relations (9) between different vector potentials for the same magnetic field are called the gauge transforms.

Despite ambiguity of the vector potential itself, some of its properties are gauge invariant i.e., the same for all potentials related by gauge transforms. For example, for any closed loop L, the integral.

        ………..(11)

is gauge invariant; indeed,

………..(12)

Physically, the integral (11) in the magnetic flux through the loop L. Indeed, take any surface S spanning the loop L; by the Stokes' theorem,

………..(13)

We may use eq. (13) to easily find the vector potential for a magnetic field which has some symmetries. For example, consider the uniform magnetic field B=B inside a long solenoid. By the rotational and translational symmetries of the solenoid, we expect.

A(s, ϕ, z) = A(s)        ………..(14)

While the magnitude A(s) follows from eq. (13): Take a circle of radius s < R solenoid, then

     ………..(15)

While the magnetic flux through that circle is

      ………..(16)

Hence

     ………..(17)

In Cartesian coordinates, the vector potential becomes

     ………..(18)

Which makes it easy to verify

 ………..(19)

Eq. (18) gives the vector potential inside the long solenoid. Outside the solenoid, the magnetic field is negligible, but the flux through a circle of radius s > R solenoid is non-zero due to the flux inside the solenoid. Thus,

      ………..(20)

and hence

 ………..(21)

In vector notations

  ………..(22)

which agrees with the zero magnetic field outside the solenoid,

   ………..(23)

Figure 1: Biot-Savart law

Biot-Savrat law is given by

      ……….(8)

Here, μ0 used in the expression of constant k is absolute permeability of air or vacuum and its value is 4π10-7 Wb/ A-m in the SI system of units. μr of the expression of constant k is the relative permeability of the medium.

Now, flux density (B) at the point P due to the total length of the current-carrying conductor or wire can be represented as,

 ……….(9)

If D is the perpendicular distance of the point P from the wire, then

               ……….(10)

Now, the expression of flux density B at point P can be rewritten as,

              ……….(11)

As per the figure above,

              ……….(12)

Finally, the expression of B comes as,

     ……….(13)

This angle θ depends upon the length of the wire and the position of the point P. Say for a certain limited length of the wire, angle θ as indicated in the figure above varies from θ1 to θ2. Hence, magnetic flux density at point P due to the total length of the conductor is,

      ……….(14)

Let’s imagine the wire is infinitely long, then θ will vary from 0 to π that is θ1 = 0 to θ2 = π. Putting these two values in the above final expression of Biot Savart law, we get,

 ……….(15)

This is nothing but the expression of Ampere’s Law.

The angle between Δl⃗  and is calculated from trigonometry, knowing the distances l and x from the problem:

θ=tan−1(1m/0.01m)=89.4o.

The magnetic field at point P is calculated by the Biot-Savart law

ORIGIN OF THE BOUND CURRENTS

Physically, the bound currents on the surface of a magnetized material (and also in its volume for a non-uniform M) originate from the mis-cancellation of the microscopic currents inside the atoms which give rise to their magnetic moments.

As a model of how this works, consider a large LLL a uniformly magnetized material with M pointing in the z direction of the cube. For simplicity, let's assume the material in question is a crystal with a simple cubic lattice each tiny aaa cube occupied by a single atom, and furthermore, assume each atom has the same magnetic moment

m=a3M        …………(1)

The picture below shows a single slice of this cubic lattice along the (x; y) plane, or rather a small part of that slice:

Figure 5: Origin of the bound currents

The red loops here stand for the current loops creating the atomic magnetic moments m. We do not know the radii or even the shapes of these loops or the currents which flow through them; we do not even know if the currents are line currents or volume currents. But for our purposes all such details do not matter, all we care is the net magnetic moment m of each atom. As far as the macroscopic magnetic field B(r) is concerned, we may replace each atom with an aaa cube with the surface current

I =    which imply  K = =      …………(2)

flowing around the 4 vertical sides of the cube. Here is the picture of such a cubic model, or rather, of a small part of a single slice of the cubic lattice:

Figure 6: Origin of the bound currents

Inside each atom, the current flows counter clockwise. But when we look at the boundary between two neighbouring atoms, we immediately see that over that boundary, the currents of the two atoms flow in opposite directions. And since they have the same magnitude I=m/a2, they cancel each other. Thus, in the middle of the crystal all the atomic currents cancel each other and there is no net current. However, at the outer boundary of the crystal there is no cancellation.

Figure 7: Bound currents

Instead, there is un-cancelled current I=m/a2 flowing counter clockwise around the entire outer boundary of the crystal, or rather of single atomic layer of the crystal. The next layer on top of the layer shown on the above picture has a similar current, and so is every other layer, which makes for a surface current density.

K = = = M       …………(3)

Over the 4 vertical sides of the whole magnetized cube. In vector notations, the surface current on each side of the cube is

K = M n        …………(4)

where n is the unit vector normal to the side in question.

The above toy model explains the physical origin of the surface bound current. It does not have a volume bound current since we assumed a uniform magnetization inside the magnetic material.

To model a non-uniform magnetization we should give different atoms different magnetic moments m and hence different atomic currents. Consequently, at the boundary of two neighbouring atoms we would no longer have exact cancellation of their currents, and that would give rise to bound volume currents inside the bulk of the magnetized material. Assuming for simplicity that all atomic magnetic moments point in z directions but their magnitudes slowly depend on x and y coordinated of the atom, the net current on the boundary between two atoms neighbouring in x direction is

      …………(5)

while on the boundary between two atoms neighbouring in y direction

      …………(6)

Averaging these currents over the volume of the magnetized crystal, we get the volume bound current

…………(7)

Given: χ = –0.4 × 10‒5

H = 5 × 105 A /m

B = ? and M = ?

B = μ0(H + M) = μ0 H(1 + χ)

    = 4π × 10‒7 × 5 × 105 [1 – 0.4 × 10‒5] = 4π × 5 × 10‒2 × 0.9996 = 0.62 Wb/m2

M = χH = –0.4 × 10–5 × 5 × 105 = –2.0 A/m.

An object containing a magnetization distribution can be modelled by replacing the magnetization by bound volume and surface currents Jb and Kb. If we add in some extra free current Jf not due to the magnetization (for example, by plugging the object into the electric mains), then the total current at a point inside the object is

J=Jb+Jf          ………………(1)

Since Jb=∇×M        ………………(2)

by definition, we can write Ampère’s law as

∇×B = J         ………………(3)

∇×B = Jf + ∇×M        ………………(4)

∇× B - M)= Jf        ………………(5)

The quantity in parentheses is given the symbol H:

B - M)= H         ………………(6)

H is called the auxiliary magnetic field or sometimes just the magnetic field, with B being called the magnetic flux density. This allows a variant form of Ampère’s law:

∇×H = Jf         ………………(7)

= If         ………………(8)

Where If  is the free current enclosed by the path of integration.

One thing that is a bit worrying is that the bound surface current Kb seems to have vanished in this derivation but Jackson gets round the problem by saying that the surface integral from which Kb was defined as

  da’         ………………(9)

is zero by assuming that the magnetization M is well-behaved and localized, and we can take the surface at infinity where M=0.

He then states later that in some idealized problems, it is convenient to assume that M is discontinuous at the boundary between two objects (for example, between a magnetized object and the surrounding air), and in that case, the surface current term must be added in.

However, in any ’real’ physical situation, discontinuities never occur so the surface term doesn’t appear and the definition of H above is valid.

In any case, we can use this definition of H to calculate B more easily in some idealized situations.

we have an infinitely long cylinder of radius R with a fixed M=kr , by the bound current approach

Jb=∇×M         ………………(10)

   = k          ………………(11)

Kb=M(R)׈         ………………(12)

     =kR         ………………(13)

Note that the total bound current is zero, since the total volume current is

dr = - kR        ………………(14)

Both bound currents effectively produce solenoids, so the field outside the cylinder is zero. Inside, we have field due to the surface current, which is

Bk =          ………………(15)

and we must add to that the field due to those parts of the cylinder with a radius greater than the radius r of interest. The total current outside radius r is

dr = - k(R-r)        ………………(16)

so the total field is

Bk = - - k(R-r) = =     ………………(17)

Using H, we can take a loop of integration of radius r centred on the z axis. Since there is no free current, we get

= 0         ………………(18)

and from the symmetry of the problem we can conclude that H=0

Alternatively, we can work from the curl equation which gives ∇×H=0. This on its own isn’t enough to conclude that H=0, but we can also calculate the divergence

∇·H=∇·B−∇·M        ………………(19)

Since ∇·B=0 always, and by direct calculation we can show that ∇·M=0 in this case, we have both the curl and divergence of H as zero, so H must be zero. From that, we can conclude immediately from the definition of H that B=μ0M.

In homogeneous media, electromagnetic quantities vary smoothly and continuously. At a boundary between dissimilar media, however, it is possible for electromagnetic quantities to be discontinuous. Continuities and discontinuities in fields can be described mathematically by boundary conditions and used to constrain solutions for fields away from these boundaries. In this section, we derive boundary conditions on the magnetic field intensity H.

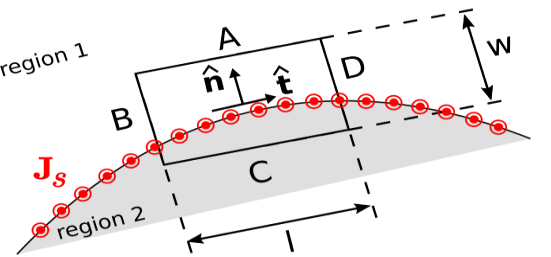
Figure 4: Determining the boundary condition on H at the smooth boundary between two material regions.

To begin, consider a region consisting of only two media that meet at a smooth boundary as shown in above Figure. The desired boundary condition can be obtained directly from Ampere’s Circuital Law

∮C H⋅dl= Iencl         ……….(1)

where C is any closed path and Iencl is the current that flows through the surface bounded by that path in the direction specified by the “right-hand rule” of Stokes’ theorem.

Let C take the form of a rectangle centered on a point on the boundary as shown in Figure, perpendicular to the direction of current flow at that location.

 Let the sides A, B, C, and D be perpendicular and parallel to the boundary. Let the length of the parallel sides be l, and let the length of the perpendicular sides be w.

Now we apply Ampere’s Circuital Law, We must integrate in a counter-clockwise direction in order to be consistent with the indicated reference direction for Js

Thus:

∮H⋅dl=∫A H⋅dl+∫B H⋅dl+∫C H⋅dl+∫D H⋅dl=Iencl

Now we let w and l become vanishingly small while maintaining the ratio l/w and keeping C centered on the boundary. In this process, the contributions from the B and D segments become equal in magnitude but opposite in sign; i.e.,

∫B H⋅dl +∫D H⋅dl →0         ………(2)

This leaves

∫A H⋅dl+∫C H⋅dl=Iencl

Let us define the unit vector (“tangent”) as shown in Figure 1. Now we have simply:

H1⋅(− Δl)+H2⋅(+ Δl)=Iencl        ………(3)

Where H1 and H2 are the fields evaluated on the two sides of the boundary, and Δl→0 is the length of sides A and C. As always, Iencl (units of A) may be interpreted as the flux of the current density Js (units of A/m) flowing past a line on the surface having length Δl (units of m) perpendicular to , where   is the normal to the surface, pointing into Region 1. Stated mathematically:

Iencl →Js ⋅(Δl  )         ………(4)

Before proceeding, note this is true regardless of the particular direction we selected for ; it is only necessary that  be tangent to the boundary. Thus,  need not necessarily be in the same direction as Js. Now Equation (3) can be written:

H1⋅(− Δl)+H2⋅(+ Δl)=Js ⋅(Δl  )      ………(5)

Eliminating the common factor of Δl and arranging terms on the left:

(H2−H1)⋅ = Js ⋅( )        ………(6)

The right side may be transformed using a vector identity (A⋅(B×C)=B⋅(C×A)=C⋅(A×B) to obtain:

(H2−H1)⋅ = Js)         ………(7)

Equation (7) is the boundary condition we seek. We have found that the component of (H2−H1) (the difference between the magnetic field intensities at the boundary) in any direction tangent to the boundary is equal to the component of the current density flowing in the perpendicular direction Js).

A discontinuity in the tangential component of the magnetic field intensity at the boundary must be supported by surface current flowing in a direction perpendicular to this component of the field.

An important consequence is that If there is no surface current, then the tangential component of the magnetic field intensity is continuous across the boundary.

It is possible to obtain a mathematical form of the boundary condition that is more concise and often more useful than Equation (7).

This form may be obtained as follows. First, we note that the dot product with respect to ton both sides of Equation (7) means simply “any component that is tangent to the boundary.” We need merely to make sure we are comparing the same tangential component on each side of the equation.

For example ×(H2−H1) is tangential to the boundary, since is perpendicular to the boundary and therefore any cross product involving will be perpendicular to . The corresponding component of the current density is ×(×Js),

so Equation (7) may be equivalently written as follows:

×(H2−H1)= ×(×Js)        ………(8)

Applying a vector identity (A×(B×C)=B(A⋅C)−C(A⋅B) to the right side of Equation (8) we obtain:

××Js= (.Js) - Js.) =(0)-(1)Js = - Js

Therefore:

× (H2−H1) = - Js        …………(9)

The minus sign on the right can be eliminated by swapping H2 and H1 on the left, yielding

× (H1−H2) = - Js        ………...(10)

This is the form in which the boundary condition is most commonly expressed.

It is worth noting what this means for the magnetic field intensity B. Since B=μH

In the absence of surface current, the tangential component of B across the boundary between two material regions is discontinuous if the permeabilities are unequal.

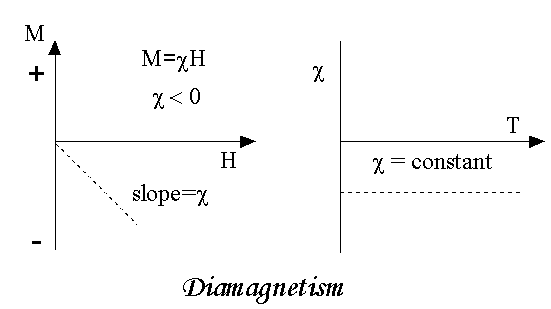
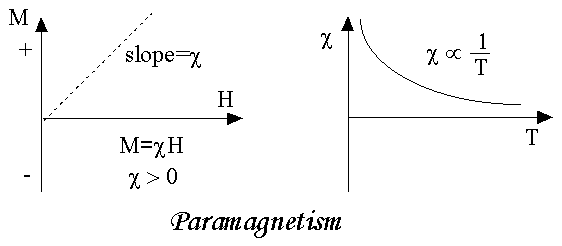
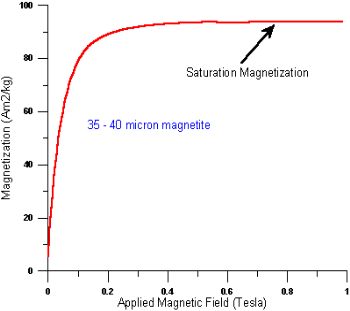
If H is the applied magnetizing field intensity and M is the amount of magnetization of the material,

Then χ =

χ = 0 in vacuum

χ = +ve for paramagnetic and Ferro magnetic materials

χ = -ve for diamagnetic materials

Units: It has no units.

We know  Induced Magnetic Field B = μ0(H+M)

Where H is the external applied magnetic field and M is the magnetization produced inside the specimen.

When the specimen is in superconducting state B=0 (Meissner effect)

B = μ0(H+M)

0 = μ0(H+M)

H= -M

χ = H/M = -1

Thus the material is act as a perfectly diamagnetic because for diamagnetic material susceptibility χ = -1

Also χ = μr -1

μr = -1+1 =0

Hence proved susceptibility of superconductor is -1 and relative permeability is zero.

Hsat Tesla

T range (K)

χ 10-8m3/kg

paramagnets

>10

<<100

~50

ferromagnets

~1

~300

1000-10000

=

Magnetization, Bound Currents, and the H Field. In magnetic materials, atoms and molecules may have non-zero average magnetic moments ⟨m⟩. Such magnetic moments are usually induced by external magnetic fields, but in permanent magnets they can remain long after the external field is switched off. One way or the other, the atomic/molecular magnetic moments lead to macroscopic magnetization.

M=      …………(1)

Here we shall explore the macroscopic magnetic field B(x; y; z) due to such magnetization. Let's start with the vector potential A(x; y; z) due to a single magnetic dipole m,

  …………(2)

By the superposition principle, the vector potential of a bunch of magnetic dipoles is a sum of potentials like (2)

  …………(3)

Likewise, for a continuous distribution of dipoles with macroscopic magnetization M(x; y; z),we have

  …………(4)

To simplify this expression, we note that

    …………(5)

and then integrate by parts:

Applying these formulae to the integrand of eq. (4), we arrive at

…………(7)

Moreover, the second term on the RHS can be rewritten as a surface integral, for any vector field T(r) and any volume V with surface S,

…………(8)

Where n(r) is a unit vector normal to the surface S at point r. In the present context, M(r′)/ plays the role of T(r′), V is the volume occupied by the magnetic material and S is its outer surface. Thus altogether, the vector potential (7) becomes

…………(9)

which has the form of a vector potential created by the volume current

Jb(r′) =∇M(r′)        ………….(10)

and the surface current

Kb(r′) =M(r′)n(r′)        ………….(11)

indeed, in terms of these current, the potential (9) becomes

The currents (10) and (11) are called the bound currents, by analogy with the bound charges in a dielectric.