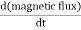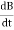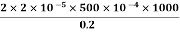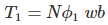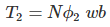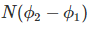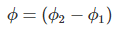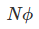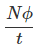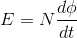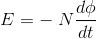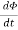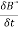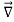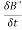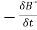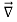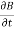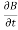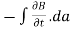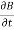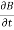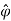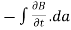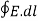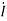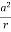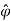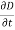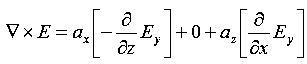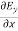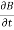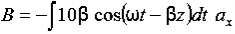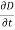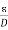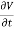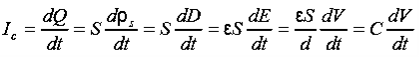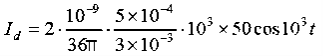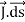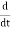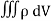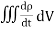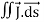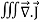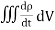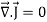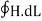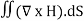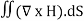Given

When there is a changing magnetic field through a coil, it causes an induced emf in the coil, which is based on the Faraday's law of electromagnetic induction. Further, the induced emf is related to the induced electric field along the circumference of the coil.

Magnetic field inside the solenoid, B =5.0×t T

Induced electric field at radial distance (from the axis of solenoid) r = 2.0 m is E =11 V/m

Radius (R) of solenoid =?

The induced electric field at the radial distance r from the axis of the solenoid is expressed as:

E×(2πr) =

E×(2πr) =

E×(2×r) =R2

E×(2×r) = R2

11×(2×2) =R2×5

R= 2.966 3.0 m

The induced emf will be given by
emf= ​
          = ​
          =
          =
          =10×10−3V=10 mV

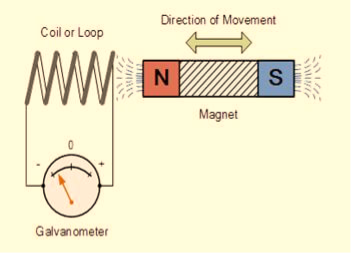
Position of magnet

Deflection in galvanometer

Magnet at rest

No deflection in the galvanometer

Magnet moves towards the coil

Deflection in galvanometer in one direction

Magnet is held stationary at same position (near the coil)

No deflection in the galvanometer

Magnet moves away from the coil

Deflection in galvanometer but in the opposite direction

Magnet is held stationary at the same position (away from the coil)

No deflection in the galvanometer

Consider, a magnet is approaching towards a coil. Here we consider two instants at time T1 and time T2. Coil has N number of turns.

Flux linkage with the coil at time,

        ………..(1)

Flux linkage with the coil at time,

        ………..(2)

Change in flux linkage,

         ………..(3)

Let this change in flux linkage be,

        ………..(4)

So, the Change in flux linkage

          ………..(5)

Now the rate of change of flux linkage

          ………..(6)

Take derivative on right-hand side we will get as N is number of turns of coils which is constant so taken out of derivative, we get

         ………..(7)

The rate of change of flux linkage

         ………..(8)

Where E is induced emf.

But according to Faraday’s law of electromagnetic induction, the rate of change of flux linkage is equal to induced emf.

        ………..(9)

Considering Lenz’s Law

Where:

• Flux Φ in Wb = B.A
• B = magnetic field strength
• A = area of the coil

Time-varying magnetic field will always produce an electric field. According to the faraday’s law “Whenever there are n-turns of conducting coil in a closed path which is placed in a time-varying magnetic field, an alternating electromotive force gets induced in each and every coil.” This is given by Lenz’s law. Which states that An induced electromotive force always opposes the time-varying magnetic flux.

When two coils with N number of turns; A primary coil and Secondary coil. The primary coil is connected to an alternating current source and the secondary coil is connected in a closed loop and is placed at a small distance from the primary coil. When an AC current passes through the primary coil, an alternating electromotive force gets induced in the secondary coil.

Mathematically it is expressed as –

Alternating emf, emf=−Ndϕdt   ——–(1)

Where,

N is the number of turns in a coil

𝜙 is the scalar magnetic flux.

The negative sign indicates that the induced emf always opposes the time-varying magnetic flux.

Let N=1,

⇒ emf = −  ——-(2)

Here, the scalar magnetic flux can be replaced by –

ϕ=∬B⃗ .ds⃗  ——–(3)

Substitute equation (3) in (2)

emf= − ∬B⃗ .ds⃗ 

Which is an partial differential equation given by-

emf = ∬− ds⃗     ———–(4)

The alternating electromotive force induced in a coil is basically a closed path

⇒emf = ∮E⃗ .dl⃗   ——-(5)

Substituting equation (5) in (4) we get-

⇒ ∮E⃗ dl⃗ = ∬− ds⃗ —–(6)

The closed line integral can be converted into surface integral using Stoke’s theorem. Which states that “Closed line integral of any vector field is always equal to the surface integral of the curl of the same vector field”

⇒∮E⃗ dl⃗ =∬(×E⃗ ).ds⃗    ———(7)

Substituting equation (7) in (6) we get-

⇒=∬(×E⃗ ).ds⃗    = ∬− ds⃗     ———(8)

The surface integral can be cancelled on both sides. Thus, we arrive at

× E⃗ =

Hence, we can conclude that the time-varying magnetic field will always produce an electric field.

This is the differential form of faraday’s law. It is also known as Maxwell-Faraday Equation.

For the static magnetic field, which states that Static electric field vector is an irrotational vector.

Static field implies the time-varying magnetic field is zero,

⇒ =0 ⇒× E⃗ =0

Hence it is an irrotational vector.

Faraday’s law in differential form is

∇×E = −        …………(1)

There is a similarity to Ampère’s law, which says

∇×B = μ0 J        ………… (2)

Considering only electric fields generated from changing magnetic fields (and not those generated by free charges), we then have∇·E=0, since there is no free charge.

For magnetic fields, ∇·B=0 always. Once we specify both the curl and divergence of a vector field, the field is deter-mined uniquely (up to a constant), so Faraday’s law is formally equivalent to Ampère’s law, except that curl is determined by

− Instead of μ0 J.

In particular, we can use the right hand rule to determine the direction of E if we know − and we can use Ampèrian loops to calculate E in those problems where the symmetry makes the calculation easier. There is one important difference between Faraday’s and Ampère’s law, however. Ampère’s law assumes that the currents J are steady, that is, that there is no dependence on time. Faraday’s law clearly does depend on time, in that an electric field is generated only if the magnetic field is changing.

 In differential form, this doesn’t pose a problem, since both sides of the equation refer to a single point(x,y,z). However, in its original integral form:

=        ………… (3)

The t variable is assumed to be the same at all points in the integrals. If we choose some enormous loop for the integral on the left, then any change in B, even one in some small, remote corner of the area enclosed by the loop, is implicitly assumed to affect E instantaneously around the entire loop.

This is a problem inherent in all non-relativistic physics. In Newton’s gravitational theory, for example, no provision is made for any travel time from one mass to the other; if the sun were to suddenly lose half its mass, say, the effect would be felt at the Earth immediately. In reality, of course, nothing can travel faster than the speed of light, so changes in one part of a system will not be felt at other parts until some signal informing these remote parts of the change has reached them.

In the case of electromagnetism, the signal speed happens to be exactly that of light, so when we apply Faraday’s law in integral form, we really need to take this into account. In practice, when we’re dealing with finite electrical circuits or situations within an Earth-bound laboratory, the distances are usually so short that we can make the approximation that the travel time is zero. This is known as the quasistatic approximation. 

As a simple example, suppose we have an infinite solenoid with n turns per unit length and of radius a, carrying a time-dependent current I(t). The fact that the solenoid is infinite means that the quasistatic approximation could well break down for large distances, but we’ll do the calculation anyway and see what we get.

Inside the solenoid, the field is

B=nμ0I(t)         …………(4)

so

− =−nμ0 (t)        ………..(5)

Note: (t) is I dot i.e. derivative of I

Using the analogy between Ampère’s and Faraday’s laws, since the direction of −  is −z, we can apply the right-hand rule to find that the induced electric field is circumferential and in the − direction (that is, clockwise, looking towards −z). The magnitude of E is obtained by integrating the field around a circle of radius r < a:

= 2πrE = =−πr2nμ0 (t)     ………..(6)

E=− rnμ0 ̇I(t)         ………..(7)

Outside the solenoid, B is always zero, so there is no contribution to E here. A circular integration path at a distance r > a still contains the flux inside the solenoid, so

= 2πrE = =−πa2nμ0 (t)     ………..(8)

E=− rnμ0 ̇I(t)   

Maxwell’s four equations are given by

∇·E = ρ/ε0        (1)

∇×E = −∂B/∂t        (2)

∇×H = J + ∂D/∂t       (3)

∇·B = 0        (4)

These equations illustrate the unique coexistence in nature of the electric field and the magnetic field. The first two equations give the value of the given flux through a closed surface, and the second two equations give the value of a line integral around a loop. In this notation,

∇=(∂/∂x, ∂/∂y, ∂/∂z)

E is the electric vector

B is the magnetic induction

ρ is the electric charge density

j is the electric current density

ε0 is the permittivity of free space

c is the speed of light.

In addition to Maxwell equations, the following identities are useful:

J =  σE         (5)

D = εE         (6)

B = μH         (7)

Here,

 D is the electric displacement

H is the magnetic vector

 σ is the specific conductivity

ε is the dielectric constant (or permittivity)

 μ is the magnetic permeability

E at a TV receiver in free space= 5.0 cos (t-y) az, V/m

Electric flux density

D =0E = 50cos (t-y) az, V/m

The displacement current density

Jd =

=

Jd=-50sin (t-y) az, V/m2

The conduction current density,

Jc =E

=2.0 x 103(mho) /cm

= 2 x 105mho /m

Jc= 2 x 105x 5 cos (t-y) az

Jc= 106cos (t-y) az V/m2

E = 10 sin (t-y) ay, V/m

D =0E,

0= 8.854 x 10-12 F/m

D = 100sin (t-y) ay, C/m2

Second Maxwell’s equation is

x E = -B

That is,

or

As Ey= 10 sin (t-z) V/m

= 0

Now,x E becomes

x E = - ax

= 10 cos (t-z) ax

= -

D =E

Jd = =

Hence,

Id = Jd. S

=

=

which is the same as the conduction current, given by

= 147.4 cos 103t nA

When electromagnetic wave travels in space, it carries energy and energy density is always associated with electric fields and magnetic fields.

The rate of energy travelled through per unit area i.e. the amount of energy flowing through per unit area in the perpendicular direction to the incident energy per unit time is called Poynting vector.

Mathematically Poynting vector is represented as

= =( )   (i)

The direction of Poynting vector is perpendicular to the plane containing   and . Poynting vector is also called as instantaneous energy flux density. Here rate of energy transfer is perpendicular to both   and.  It represents the rate of energy transfer per unit area.

UNIT

Its unit is W/m2.

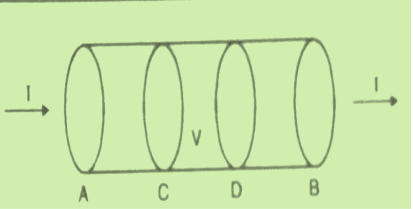
Equation of continuity

Consider a closed surface S enclosing a Volume V through which currents are flowing. Let I be the current passing through the surface at any time t. Consider a small area of the closed surface. The outward current flowing through    at a time t is

Figure 3: Current density through surface S

dI =       …………..(1)

the total current flowing out through the closed surface S at time t is

I =       …………..(2)

Suppose is ρ the Volume Charge density of charges inside the surface S. Then the total charge inside the Volume V is

q =       …………..(3)

Since the current is flowing outward is it mean that charge within the enclosed surface is decreasing with time. The time rate of decrease of charge is

= -       …………..(4)

The negative sign shows that the charge inside the surface S is decreasing with time. The above equation can be written as

= -       …………..(5)

Since the charge is conserved, the current flowing outward through the closed surface must be equal to the rate of decrease of charge. Thus 

I =

Using equation (2) and (5), it becomes

= -       …………..(6)

According to divergence theorem

= dV

Using this result in equation (6) we obtain

dV = -   

This equation holds good for arbitrary volumes. Therefore the integrands must be equal. Hence  

=0 …………..(7)

This equation is called equation of continuity. It is the mathematical statement of law of conservation of charge. 

Special case

Consider a conductor AB through which a steady current I is flowing. The current I is said to be steady if charge is flowing per unit time through any two any sections C and D is the same. This means that the total amount of charge entering the volume V through C is equal to the charge leaving the volume V through D. Thus there is no change in the volume charge density in the volume V with time i.e.

=0

Figure 4: Current through conductor AB

We may define steady current as that current in which the charge density is independent of time.

Using equation (7) we obtain

This is known as the equation of continuity for steady currents.

Statement of Ampere’s circuital law (without modification). It states that the line integral of the magnetic field H around any closed path or circuit is equal to the current enclosed by the path.

That is                                   ∫ H. dL=I

Let the current is distributed through the surface with a current density J

Then                                                I=

This implies that                           =                          (1)

Apply Stoke’s theorem to L.H.S. of equation (1) to change line integral to surface integral,

That is                                =

Substituting above equation in equation (9), we get

=

As two surface integrals are equal only if their integrands are equal

Thus,                                            ∇ x H=J                                          (2)

This is the differential form of Ampere’s circuital Law (without modification) for steady currents.

Take divergence of equation (2)

∇.(∇xH)= ∇.J

As divergene of the curl of a vector is always zero ,therefore

∇.( ∇xH)=0

It means                                     ∇.J=0

Now, this is equation of continuity for steady current but not for time varying fields, as equation of continuity for time varying fields is

∇ .J = –

If we do some simple mathematical tricks to Maxwell's Equations, we can derive some new equations. Here we'll look at the continuity equation, which can be derived from Gauss' Law and Ampere's Law.

We will start with a vector identity which states that the divergence of the curl of any vector field is always zero:

∇.( ∇xH)=0        …………(1)

If we apply the divergence to both sides of Ampere's Law, then we obtain:

∇.( )= ∇.( ∇x H)=0 

  = - ∇.J        …………(2)

If we apply Gauss' Law to rewrite the divergence of the Electric Flux Density (D), we have derived the continuity equation

∇.J = –         …………(3)

The left side of the equation is the divergence of the Electric Current Density (J). This is a measure of whether current is flowing into a volume (i.e. the divergence of J is positive if more current leaves the volume than enters).

Recall that current is the flow of electric charge. So if the divergence of J is positive, then more charge is exiting than entering the specified volume. If charge is exiting, then the amount of charge within the volume must be decreasing. This is exactly what the right side is a measure of how much electric charge is accumulating or leaving in a volume. Hence, the continuity equation is about continuity - if there is a net electric current is flowing out of a region, and then the charge in that region must be decreasing. If there is more electric current flowing into a given volume than exiting, than the amount of electric charge must be increasing.