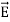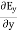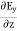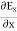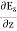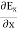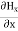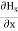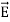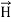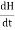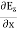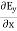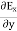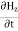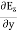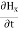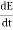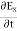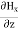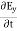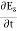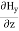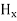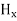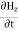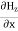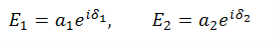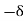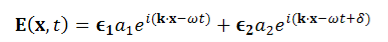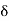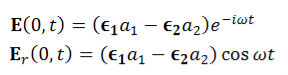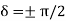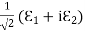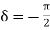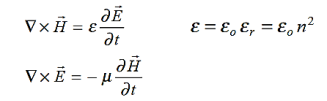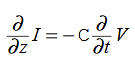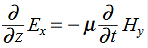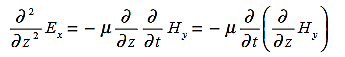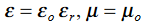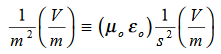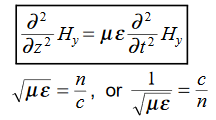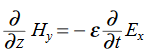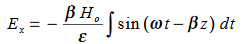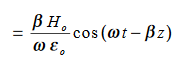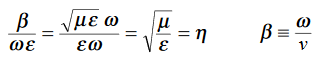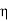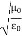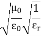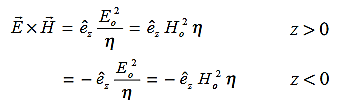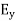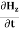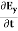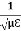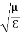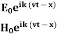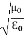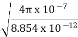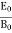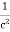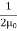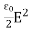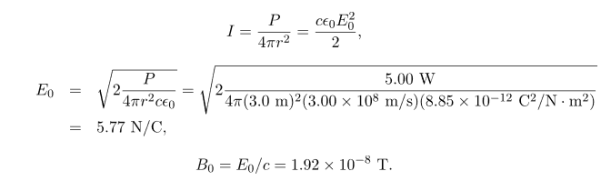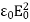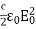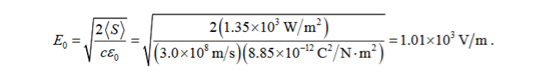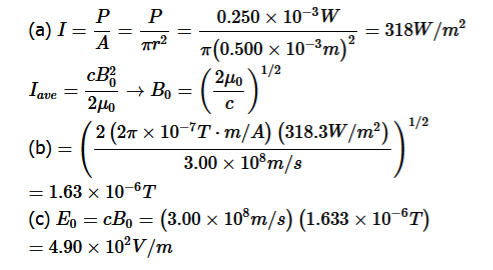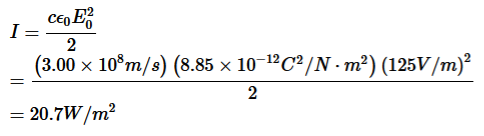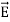undefined | unit 4 electromagnetic wave

PHY

UNIT-4ELECTROMAGNETIC WAVESQ1) Prove why electromagnetic waves are transverse in nature?OrProve the absence of longitudinal component in em wave?A1) In an electromagnetic wave, electric and magnetic field vectors are perpendicular to each other and at the same time are perpendicular to the direction of propagation of the wave. This nature of electromagnetic wave is known as Transverse nature.Maxwell proved that both the electric and magnetic fields are perpendicular to each other in the direction of wave propagation. He considered an electromagnetic wave propagating along positive x-axis. When a rectangular parallelepiped was placed parallel to the three co-ordinate axis, the electric and magnetic fields propagate sinusoidal with the x-axis and are independent of y and z-axis.A wave in which the values of variable are constant in a plane perpendicular to the direction of propagation of the wave is called plane wave. These planes may also termed as wave fronts.In this section we will study the variation of field of

and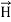

of an em plane wave with space and time.Variation with Space

First, we will consider the variation with space. Suppose a plane em wave is propagating along x axis. Then the values of the field vectors and will be constant on any plane parallel to YZ plane. That is:

For

= = = = 0 …………(1)

For

= = = = 0 …………(2)

From Maxwell’s equation for free space, we have

∇.E=0

Therefore

++ =0

Which gives

=0 …………(3)

Also From Maxwell’s equation for free space, we have

∇.B=0 we have ∇.H=0 as B = μH

Hence

++ =0

Which gives

=0 …………(4)

The equation (3) and (4) show that there is no variation of 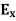and alo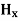ng the X axis. In other words, there is no variation in the longitudinal component of and .

Time Variation of

and

The Maxwell’s equation in free space can be written as:

∇ x E= -dB/dt or ∇ x E= -μ because B = μH

Comparing the rectangular components, we find:

- = -μ …………(5)

- = -μ …………(6)

- = -μ …………(7)

Applying the condition listed in equation (1), from equation (5), we find:

- =0

=0 …………(8)

Again using Maxwell’s equation for free space is:

∇ x H= = Ɛ

Comparing the rectangular components, we can write:

- = Ɛ …………(9)

- = Ɛ …………(10)

- = Ɛ …………(11)

Again using the conditions listed in equation (2) gives:

- = 0

= 0 …………(12)

From equation (8) and (12), we find that there is no variation in the values of and with time. That is and neither vary with space nor with time. So at the most they can have constant value. But the constant values of and contribute nothing towards the wave because for the wave the field vectors must possess oscillatory nature. This shows that there is no longitudinal component of the field vectors in the electromagnetic wave. In other words, for the purpose of discussing of the wave nature, we may put =0

Now from equation 6 and 7 by putting = 0, we find:

= μ …………(13)

= - μ …………(14)

Similarly putting =0 in equation (10) and (11) we find:

= - Ɛ …………(10)

= Ɛ …………(11)

These relations show that in the em values and are related to each other. Also and are related to each other, and their time or space variation are not zero. From this we conclude that the em wave is transverse in nature

Q2) Derive electromagnetic wave equation?A2) Wave is nothing but a pattern of disturbance which propagates and carry energy with it. You can produce a wave on a rope by moving one end of the rope up and down. The wave produces on rope needs a medium to propagate and here medium is rope itself. This type of waves is known as mechanical waves. But in the case of Electromagnetic waves, they don't need a medium to propagate. Electromagnetic waves are waves that are created as a result of variations of electric field and a magnetic field. Or we can say that Electromagnetic waves are nothing but changing magnetic and electric fields. Electromagnetic waves are also known to be solutions of Maxwell's equations. And Maxwell's equations are the fundamental equations of electrodynamics. Electromagnetic waves can transmit energy and travel through a vacuum. Light waves are examples of electromagnetic waves. Generally, Electromagnetic waves are shown by a sinusoidal graph.

Figure 1: Electromagnetic wavesAs shown in figure Electromagnetic waves consist of time-varying electric and magnetic fields and they are perpendicular to each other and these both fields are also perpendicular to the direction of propagation of waves.

Maxwell’s four equations are given by

∇·E = ρ/ε0 (1)

∇×E = −∂B/∂t (2)

∇×H = J + ∂D/∂t (3)

∇·B = 0 (4)

These equations illustrate the unique coexistence in nature of the electric field and the magnetic field. The first two equations give the value of the given flux through a closed surface, and the second two equations give the value of a line integral around a loop. In this notation,

∇=(∂/∂x, ∂/∂y, ∂/∂z)

E is the electric vector

B is the magnetic induction

ρ is the electric charge density

j is the electric current density

ε0 is the permittivity of free space

c is the speed of light.

In addition to Maxwell equations, the following identities are useful:

J = σE (5)

D = εE (6)

B = μH (7)

Here,

D is the electric displacement

H is the magnetic vector

σ is the specific conductivity

ε is the dielectric constant (or permittivity)

μ is the magnetic permeability

Free space or non-conducting medium. We know that non conducting medium means no current so conductivity is zero i.e. σ=0

So current density J=σE will also become zero as σ=0 Also free space means no charges which leads to ρ=0. These points mentioned below.

(a) No condition current i.e σ=0, thus J=0 ( J=σE)

(b) No charges (i.e ρ=0)

For the case of no charges or currents, that is, j = 0 and ρ = 0, and a homogeneous medium. Using these the Maxwell equation can rewritten as

∇.D=0 or ∇.E=0 as ρ=0 (12)

∇ x E= -dB/dt or ∇ x E= -μ dH/dt because B = μH (13)

∇ x H=d D/dt or ∇ x H = ε dE/dt (J=0) and D = εE (14)

∇.B=0 (15)

WAVE EQUATION IN TERMS OF ELECTRIC FIELD INTENSITY, E

Now taking curl of second Maxwell’s equation (13) ,we get

∇ x(∇ x E)=- μ d/dt (∇ x H)

Applying standard vector identity, that is [∇ *(∇*E)=∇(∇.E)-∇2E] on left hand side of above equation, we get

∇ (∇ .E)-∇2E= -μ d/dt (∇ x H) (16)

Substituting equations (13) and (14) in equations (16) ,we get

-∇2E= – με d/dt (dE/dt)

Or ∇2E=με d 2 E/dT2 (17)

Equation (17) is the required wave equation in terms of electric field intensity, E for free space . This is the law that E must obey.

WAVE EQUATION IN TERMS OF MAGNETIC FIELD INTENSITY, H

Take curl of fourth Maxwell’s equation (14) ,we get

∇x(∇xH)=ε d/dt(∇xE)

Applying standard vector identity that is

[∇*(∇*H)=∇ (∇.H)-∇2H]

On left side of above equation , we get

∇(∇.H)-∇2H= ε d/dt(∇xE) (18)

Substituting equations (14) and (13) in equation(18) ,we get

-∇2H= – μεd/dt(dH/dt)

∇2H=με d2H/dt2 (19)

Equations (19) is the required wave equation in terms of magnetic field intensity, H and this is the law that H must obey

For vacuum μ=μ0 and ε=ε0, equations (17) and (19) will become

∇2 E=μ0ε0 d2E/dt2 (20)

And ∇2H= μ0ε0 d2H/dt2 (21)

This leads to an expression for the velocity of propagation

From equation both equations (20) and (21) have the form of the general wave equation for a wave

(x,t) traveling in the x direction with speed v. Equating the speed with the coefficients, we derive the speed of electric and magnetic waves, which is a constant that we symbolize with “c”

It is useful to note that in vacuum

c2=1/ε0μ0

Where μ0 is the permeability of free space

Let us rewrite the equation (20) and (21) for one dimension.

Or d 2 E/dx2 = μ0ε0 d 2 E/dt2 (22)

d2H/dx2 = μ0ε0 d2H/dt2 (23)

The simplest solutions to the differential equations (22) and (23) are sinusoidal wave functions:

E(x) = Emax cos(kx-t) (24)

B(x) = Bmax cos(kx-t) (25)

where k = 2π/λ is the wavenumber , ω = 2πƒ is the angular frequency, λ is the wavelength, f is the frequency and ω /k=f=v= c.

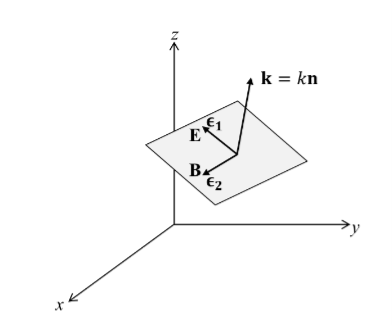
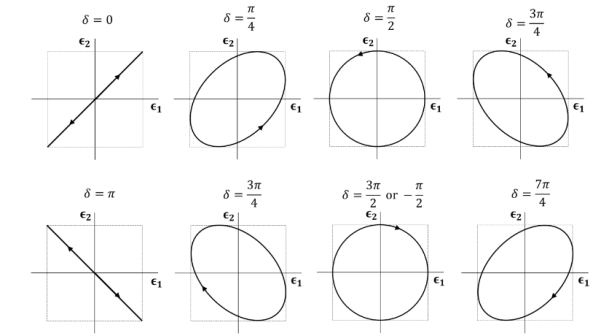
Q3) Discuss the polarization of em wave? A3)

There is more to be said about the complex vector amplitudes Ɛ and B. We introduce a right-handed set of orthogonal unit vectors (Ɛ1, Ɛ2, n), as shown in Figure, where we take n to be the propagation direction of the plane wave. In general, the electric field amplitude Ɛ can be written as

where the amplitudes and are arbitrary complex numbers. The two plane waves

and

if the n index of refraction is real, Ɛ and B have the same phase) are said to be linearly polarized with polarization vectors Ɛ1 and Ɛ2 .Thus the most general homogeneous plane wave propagating in the direction k=kn is expressed as the superposition of two independent plane waves of linear polarization:

Figure 2: Polarization of em waves

It is convenient to express the complex components in polar form. Let

Then, for example,

that is 1 is the phase of the E-field component in the Ɛ1-direction. It is no restriction to let

21 1=0

Since 1=0 merely dictates a certain choice of the origin of t. With this choice,

or the real part is

The E -field is resolved into components in two directions, with real amplitudes a1 and a2, which may have any values. In addition the two components may be oscillating out of phase by , that is, at any given point x, the maximum of E in the Ɛ1-direction may be attained at a different time from the maximum E of in the –direction Ɛ2.

A detailed picture of the oscillating E-field at a certain point , e.g. x=0,, is best seen by considering some special cases.

Linearly polarized wave

If E1 and E2 have the same phase , i.e.,

represents a linearly polarized wave, with its polarization vector

Ɛ = Ɛ1cosθ + Ɛ2sinθ

with θ=tan-1 (a2/a1)and a magnitude E= as shown in Figure.

Figure 3: field of a linearly polarized wave

If a1 =0 or a2=0 , we also have linear polarization. For,

is again linearly polarized.

Elliptically polarized wave

If E1 and E2 have different phases, the wave of Eq. 7.27 is elliptically polarized. The simplest case is circular polarization. Then a1 = a2 and :

At a fixed point in space, the fields are such that the electric vector is constant in magnitude, but sweeps around in a circle at a frequency ω, as shown in Figure

For += , the tip of the E-vector traces the circular path counter clockwise. This wave is called left circularly polarized (positive helicity) in optics.

For ,), same path but traced clockwise, then the wave is called right circularly polarized (negative helicity). For other values of , we have elliptical polarization for the trace being an ellipse.

Figure 4: Trace of the tip of the E-vector (a1 = a2) at a given point in space as a function of time. The propagation direction is point toward us. The traces for and are linearly polarized. The traces for and are left and right circularly polarized, respectively.

Q4) Given E = 10 sin (t-y) ay V/m, in free space, determine D, B and H.A4)

E = 10 sin (t-y) ay, V/m

D =0E,

0= 8.854 x 10-12 F/m

D = 100sin (t-y) ay, C/m2

Second Maxwell’s equation is

x E = -B

That is,

As Ey= 10 sin (t-z) V/m

= 0

Now,x E becomes

x E = - ax

= 10 cos (t-z) ax

= -

Q5) If the electric field strength, E of an electromagnetic wave in free space is given by E = 2 cos  (t -

) ay V/m,Find the magnetic field, HA5)

We have

B/t =-x E

Thus

Also

Q6) Write down solution for plane electromagnetic waves in vacuum?A6) In an electromagnetic wave, electric and magnetic field vectors are perpendicular to each other and at the same time are perpendicular to the direction of propagation of the wave. This nature of electromagnetic wave is known as Transverse nature.Maxwell proved that both the electric and magnetic fields are perpendicular to each other in the direction of wave propagation. He considered an electromagnetic wave propagating along positive x-axis. When a rectangular parallelepiped was placed parallel to the three co-ordinate axis, the electric and magnetic fields propagate sinusoidal with the x-axis and are independent of y and z-axis.A wave in which the values of variable are constant in a plane perpendicular to the direction of propagation of the wave is called plane wave. These planes may also termed as wave fronts.Solutions of Maxwell’s Equations - Uniform Plane Waves

The sources of time varying electromagnetic fields are time varying charges and currents, whether man-made or naturally occurring. However, examination of Maxwell’s equations shows that, even in empty space (with no sources), and fields cause each other. This means that, although these fields must originate in source regions, they can propagate through source-free regions. Because solutions in source regions are very hard to obtain, let us consider what kind of fields can exist in source-free regions.

These equations are still very complicated (4 different partial derivatives). Let’s try to find simple solutions. We do this by making assumptions. After finding simplest solutions, we:

(i) Find what kind of source would generate this type of field (waves).

(ii) Show that these simple solutions are useful approximations to real electromagnetic waves.

Assumption for Solution:

Can we find a solution such that:

1.) No variation exists in x and y directions.

2.) or also is oriented along one of the axes.

Ampere’s Law becomes:

or, with our assumptions:

Compare for transmission line:

In a similar manner,

………….(1)

Faraday’s Law becomes:

………….(2)

Thus, if is only in the direction, then is only in the .If we differentiate (2) with respect to z, we get:

Substitute from (2),

We get

This is called the wave equation.

Compare for transmission line: (same).

We will assume dielectric media; lossless:

Dimensional analysis:

In the units we are using:

By exactly the same method, we also get:

For example, the same equation is true for and . Thus, and must have the same type of functional dependence. This wave equation still has many possible solutions. In fact, it can be shown by direct substitution that

are the solutions

t is important to note that f1 and f2 can be any function.

The field we find directly from the equation:

Suppose

…………(3)

Differentiate (3) with respect to z

…………(4)

Integrate with respect to time

…………(5)

This leads to a new quantity that relates the electric and magnetic fields:

Rewriting:

Units of = = = Ω

0 = Impedance of free space = =377 Ω

= impedance of a lossless dielectric = = =

Note that and are in time phase and space quadrature

The directions of the vectors are such that:

This vector , always points in the direction of propagation. These types of waves are called Uniform Plane Electromagnetic Waves.

“Plane” refers to the fact that, at any instant in time, the surfaces of constant phase are planes (here, constant). “Uniform” means no variation in transverse direction. The wave derived here is one oscillating at a single frequency. The frequency is determined by the source. If the source has multiple frequencies, so will the wave. In communications, modulating a carrier wave results in multiple frequencies. But before we can study such fields, we must thoroughly understand single frequency sinusoidal waves. Q7) Derive relation between electric and magnetic fields of an electromagnetic wave?A7)

We know that wave equations are given by

∇2 E=με d2E/dt2 …………..(1)

And ∇2H= με d2H/dt2 …………..(2)

The electric and magnetic vectors in an em waves are given by:

= E0eik (vt-x) …………..(3)

= H0eik (vt-x) …………..(4)

It is evident therefore that:

Both electric and magnetic vectors oscillate sinusoidally with the same frequency and in the same phase with each other.
The planes of their oscillations are mutually perpendicular and also perpendicular to the direction of propagation of the waves (transverse wave).
The disturbance corresponding to both the electric and magnetic vectors propagate with the same speed and the waves corresponding to each have the same length.
The relation between their time and space variations is given by:

= - μ …………..(5)

and

= - Ɛ …………..(6)

Substitute the values of and in equation (5), we find :

-ik E0eik (vt-x) =- μ (ikv) H0eik (vt-x)

Which gives

E0 =- μvH0

But v =

E0 = μ x H0

E0 = H0

= = =

That is the relation between the values of the electric and magnetic vectors as determined by the relative values μ and Ɛ. In other words, the ratio of the electric and magnetic vectors is directly proportional to the square root of the ratio of μ and Ɛ.

For free space or vacuum

= = = = 376.73 377

E0 =377 H0 or E =377H

It shows that the values of electric vector at any instant in the em wave are about 377 times the values of magnetic vector. It is because of this reason that while discussing the behaviour of light as em wave, we prefer the use of the electric vector.

Q8) Derive relation for energy carried by electromagnetic waves?A8)

A wave’s energy is proportional to its amplitude squared. This is true for waves on guitar strings, for water waves, and for sound waves. In electromagnetic waves, the amplitude is the maximum field strength of the electric and magnetic fields. So the energy of electromagnetic field is proportional to its amplitude squared (E2 or B2).

The electric field describes an electromagnetic wave completely in free space. The magnetic field is related to the electric field by a simple relationship. Start from Faraday's law.

∇ x E= -dB/dt ……….(1)

From left side . Substitute the one dimensional wave equation for electricity and find its curl.

……….(2)

From right side, Substitute the one dimensional wave equation for magnetism and find its time derivative.

……….(3)

Set the two sides equal. Cancel the cosine terms and some other stuff. We will get

E0 = fB0 ……….(4)

After Rearranging it

= fλ ……….(5)

And we know that fλ is the speed of light. So the above equation can be written as

= c ……….(6)

This knowledge can then be used to simplify the energy density situation a bit. Start with the magnetic energy density and replace it with an expression containing the electric field.

……….(7)

Recall that the speed of light is related to the permeability and permittivity constants.

c = ……….(8)

= μ0ε0

Thus

ηB = μ0ε0 = ……….(9)

It's the electric energy density. For an electromagnetic wave in free space, half the energy is in the electric field and half is in the magnetic field

η = ηE + ηB

η = + ……….(10)

This gives us this compact equation for the total energy density of an electromagnetic wave.

η = ε0E2 ……….(11)

or this one, if you prefer to state things in terms of the magnetic field instead

η = B2 ……….(12)

This is an interesting and simple set of relations, but keeps in mind that it only works for electromagnetic waves in free space. Things are different in a media and the electric and magnetic fields can have any values they want if they're static (meaning there's no accelerating charges).

Since waves are spread out in space and time, energy density is often a more useful concept than energy.

Q9) A light bulb emits 5.00 W of power as visible light. What are the average electric and magnetic fields from the light at a distance of 3.0 m?A9)

Assume the bulb’s power output P is distributed uniformly over a sphere of radius 3.0 m to calculate the intensity, and from it, the electric field.

The power radiated as visible light is then

Q10) The beam from a small laboratory laser typically has an intensity of about 1.0 x 10-3 W/m2. Assuming that the beam is composed of plane waves; calculate the amplitudes of the electric and magnetic fields in the beam. A10)

The intensity of the laser beam is

I = c

The amplitude of electric field is therefore

=0.87 V/m

The amplitude of magnetic field can be obtained by

B0 = E0/ c

=2.9 x 10-9 T

Q11) Solar Constant At the upper surface of the Earth’s atmosphere, the time-averaged magnitude of the Poynting vector, <S> = 1.35x103 W/m2, is referred to as the solar constant.(a) Assuming that the Sun’s electromagnetic radiation is a plane sinusoidal wave, what are the magnitudes of the electric and magnetic fields? (b)What is the total time-averaged power radiated by the Sun? The mean Sun-Earth distance is R= 1.50x1011mA11)

(a)The time-averaged Poynting vector is related to the amplitude of the electric field by

<S> = =

The amplitude of electric field is therefore

The amplitude of magnetic field can be obtained by

B0 = E0/ c

= = 3.4 x 10-6 T

The associated magnetic field is one tenth of the earth’s magnetic field.

(b) The total time averaged power radiated by the Sun at the distance R is

<P> =<S>A =<S> 4πR2

=1.35x103 4 x 3.14 x (1.50x1011)2

= 3.8 x 1026 W

The type of wave discussed in the example above is a spherical wave, which originates from a “point-like” source. The intensity at a distance r from the source is which decreases is .

I =<S> = <P> /4πR2

Which decreases as 1/r2, On the other hand, the intensity of a plane wave remains constant and there is no spreading in its energy.

Q12) Assume the helium-neon lasers commonly used in student physics laboratories have power outputs of 0.250 mW.(a) If such a laser beam is projected onto a circular spot 1.00 mm in diameter, what is its intensity?(b) Find the peak magnetic field strength.(c) Find the peak electric field strength.A12)

Q13) What is the intensity of an electromagnetic wave with a peak electric field strength of 125 V/m?A13)

Q14) Let an electromagnetic wave propagate along the x direction, the magnetic field oscillates at a frequency of 1010 Hz and has an amplitude of 10−5T, acting along the y - direction. Then, compute the wavelength of the wave. Also write down the expression for electric field in this case.A14)

Q15) If the relative permeability and relative permittivity of the medium is 1.0 and 2.25, respectively. Find the speed of the electromagnetic wave in this medium.A15)

Sign Up