Unit-2
Compound interest and Annuities
Q1) What do you understand by the term “Amount”.
A1)
Amount- This is the sum of the principal and the interest at any time.
The rate of interest is denoted by ‘i’.
Let the principal is 100 rs. And the interest is 8 then we can say that the rate of interest is 8 percent per annum or we can write it as r = 8%
Suppose ‘P’ is the principal and ‘n’ is the time for which the principal is given and ‘r’ be the rate of interest per annum
‘I’ be the amount of interest
And ‘i’ be the rate of interest per unit
Then-

Here- i = r/100
We can calculate the amount as-
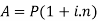
Q2) Rakhi invested 5000rs. At the rate of 8 per cent per annum then what will be the value of the amount she invested in 5 years.
A2)
Here P = 5000, i = 8/100 = 0.08, n = 5, now

Hence the required amount is - 7000
Q3) Find out the simple interest on 5600 rs. At 12 percent per annum from July 15 to September 26, 2020.
A3)
Here we calculate the time-
Total days from july 15 to sept 26 = 73 days or 73/365 = 1/5 years
And P = 5600, i = 12/100 = 0.12
Simple interest = P.i.n. = 5600 
Hence the simple interest is – 134.40
Q4) Harpreet invests 1200rs. At 10 percent per annum for some time and it becomes 1560 then find the principal when that will become 2232 at 8 percent p.a. in the same time.
A4)
Here in first situation- P = 1200, A = 1560 and i = 0.10
So that,




In second situation-
A = 2232, n = 3, i = 0.08



Q5) Define compound interest.
A5)
Compound interest-
In compound interest, the principal does not remain same but increases at the end of each interest period.
Let-
P- Principal
A - Amount
i = interest on re. 1 for a year
n = interest period
Then the amount can be calculated as-

And

Note- By using algorithm the above formula can be written as-

Q6) Aman invests 1000 rupees at 5 percent p.a for four years then find the compound interest on it.
A6)
Here P = 1000, i = 0.05 and n = 4
Then we know that-


On taking log, we get-
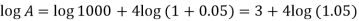


Compound interest will be-
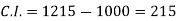
Which is the required answer.
Q7) A sum of money invested at C.I. payable yearly amounts to 10, 816 rs. at the end of the second year and to 11,248.64 rs. at the end of the third year. Find the rate of interest and the sum.
A7)
Here A1 = 10,816, n = 2, and A2 = 11,248.64, n = 3
We know that
A = P (1 + i)n we get,
10,816 =  … (i)
… (i)
11,248.64 = … (ii)
… (ii)
Here on dividing equation (2) by (1)-

We get-

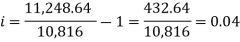
And

Hence the rate is 4 percent.
Now from first equation-
10,816 = 
Or

Now-
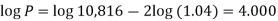
P = antilog 4.000 = 10,000
Therefore the require answer- 10,000
Q8) Define nominal and effective rate of interest.
A8)
Nominal rate of interest is the rate of interest per annum which is compounded yearly, half yearly, quarterly, monthly, n times in a year or continuously.
Effective rate of interest is the rate of interest per annum compounded only once in a year.
There is a relationships between nominal and effective rate of interest under two different conditions-



Where ‘r’ is nominal rate and ‘R’ is effective rate.
2. If compounding is continuous-

Or
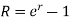
Q9) What is the relationship between nominal and effective rate.
A9)
If interest is compounded quarterly at  percent and the interest is compounded half yearly at
percent and the interest is compounded half yearly at  percent, then the relationship between the two is-
percent, then the relationship between the two is-



Q10) Ronak deposited Rs. 10,000 in a bank for 3 years. Bank gives two offers either 10 percent compounded quarterly or 8% compounded continuously, then which offer is preferable for Ronak?
A10)
Balance after three years under first offer-
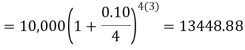
Balance after 3 years under second offer-

So that we can conclude that the first offer is preferable for Ronak.
Q11) What is present value.
A11)
Present value-
Present value of a given sum due at the end of a given period is that sum which together with its interest of the given period equals to the given sum.
Or in other words “Present value describes how much a future sum of money is worth today”.
Let the objective is to have an amount A after
n years from today. If the interest rate is ‘i’, then the amount is required to deposited now
so as to achieve the set target is-

Which is called the present value of A.
Note-

Q12) Find out the present value of Rs. 1000 due in 2 years at 5% per annum compound interest, If the interest is paid yearly.
A12)
Here, A = 1000, n = 2, i = 0.05
We have to find P-
By the formula-
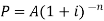



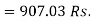
Therefore the present value is 
Q13) Find the present value of Rs. 4,500 due after 3 years from now. the interest is compounded continuously at the interest rate of 6%.
A13)
Here we have- A = 4500, t = 3, r = 0.06,
To find P,



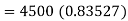

Q14) Give the formulas to find the amount of annuity.
A14)
The formulas to find the amount of annuity are given below-
| When annuity is payable annually and interest is also compounded annually |
| annuity is payable half-yearly and interest is also compounded half-yearly |
| annuity is payable quarterly and interest is also compounded quarterly |
Q15) Rajeev purchased a flat valued at 3,00,000rs. He paid 2,00,000 rs. at the time of purchase and agreed to pay the balance with interest of 12% per annum compounded half yearly in 20 equal half yearly installments.
If the first installment is paid after six months from the date of purchase, find the amount of each installment.
[Given log 10.6 = 1.0253 and log 31.19 = 1.494]
A15)
Here 2,00,000 has been paid at the time of purchase when cost of the flat was 3,00,000, we have to
consider 20 equated half yearly annuity payment P when 12% is rate of annual interest compounded half
yearly for present value of 1,00,000rs.
So that-

Or

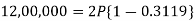

Then-

Hence the amount of each installment = 8,718.40
Suppose,

Taking log-
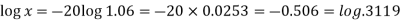
Hence
X = 0.3119
Q16) Rohan invests Rs. 5,000 in a term deposit plan. The plan offers an interest rate of 6% p.a., compounded quarterly. How much interest will John earn after one year? Also, what is the effective rate of interest?
A16)
Here we have-
P = 5000, i = 6% per annum or 0.06 p.a. or 0.015 per quarter
Compounding period = n = 4

Rohan earns Rs. 306.82 interest after a year
Now the effective rate of interest is-

Q17) A man buys a machine for Rs.20,00. What its value be after 6 years, if it is assumed to depreciate at a fixed rate of 12% per annum.
A17)
Here we have P = 20,000, n = 6 and r = -0.12 (rate of interest is negative in depreciation)
Then,

So that the value of the machine in 6 years will be = 9288.08
Q18) A machine valued at 500,000 depreciates at 6% per annum then in how many year its value will reduce to 100,000?
A18)
Here P = 500,000, r = 0.06, n = ? and the final value is = 100,000
We know that-

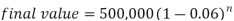



Taking log on both sides-

So that-

Therefore approximately it will take 26 years for the value decline to 100,000.
Q19) What do you understand by sinking funds.
A19)
Sinking funds-
A sinking fund is a special type of investment in which a constant amount is invested each year, usually with a view to reaching a specified value at a given point in the future. Questions need to be read carefully in order to be clear about exactly when the first and last installments are paid.


