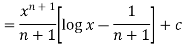Unit-3
Calculus
Q1) Differentiate the function f(x) =  by using the first principal method.
by using the first principal method.
A1)
We know that-

Here
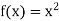
Substituting ( for x gives-
for x gives-

Hence-


Q2) Evaluate the 
A2)
We can simply find the Solutionution as follows,

Q3) Evaluate 
A3) 
Q4) Differentiate  with respect to x.
with respect to x.
A4)
Let 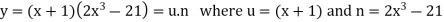


Now


Q5) if y =  then find dy/dx.
then find dy/dx.
A5)
Suppose z = 
Now-

So that-
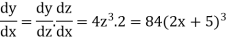
Q6) If y = log loglog then find dy/dx.
then find dy/dx.
A6)
Suppose y = log u where u = log v and v = log 



So that-

Q7) Find the derivative of 
A7)
Let y =  then-
then-


Q8) If y = log x/ x a then find 
A8)
First we will find the first derivative-

Now


Q9) if y = 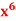 then find
then find  .
.
A9)
Here
y = 
Then


Q10) Calculate  and
and 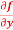 for the following function
for the following function
f(x , y) = 3x³-5y²+2xy-8x+4y-20
A10)
To calculate  treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
 =
=  [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
=  3x³] -
3x³] -  5y²] +
5y²] +  [2xy] -
[2xy] - 8x] +
8x] + 4y] -
4y] -  20]
20]
= 9x² - 0 + 2y – 8 + 0 – 0
= 9x² + 2y – 8
Similarly partial derivative of f(x,y) with respect to y is:
 =
= 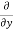 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 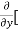 3x³] -
3x³] -  5y²] +
5y²] +  [2xy] -
[2xy] -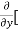 8x] +
8x] + 4y] -
4y] -  20]
20]
= 0 – 10y + 2x – 0 + 4 – 0
= 2x – 10y +4.
Q11) if 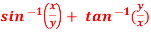 , then show that-
, then show that- 
A11)
Here we have,
u =  …………………..(1)
…………………..(1)
now partially differentiate eq.(1) w.r to x and y , we get

= 
Or
 ………………..(2)
………………..(2)
And now,

= 
 ………………….(3)
………………….(3)
Adding eq. (1) and (3) , we get
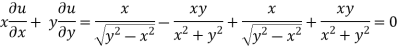
Hence proved.
Q12) If u = x²(y-x) + y²(x-y), then show that 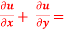 -2 (x – y)²
-2 (x – y)²
A12)
here, u = x²(y-x) + y²(x-y)
u = x²y - x³ + xy² - y³,
now differentiate u partially with respect to x and y respectively,
 = 2xy – 3x² + y² --------- (1)
= 2xy – 3x² + y² --------- (1)
 = x² + 2xy – 3y² ---------- (2)
= x² + 2xy – 3y² ---------- (2)
Now adding equation (1) and (2), we get
 = -2x² - 2y² + 4xy
= -2x² - 2y² + 4xy
= -2 (x² + y² - 2xy)
= -2 (x – y)²
Q13) State and prove Euler’s theorem.
A13)
Statement – if u = f(x, y) be a homogeneous function in x and y of degree n , then
x + y
+ y  = nu
= nu
Proof:
Here u is a homogeneous function of degree n,
u = xⁿ f(y/x) ----------------(1)
Partially differentiate equation (1) with respect to x,
 = n
= n f(y/x) + xⁿ f’(y/x).(
f(y/x) + xⁿ f’(y/x).( )
)
Now multiplying by x on both sides, we get
x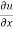 = n
= n f(y/x) + xⁿ f’(y/x).(
f(y/x) + xⁿ f’(y/x).( ) ---------- (2)
) ---------- (2)
Again partially differentiate equation (1) with respect to y,
 = xⁿ f’(y/x).
= xⁿ f’(y/x).
Now multiplying by y on both sides,
y  = xⁿ f’(y/x).
= xⁿ f’(y/x). ---------------(3)
---------------(3)
By adding equation (2) and (3),
x y
y  = n
= n f(y/x) + + xⁿ f’(y/x).(
f(y/x) + + xⁿ f’(y/x).( ) + xⁿ f’(y/x).
) + xⁿ f’(y/x).
x y
y  = n
= n f(y/x)
f(y/x)
Here u = f( x, y) is homogeneous function, then - u =  f(y/x)
f(y/x)
Put the value of u in equation (4),
x y
y  = nu
= nu
Which is the Euler’s theorem.
Q13) If u(x,y,z) = log( tan x + tan y + tan z) , then prove that ,

A13)
Here we have,
u(x,y,z) = log( tan x + tan y + tan z) ………………..(1)
diff. eq.(1) w.r.t. x , partially , we get
 ……………..(2)
……………..(2)
diff. eq.(1) w.r.t. y , partially , we get
 ………………(3)
………………(3)
diff. eq.(1) w.r.t. z , partially , we get
 ……………………(4)
……………………(4)
Now multiply eq. 2 , 3 , 4 by sin 2x , sin 2y , sin 2z respectively and adding , in order to get the final result,
We get,



So that,

Q14) let q = 4x + 3y and x = t³ + t² + 1 , y = t³ - t² - t
Then find  .
.
A14)
 . =
. = 
Where,
f1 =  , f2 =
, f2 = 
In this example f1 = 4 , f2 = 3
Also,
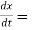 3t² + 2t ,
3t² + 2t , 
 4(3t² + 2t) + 3(
4(3t² + 2t) + 3(
= 21t² + 2t – 3
Q15) If u = u( y – z , z - x , x – y) then prove that  = 0
= 0
A15)
Let,

Then,
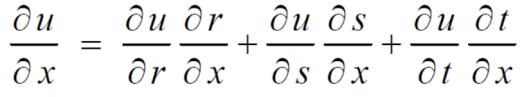

By adding all these equations we get,
 = 0
= 0
Hence proved.
Q16) If z is the function of x and y , and x =  , y =
, y =  , then prove that,
, then prove that,

A16)
Here , it is given that, z is the function of x and y & x , y are the functions of u and v.
So that,
 ……………….(1)
……………….(1)
And,
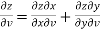 ………………..(2)
………………..(2)
Also there is,
x =  and y =
and y =  ,
,
now,
 ,
,  ,
,  ,
, 
From equation(1) , we get
 ……………….(3)
……………….(3)
And from eq. (2) , we get
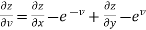 …………..(4)
…………..(4)
Subtracting eq. (4) from (3), we get
 =
= 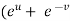 )
) – (
– (
= x
Hence proved.
Q17) Examine for maximum and minimum for the function f(x) = 
A17)
Here the first derivative is-


So that, we get-

Now we will get to know that the function is maximum or minimum at these values of x.
For x = 3
Let us assign to x, the values of 3 – h and 3 + h (here h is very small) and put these values at f(x).
Then-
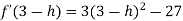 Which is negative for h is very small
Which is negative for h is very small
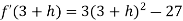 Which is positive
Which is positive
Thus f’(x) changes sign from negative to positive as it passes through x = 3.
So that f(x) is minimum at x = 3 and the minimum value is-
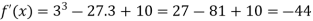
And f(x) is maximum at x = -3.
Q18) Find all points of maxima and minima of the function f(x) = .
.
A18)
Here,
f(x) = .
.
f’(x) =


Put, f’(x) = 0

We get,

Hence x = -1 and x = 3 are the critical values of the given function.
Now take,

Where x = -1, then f’’(x) = -12
Since f’’(x) < 0 at x = -1, the function has maxima at x = -1
And when x = 3, then f’’(x) = 12
Since f’’(x) > 12 at x = 3, the function has minima at x =
Q19) Find the integral of- 
A19)
We know that-

Then
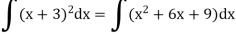


Q20) Evaluate the following integral-

A20)
Let us suppose,
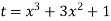
Then-
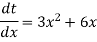
Or

Substituting –




Q21) Evaluate-

A21)
Here according to ILATE,
First function = log x
Second function = 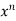
We know that-
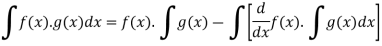
Then-


On solving, we get-