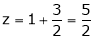UNIT 3
Question Bank
Question-1: evaluate 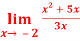
Sol.
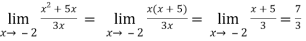
Question-2: Evaluate 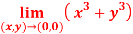
Sol . 1. 
2. 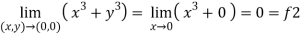
Here f1 = f2
3. Now put y = mx, we get
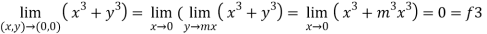
Here f1 = f2 = f3
Now put y = mx²
4. 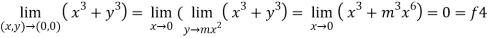
Therefore ,
F1 = f2 = f3 =f4
We can say that the limit exists with 0.
Question-3: : evaluate the following-
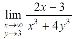
Sol. First we will calculate f1 –
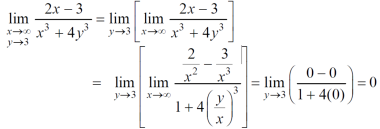
Here we see that f1 = 0
Now find f2,
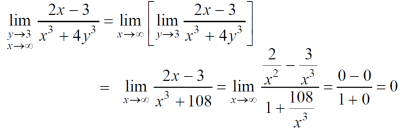
Here , f1 = f2
Therefore the limit exists with value 0.
Question-4: Calculate 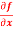 and
and 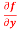 for the following function
for the following function
f(x , y) = 3x³-5y²+2xy-8x+4y-20
Sol. To calculate 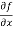 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
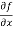 =
= 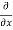 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 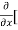 3x³] -
3x³] - 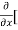 5y²] +
5y²] + 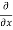 [2xy] -
[2xy] -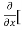 8x] +
8x] +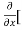 4y] -
4y] - 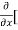 20]
20]
= 9x² - 0 + 2y – 8 + 0 – 0
= 9x² + 2y – 8
Similarly partial derivative of f(x,y) with respect to y is:
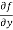 =
= 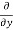 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 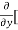 3x³] -
3x³] - 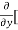 5y²] +
5y²] + 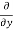 [2xy] -
[2xy] -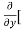 8x] +
8x] +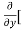 4y] -
4y] - 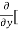 20]
20]
= 0 – 10y + 2x – 0 + 4 – 0
= 2x – 10y +4.
Question-5: if,
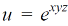
Then find.

Sol-
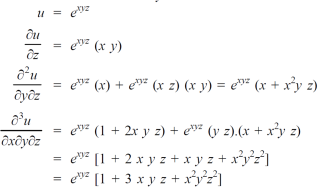
Question-6: if 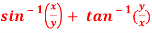 , then show that-
, then show that- 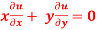
Sol. Here we have,
u = 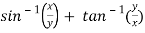 …………………..(1)
…………………..(1)
Now partially differentiate eq.(1) w.r to x and y , we get
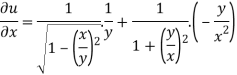
= 
Or
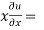
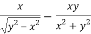 ………………..(2)
………………..(2)
And now,

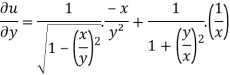
= 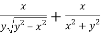
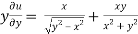 ………………….(3)
………………….(3)
Adding eq. (1) and (3) , we get

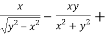
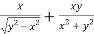 = 0
= 0
Hence proved.
Question-7: 3: if w = x² + y – z + sint and x + y = t, find
(a)  y,z
y,z
(b)  t, z
t, z
Sol. With x, y, z independent, we have
t = x + y, w = x² + y - z + sin (x + y).
Therefore,
 y,z = 2x + cos(x+y)
y,z = 2x + cos(x+y)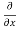 (x+y)
(x+y)
= 2x + cos (x + y)
With x, t, z independent, we have
Y = t-x, w= x² + (t-x) + sin t
thus 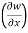 t, z = 2x – 1
t, z = 2x – 1
Question-8: If u = u( y – z , z - x , x – y) then prove that 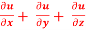 = 0
= 0
Sol. Let,
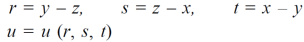
Then,
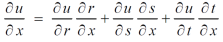

By adding all these equations we get,
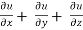 = 0 hence proved.
= 0 hence proved.
Question-9: If 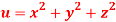 where
where  then find the value of
then find the value of 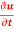 ?
?
Given 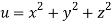
Where 
By chain rule
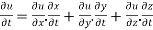
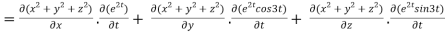

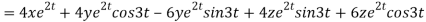
Now substituting the value of x ,y,z we get
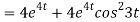 -6
-6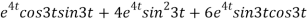
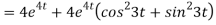
 8
8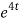
Question-10: If 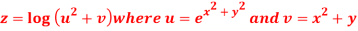 then calculate
then calculate 
Given 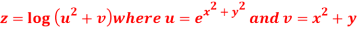
By Chain Rule
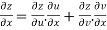
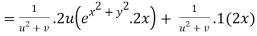
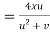
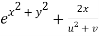
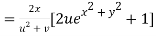
Putting the value of u = 
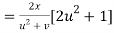
Again partially differentiating z with respect to y
By Chain Rule
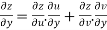
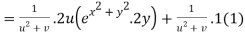
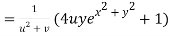
 by substituting value
by substituting value 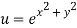
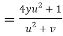
Question-11: : If u = u(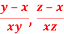 ), then prove that
), then prove that 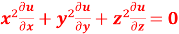 .
.
Sol. We are given that,
u = u (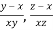 ) = u( r , s)
) = u( r , s)
Where r = 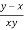 and s =
and s = 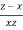
Or we can write as-
r = 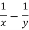 and s =
and s = 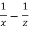
Differentiate them partially with respect to x , y and z. , we get
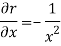

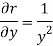

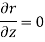

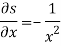

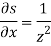


As we know that-

Then,

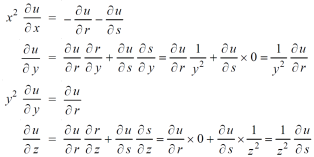
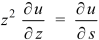
Adding all these results, we get
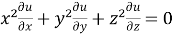 .
.
Question-12: If u = x + y + z , uv = y + z , uvw = z , find 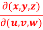
Sol. Here we have,
x = u – uv = u(1-v)
y = uv – uvw = uv( 1- w)
And z = uvw
So that,
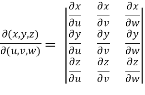
 =
=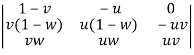
Apply 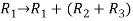
=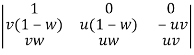
Now we get,
= u²v(1-w) + u²vw
= u²v
Question-13: Find the value of n so that the equation

Satisfies the relation 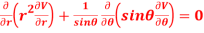
Given 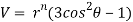
Partially differentiating V with respect to r keeping  as constant
as constant

Again partially differentiating given V with respect to 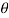 keeping r as constant
keeping r as constant
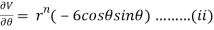
Now, we are taking the given relation
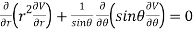
Substituting values using eq(i) and eq(ii)
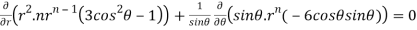

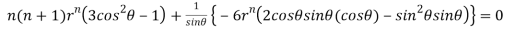
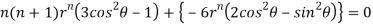
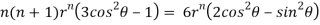
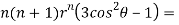
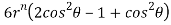
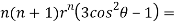
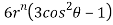

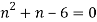
On solving we get 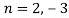
Question-14: If 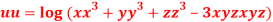
Then show that 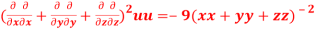
Given 
Partially differentiating u with respect to x keeping y and z as constant
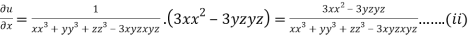
Similarly partially differentiating u with respect to y keeping x and z as constant
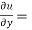
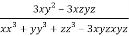 …….(ii)
…….(ii)
Similarly partially differentiating u with respect to z keeping x and y as constant
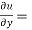
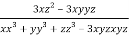 …….(iii)
…….(iii)
LHS: 
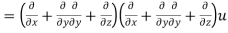

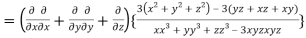
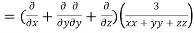
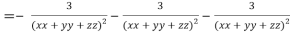
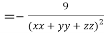
Hence proved
Question-15: Expand f(x , y) = 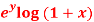 in powers of x and y about origin.
in powers of x and y about origin.
Sol. Here we have the function-
f(x , y) = 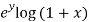
Here , a = 0 and b = 0 then
f(0 , 0) = 
Now we will find partial derivatives of the function-


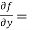
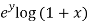
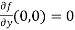
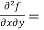

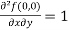
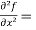
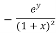
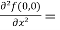
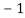

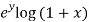


Now using Taylor’s theorem-
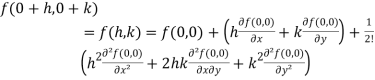 +………
+………
Suppose h = x and k = y , we get
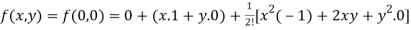 +…….
+…….
= 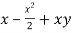 +……….
+……….
Question-16: Find the Taylor’s expansion of  about (1 , 1) up to second degree term.
about (1 , 1) up to second degree term.
Sol. We have,
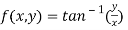
At (1 , 1)

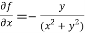
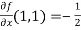

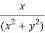
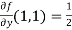
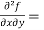
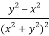
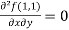
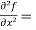

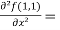


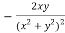
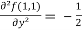
Now by using Taylor’s theorem-
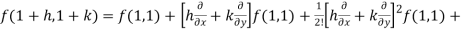 ……
……
Suppose 1 + h = x then h = x – 1
1 + k = y then k = y - 1
 ……
……
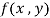 =
= 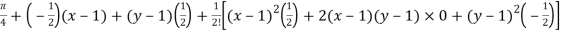
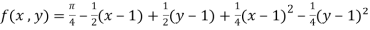 ……..
……..
Question-17: Find the maximum and minimum point of the function

Partially differentiating given equation with respect to and x and y then equate them to zero
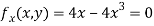
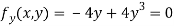
On solving above we get 
Also 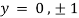
Thus we get the pair of values (0,0), (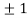 ,0) and (0,
,0) and (0,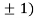
Now, we calculate
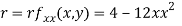
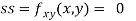
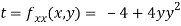
At the point (0,0)
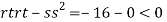
So function has saddle point at (0,0).
At the point (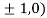
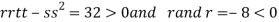
So the function has maxima at this point (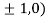 .
.
At the point (0,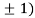
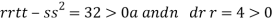
So the function has minima at this point (0,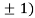 .
.
At the point (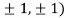
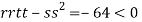
So the function has an saddle point at (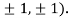
Question-18: Find the point on plane 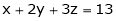 nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
Solution:
Let 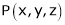 be the point on sphere
be the point on sphere  which is nearest to the point
which is nearest to the point 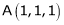 . Then shortest distance.
. Then shortest distance.
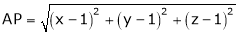
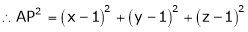
 Let
Let 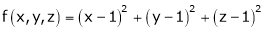
Under the condition 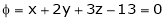 … (1)
… (1)
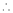 By method of Lagrange’s undetermined multipliers we have
By method of Lagrange’s undetermined multipliers we have

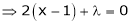 … (2)
… (2)
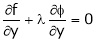
 … (3)
… (3)
i.e. 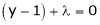 &
&
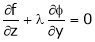
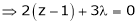 … (4)
… (4)
From (2) we get 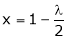
From (3) we get 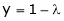
From (4) we get 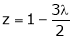
 Equation (1) becomes
Equation (1) becomes
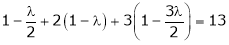
i.e. 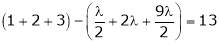

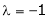
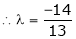
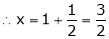
y = 2