UNIT 3

1. Explain Linear Search with examples

Linear search is the simplest search algorithm and often called sequential search. In this type of searching, we simply traverse the list completely and match each element of the list with the item whose location is to be found. If the match found then location of the item is returned otherwise the algorithm return NULL.

Linear search is mostly used to search an unordered list in which the items are not sorted. The algorithm of linear search is given as follows.

Algorithm

• LINEAR_SEARCH(A, N, VAL)
• Step 1: [INITIALIZE] SET POS = -1
• Step 2: [INITIALIZE] SET I = 1
• Step 3: Repeat Step 4 while I<=N
• Step 4: IF A[I] = VAL
  SET POS = I
  PRINT POS
  Go to Step 6
  [END OF IF]
  SET I = I + 1
  [END OF LOOP]
• Step 5: IF POS = -1
  PRINT " VALUE IS NOT PRESENTIN THE ARRAY "
  [END OF IF]
• Step 6: EXIT

Complexity of algorithm

C Program

1. #include<stdio.h>   
2. Void main ()  
3. {  
4.    Int a[10] = {10, 23, 40, 1, 2, 0, 14, 13, 50, 9};  
5.    Int item, i,flag;  
6.    Printf("\nEnter Item which is to be searched\n");  
7.    Scanf("%d",&item);  
8.    For (i = 0; i< 10; i++)  
9.    {  
10.        If(a[i] == item)   
11.        {  
12.            Flag = i+1;  
13.            Break;  
14.        }   
15.        Else   
16.        Flag = 0;  
17.    }   
18.    If(flag != 0)  
19.    {  
20.        Printf("\nItem found at location %d\n",flag);  
21.    }  
22.    Else  
23.    {  
24.        Printf("\nItem not found\n");   
25.    }  
26. }   

Output:

Enter Item which is to be searched

20

Item not found

Enter Item which is to be searched

23

Item found at location 2

2.     Explain Binary Search with examples

Binary search is the search technique which works efficiently on the sorted lists. Hence, in order to search an element into some list by using binary search technique, we must ensure that the list is sorted.

Binary search follows divide and conquer approach in which, the list is divided into two halves and the item is compared with the middle element of the list. If the match is found then, the location of middle element is returned otherwise, we search into either of the halves depending upon the result produced through the match.

Binary search algorithm is given below.

BINARY_SEARCH(A, lower_bound, upper_bound, VAL)

• Step 1: [INITIALIZE] SET BEG = lower_bound
  END = upper_bound, POS = - 1
• Step 2: Repeat Steps 3 and 4 while BEG <=END
• Step 3: SET MID = (BEG + END)/2
• Step 4: IF A[MID] = VAL
  SET POS = MID
  PRINT POS
  Go to Step 6
  ELSE IF A[MID] > VAL
  SET END = MID - 1
  ELSE
  SET BEG = MID + 1
  [END OF IF]
  [END OF LOOP]
• Step 5: IF POS = -1
  PRINT "VALUE IS NOT PRESENT IN THE ARRAY"
  [END OF IF]
• Step 6: EXIT

Complexity

Example

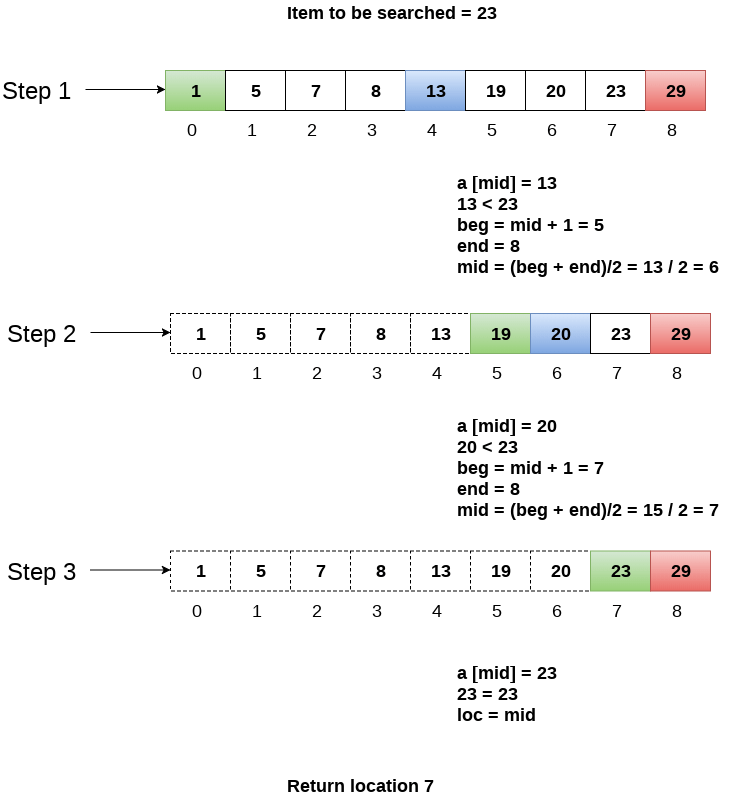
Let us consider an array arr = {1, 5, 7, 8, 13, 19, 20, 23, 29}. Find the location of the item 23 in the array.

In 1st step :

1. BEG = 0   
2. END = 8ron  
3. MID = 4   
4. a[mid] = a[4] = 13 < 23, therefore  

In Second step:

1. Beg = mid +1 = 5   
2. End = 8  
3. Mid = 13/2 = 6    
4. a[mid] = a[6] = 20 < 23, therefore;   

In third step:

1. Beg = mid + 1 = 7   
2. End = 8   
3. Mid = 15/2 = 7  
4. a[mid] = a[7]   
5. a[7] = 23 = item;   
6. Therefore, set location = mid;   
7. The location of the item will be 7.   

Binary Search Program using Recursion

C program

1. #include<stdio.h>  
2. Int binarySearch(int[], int, int, int);  
3. Void main ()  
4. {  
5.    Int arr[10] = {16, 19, 20, 23, 45, 56, 78, 90, 96, 100};  
6.    Int item, location=-1;   
7.    Printf("Enter the item which you want to search ");  
8.    Scanf("%d",&item);  
9.    Location = binarySearch(arr, 0, 9, item);  
10.    If(location != -1)   
11.    {  
12.        Printf("Item found at location %d",location);  
13.    }  
14.    Else  
15.    {  
16.        Printf("Item not found");  
17.    }  
18. }   
19. Int binarySearch(int a[], int beg, int end, int item)  
20. {  
21.    Int mid;  
22.    If(end >= beg)   
23.    {     
24.        Mid = (beg + end)/2;  
25.        If(a[mid] == item)  
26.        {  
27.            Return mid+1;  
28.        }  
29.        Else if(a[mid] < item)   
30.        {  
31.            Return binarySearch(a,mid+1,end,item);  
32.        }  
33.        Else   
34.        {  
35.            Return binarySearch(a,beg,mid-1,item);  
36.        }  
37.      
38.    }  
39.    Return -1;   
40. }  

Output:

Enter the item which you want to search

19

Item found at location 2

3.     Explain Bubble Sort with examples

In Bubble sort, Each element of the array is compared with its adjacent element. The algorithm processes the list in passes. A list with n elements requires n-1 passes for sorting. Consider an array A of n elements whose elements are to be sorted by using Bubble sort. The algorithm processes like following.

1. In Pass 1, A[0] is compared with A[1], A[1] is compared with A[2], A[2] is compared with A[3] and so on. At the end of pass 1, the largest element of the list is placed at the highest index of the list.
2. In Pass 2, A[0] is compared with A[1], A[1] is compared with A[2] and so on. At the end of Pass 2 the second largest element of the list is placed at the second highest index of the list.
3. In pass n-1, A[0] is compared with A[1], A[1] is compared with A[2] and so on. At the end of this pass. The smallest element of the list is placed at the first index of the list.

Algorithm :

• Step 1: Repeat Step 2 For i = 0 to N-1
• Step 2: Repeat For J = i + 1 to N - I
• Step 3: IF A[J] > A[i]
  SWAP A[J] and A[i]
  [END OF INNER LOOP]
  [END OF OUTER LOOP
• Step 4: EXIT

Complexity

C Program

1. #include<stdio.h>  
2. Void main ()  
3. {  
4.    Int i, j,temp;   
5.    Int a[10] = { 10, 9, 7, 101, 23, 44, 12, 78, 34, 23};   
6.    For(i = 0; i<10; i++)  
7.    {  
8.        For(j = i+1; j<10; j++)  
9.        {  
10.            If(a[j] > a[i])  
11.            {  
12.                Temp = a[i];  
13.                a[i] = a[j];  
14.                a[j] = temp;   
15.            }   
16.        }   
17.    }   
18.    Printf("Printing Sorted Element List ...\n");  
19.    For(i = 0; i<10; i++)  
20.    {  
21.        Printf("%d\n",a[i]);  
22.    }  
23. }  

Output:

Printing Sorted Element List . . .

7

9

10

12

23

34

34

44

78

101

C++ Program

1. #include<iostream>  
2. Using namespace std;  
3. Int main ()  
4. {  
5.    Int i, j,temp;   
6.    Int a[10] = { 10, 9, 7, 101, 23, 44, 12, 78, 34, 23};   
7.    For(i = 0; i<10; i++)  
8.    {  
9.        For(j = i+1; j<10; j++)  
10.        {  
11.            If(a[j] < a[i])  
12.            {  
13.                Temp = a[i];  
14.                a[i] = a[j];  
15.                a[j] = temp;   
16.            }   
17.        }   
18.    }   
19.    Cout <<"Printing Sorted Element List ...\n";  
20.    For(i = 0; i<10; i++)  
21.    {  
22.        Cout <<a[i]<<"\n";  
23.    }  
24.    Return 0;  
25. }  

Output:

Printing Sorted Element List ...

7

9

10

12

23

23

34

44

78

101

4.     Explain Selection Sort with examples

Selection sort is a simple sorting algorithm. This sorting algorithm is an in-place comparison-based algorithm in which the list is divided into two parts, the sorted part at the left end and the unsorted part at the right end. Initially, the sorted part is empty and the unsorted part is the entire list.

The smallest element is selected from the unsorted array and swapped with the leftmost element, and that element becomes a part of the sorted array. This process continues moving unsorted array boundary by one element to the right.

This algorithm is not suitable for large data sets as its average and worst case complexities are of Ο(n2), where n is the number of items.

How Selection Sort Works?

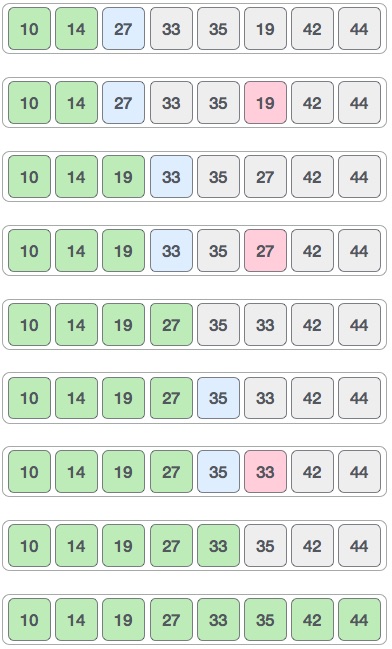
Consider the following depicted array as an example.

For the first position in the sorted list, the whole list is scanned sequentially. The first position where 14 is stored presently, we search the whole list and find that 10 is the lowest value.

So we replace 14 with 10. After one iteration 10, which happens to be the minimum value in the list, appears in the first position of the sorted list.

For the second position, where 33 is residing, we start scanning the rest of the list in a linear manner.

We find that 14 is the second lowest value in the list and it should appear at the second place. We swap these values.

After two iterations, two least values are positioned at the beginning in a sorted manner.

The same process is applied to the rest of the items in the array.

Following is a pictorial depiction of the entire sorting process −

Now, let us learn some programming aspects of selection sort.

Algorithm

Step 1 − Set MIN to location 0

Step 2 − Search the minimum element in the list

Step 3 − Swap with value at location MIN

Step 4 − Increment MIN to point to next element

Step 5 − Repeat until list is sorted

Pseudocode

Procedure selection sort

   list  : array of items

   n     : size of list

   for i = 1 to n - 1

   /* set current element as minimum*/

      min = i   

      /* check the element to be minimum */

      for j = i+1 to n

         if list[j] < list[min] then

            min = j;

         end if

      end for

      /* swap the minimum element with the current element*/

      if indexMin != i  then

         swap list[min] and list[i]

      end if

   end for

End procedure

5.     Give an example of selection sort

Selection sort is a simple sorting algorithm. This sorting algorithm is an in-place comparison-based algorithm in which the list is divided into two parts, the sorted part at the left end and the unsorted part at the right end. Initially, the sorted part is empty and the unsorted part is the entire list.

Implementation in C

#include <stdio.h>

#include <stdbool.h>

#define MAX 7

Int intArray[MAX] = {4,6,3,2,1,9,7};

Void printline(int count) {

   int i;

   for(i = 0;i < count-1;i++) {

      printf("=");

   }

   printf("=\n");

}

Void display() {

   int i;

   printf("[");

   // navigate through all items

   for(i = 0;i < MAX;i++) {

      printf("%d ", intArray[i]);

   }

   printf("]\n");

}

Void selectionSort() {

   int indexMin,i,j;

   // loop through all numbers

   for(i = 0; i < MAX-1; i++) {

      // set current element as minimum

      indexMin = i;

      // check the element to be minimum

      for(j = i+1;j < MAX;j++) {

         if(intArray[j] < intArray[indexMin]) {

            indexMin = j;

         }

      }

      if(indexMin != i) {

         printf("Items swapped: [ %d, %d ]\n" , intArray[i], intArray[indexMin]);

         // swap the numbers

         int temp = intArray[indexMin];

         intArray[indexMin] = intArray[i];

         intArray[i] = temp;

      }         

      printf("Iteration %d#:",(i+1));

      display();

   }

} 

Void main() {

   printf("Input Array: ");

   display();

   printline(50);

   selectionSort();

   printf("Output Array: ");

   display();

   printline(50);

}

If we compile and run the above program, it will produce the following result −

Output

Input Array: [4 6 3 2 1 9 7 ]

==================================================

Items swapped: [ 4, 1 ]

Iteration 1#:[1 6 3 2 4 9 7 ]

Items swapped: [ 6, 2 ]

Iteration 2#:[1 2 3 6 4 9 7 ]

Iteration 3#:[1 2 3 6 4 9 7 ]

Items swapped: [ 6, 4 ]

Iteration 4#:[1 2 3 4 6 9 7 ]

Iteration 5#:[1 2 3 4 6 9 7 ]

Items swapped: [ 9, 7 ]

Iteration 6#:[1 2 3 4 6 7 9 ]

Output Array: [1 2 3 4 6 7 9 ]

==================================================

6.     Write a program for Finding roots of Equations

The standard form of a quadratic equation is:

Ax2 + bx + c = 0, where

a, b and c are real numbers and

a != 0

The term b2-4ac is known as the discriminant of a quadratic equation. It tells the nature of the roots.

• If the discriminant is greater than 0, the roots are real and different.
• If the discriminant is equal to 0, the roots are real and equal.
• If the discriminant is less than 0, the roots are complex and different.

Program to Find Roots of a Quadratic Equation

#include <math.h>

#include <stdio.h>

Int main() {

    double a, b, c, discriminant, root1, root2, realPart, imagPart;

    printf("Enter coefficients a, b and c: ");

    scanf("%lf %lf %lf", &a, &b, &c);

    discriminant = b * b - 4 * a * c;

    // condition for real and different roots

    if (discriminant > 0) {

        root1 = (-b + sqrt(discriminant)) / (2 * a);

        root2 = (-b - sqrt(discriminant)) / (2 * a);

        printf("root1 = %.2lf and root2 = %.2lf", root1, root2);

    }

    // condition for real and equal roots

    else if (discriminant == 0) {

        root1 = root2 = -b / (2 * a);

        printf("root1 = root2 = %.2lf;", root1);

    }

    // if roots are not real

    else {

        realPart = -b / (2 * a);

        imagPart = sqrt(-discriminant) / (2 * a);

        printf("root1 = %.2lf+%.2lfi and root2 = %.2f-%.2fi", realPart, imagPart, realPart, imagPart);

    }

    return 0;

}

Output

Enter coefficients a, b and c: 2.3

4

5.6

Root1 = -0.87+1.30i and root2 = -0.87-1.30i

In this program, the sqrt() library function is used to find the square root of a number.

7.     What are functions explain in detail with examples?

In c, we can divide a large program into the basic building blocks known as function. The function contains the set of programming statements enclosed by {}. A function can be called multiple times to provide reusability and modularity to the C program. In other words, we can say that the collection of functions creates a program. The function is also known as procedureor subroutinein other programming languages.

Advantage of functions in C

There are the following advantages of C functions.

• By using functions, we can avoid rewriting same logic/code again and again in a program.
• We can call C functions any number of times in a program and from any place in a program.
• We can track a large C program easily when it is divided into multiple functions.
• Reusability is the main achievement of C functions.
• However, Function calling is always a overhead in a C program.

Function Aspects

There are three aspects of a C function.

• Function declaration A function must be declared globally in a c program to tell the compiler about the function name, function parameters, and return type.

• Function call Function can be called from anywhere in the program. The parameter list must not differ in function calling and function declaration. We must pass the same number of functions as it is declared in the function declaration.

• Function definition It contains the actual statements which are to be executed. It is the most important aspect to which the control comes when the function is called. Here, we must notice that only one value can be returned from the function.

The syntax of creating function in c language is given below:

1. Return_type function_name(data_type parameter...){  
2. //code to be executed  
3. }  

Types of Functions

There are two types of functions in C programming:

1. Library Functions: are the functions which are declared in the C header files such as scanf(), printf(), gets(), puts(), ceil(), floor() etc.
2. User-defined functions: are the functions which are created by the C programmer, so that he/she can use it many times. It reduces the complexity of a big program and optimizes the code.

Return Value

A C function may or may not return a value from the function. If you don't have to return any value from the function, use void for the return type.

Let's see a simple example of C function that doesn't return any value from the function.

Example without return value:

1. Void hello(){  
2. Printf("hello c");  
3. }  

If you want to return any value from the function, you need to use any data type such as int, long, char, etc. The return type depends on the value to be returned from the function.

Let's see a simple example of C function that returns int value from the function.

Example with return value:

1. Int get(){  
2. Return 10;  
3. }  

In the above example, we have to return 10 as a value, so the return type is int. If you want to return floating-point value (e.g., 10.2, 3.1, 54.5, etc), you need to use float as the return type of the method.

1. Float get(){  
2. Return 10.2;  
3. }  

Now, you need to call the function, to get the value of the function.

Different aspects of function calling

A function may or may not accept any argument. It may or may not return any value. Based on these facts, There are four different aspects of function calls.

• Function without arguments and without return value
• Function without arguments and with return value
• Function with arguments and without return value
• Function with arguments and with return value

8.     Example for Function without argument and return value

Example 1

1. #include<stdio.h>  
2. Void printName();  
3. Void main ()  
4. {  
5.    Printf("Hello ");  
6.    PrintName();  
7. }  
8. Void printName()  
9. {  
10.    Printf("Javatpoint");  
11. }  

Output

Hello Javatpoint

Example 2

1. #include<stdio.h>  
2. Void sum();  
3. Void main()  
4. {  
5.    Printf("\nGoing to calculate the sum of two numbers:");  
6.    Sum();  
7. }  
8. Void sum()  
9. {  
10.    Int a,b;   
11.    Printf("\nEnter two numbers");  
12.    Scanf("%d %d",&a,&b);   
13.    Printf("The sum is %d",a+b);  
14. }  

Output

Going to calculate the sum of two numbers:

Enter two numbers 10

24

The sum is 34

9.     Example for Function with argument and with return value

Example 1

1. #include<stdio.h>  
2. Int sum(int, int);  
3. Void main()  
4. {  
5.    Int a,b,result;   
6.    Printf("\nGoing to calculate the sum of two numbers:");  
7.    Printf("\nEnter two numbers:");  
8.    Scanf("%d %d",&a,&b);  
9.    Result = sum(a,b);  
10.    Printf("\nThe sum is : %d",result);  
11. }  
12. Int sum(int a, int b)  
13. {  
14.    Return a+b;  
15. }  

Output

Going to calculate the sum of two numbers:

Enter two numbers:10

20

The sum is : 30  

Example 2: Program to check whether a number is even or odd

1. #include<stdio.h>  
2. Int even_odd(int);  
3. Void main()  
4. {  
5. Int n,flag=0;  
6. Printf("\nGoing to check whether a number is even or odd");  
7. Printf("\nEnter the number: ");  
8. Scanf("%d",&n);  
9. Flag = even_odd(n);  
10. If(flag == 0)  
11. {  
12.    Printf("\nThe number is odd");  
13. }  
14. Else   
15. {  
16.    Printf("\nThe number is even");  
17. }  
18. }  
19. Int even_odd(int n)  
20. {  
21.    If(n%2 == 0)  
22.    {  
23.        Return 1;  
24.    }  
25.    Else   
26.    {  
27.        Return 0;  
28.    }  
29. }  

Output

Going to check whether a number is even or odd

Enter the number: 100

The number is even

10. What is Library Functions?

Library functions are the inbuilt function in C that are grouped and placed at a common place called the library. Such functions are used to perform some specific operations. For example, printf is a library function used to print on the console. The library functions are created by the designers of compilers. All C standard library functions are defined inside the different header files saved with the extension .h. We need to include these header files in our program to make use of the library functions defined in such header files. For example, To use the library functions such as printf/scanf we need to include stdio.h in our program which is a header file that contains all the library functions regarding standard input/output.

The list of mostly used header files is given in the following table.