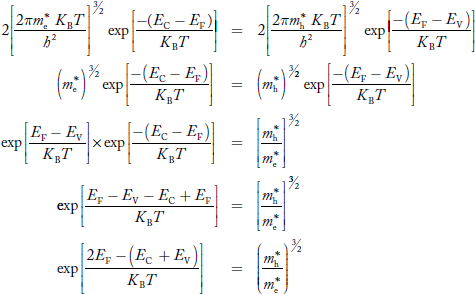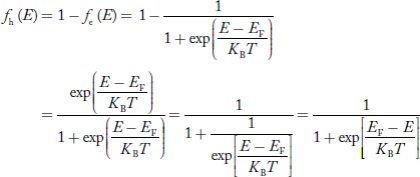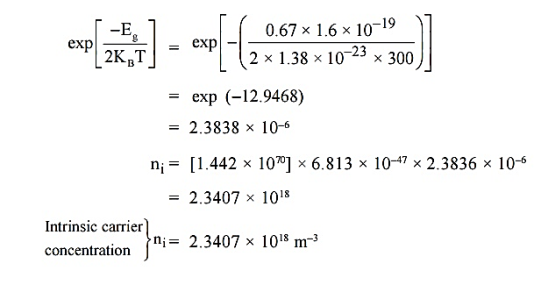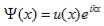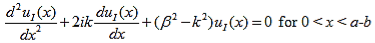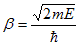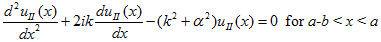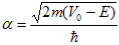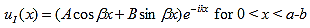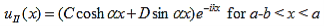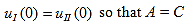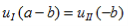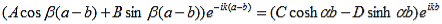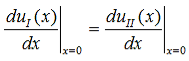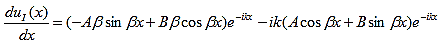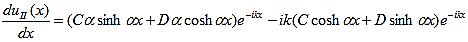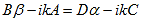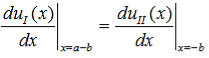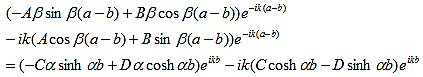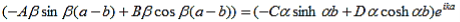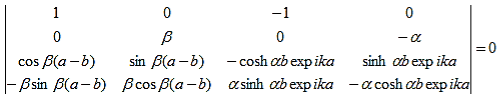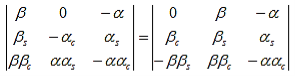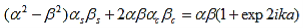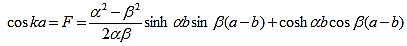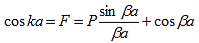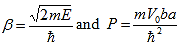|
|
|
Taking logarithms on both sides, we get
|
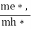 is very small so that EF is just lie in the middle of energy gap Temperature effect on Fermi levelFermi level slightly rises with increase of temperature.But in case of pure intrinsic semiconductor like Si and Ge, mh* ≈ me* so in these cases Fermi level lies at the middle of energy gap. Q5) Derive expression for carrier concentration for intrinsic semiconductors? A 5)Intrinsic semiconductors—carrier concentrationHere we will calculate the number of electrons excited into conduction band at temperature T and also the hole concentration in the valence band. It is assumed that the electrons in the conduction band behave as if they are free particles with effective mass me* and the holes near the top of the valence band behave as if they are free particles with effective mass mh*. Here we will calculate the electron concentration, hole concentrationDensity of Electrons in Conduction Band
is very small so that EF is just lie in the middle of energy gap Temperature effect on Fermi levelFermi level slightly rises with increase of temperature.But in case of pure intrinsic semiconductor like Si and Ge, mh* ≈ me* so in these cases Fermi level lies at the middle of energy gap. Q5) Derive expression for carrier concentration for intrinsic semiconductors? A 5)Intrinsic semiconductors—carrier concentrationHere we will calculate the number of electrons excited into conduction band at temperature T and also the hole concentration in the valence band. It is assumed that the electrons in the conduction band behave as if they are free particles with effective mass me* and the holes near the top of the valence band behave as if they are free particles with effective mass mh*. Here we will calculate the electron concentration, hole concentrationDensity of Electrons in Conduction BandThe number of free electrons per unit volume of semiconductor having energies in between E and E + dE is represented as N(E) dE dE = width of Energy band Therefore, we have: N(E) dE = ge(E) dE fe(E) ……….(1) ge(E) = The density of electron states per unit volume fe(E) = Fermi-Dirac distribution function i.e. probability that an electron occupies an electron state The number of electrons present in the conduction band per unit volume of material ‘n’ is obtained by integrating N(E) dE between the limits Ec and Ect Where Ec = the bottom energy levels of conduction band Ect = the bottom and top energy levels of conduction band n = can be written as n = n = we know that above Ect, there is no electrons. Hence, Equation (3) becomes n = n = The Fermi-Dirac distribution function fe(E) can be represented as:
Compared to the exponential value, so the ‘1’ in the denominator can be neglected. So Hence, The density of electron states ge(E) in the energy space from E = 0 to E can be written as:
where me* is the effective mass of an electron and h is Planck’s constant.
To evaluate n, the density of states is counted from Ec, since the minimum energy state in conduction band is Ec. so eq (8) can become
Substituting Equations (6) and (9) in (4) gives n = n = The above equation can be simplified by the following substitution: Put ɛ = E − Ec ………… (11) So, dɛ = dE In Equation (11), Ec is constant, as we change the variable E to ε in Equation (10), the integral limits also change. In Equation (11), as E → Ec then ε → 0 and E → ∞, then ε also → ∞. the exponential term in Equation (10) becomes:
Substituting Equations (11) and (12) in (10), we get: n = n = Above integral (I) can be simplified by substitution. Put ε = x2 so that dɛ = 2x dx I = = = Substituting Equation (14) in (13) gives: n = n = n = n = The term n =Nc Density of Holes in Valence Band The number of holes per unit volume of semiconductor in the energy range E and E + dE in valence band is represented as P(E) dE. Proceeding same way( as in case of electrons) we have Therefore, we have: P(E) dE = gh(E) dE fh(E) ……….(17) dE = width of Energy band gh(E) = The density of holes states per unit volume fh(E) = Fermi-Dirac distribution function i.e. probability that an hole occupies an electron state The number of electrons present in the conduction band per unit volume of material ‘n’ is obtained by integrating P(E) dE between the limits Evb and EV where EV = the bottom energy levels of valence band Evb = the bottom and top energy levels of valence band The total number of holes present in the valence band per unit volume of material ‘p’ is obtained by integrating P(E) dE
Equation (18) can be represented as:
Now we know that below Evb no holes is present. Hence, Equation (19) becomes
We know hole can also be defined as absence of an electron. presence of a hole = the absence of an electron Hence, the Fermi-Dirac function of holes fh(E) in the valence band is:
Compared to exponential, the ‘1’ in the denominator is negligible, Hence,
The density of hole states between E and E + dE in valence band can be written similar to Equation (8.9) for electrons.
Where mh* is the effective mass of hole. Substituting Equations (21) and (22) in (20),
The above equation can be simplified by the substitution: Put ɛ = EV − E ............. (24) so dɛ = − dE In Equation (24), EV is constant, as we change the variable E to ε in Equation (23), the integral limits also change. In Equation (24), as E → EV then ε → 0 and E→ −∞, then ε → ∞ the exponential term in Equation (23) becomes:
Substituting Equations (24) and (25) in (23), we get:
From Equation (14), we know the integral value
….The term
|
|
At equilibrium, the Lorentz force on a carrier FL = Bevd ……………..(1) and the Hall force FH = eEH ……………..(2) Where EH is the Hall electric field due to accumulated charge. At equilibrium, FH = FL eEH = Bevd ∴ EH = Bvd ……………..(3) If ‘d’ is the distance between the upper and lower surfaces of the slab, then the Hall field EH = In n-type material, Jx = –nevd vd = - Where n is free electron concentration, substituting (5) in (3), we have ∴ EH = -B For a given semiconductor, the Hall field EH is proportional to the current density Jx and the intensity of magnetic field ‘B’ in the material. i.e. EH ∝ JxB (or) EH = RHJxB ……………..(7) Where RH = Hall coefficient Equations (6) and (7) are the same so, we have RHJxB =-B RH = - Where ρ is the charge density Similarly for p-type material RH = Using Equations (8) and (9), carrier concentration can be determined. Thus, the Hall coefficient is negative for n-type material. In n-type material, as the more negative charge is deposited at the bottom surface, so the top face acquires positive polarity and the Hall field is along negative Y-direction. The polarity at the top and bottom faces can be measured by applying probes. Similarly, in the case of p-type material, a more positive charge is deposited at the bottom surface. So, the top face acquires negative polarity and the Hall field is along positive Y-direction. Thus, the sign of the Hall coefficient decides the nature of (n-type or p-type) material. The Hall coefficient can be determined experimentally in the following way: Multiplying Equation (7) with ‘d’, we have EHd = VH = RHJxBd ……………..(10) From (Figure 15) we know the current density Jx Jx = Where W is the width of the box. Then, Equation (10) becomes VH = RH RH = Substituting the measured values of VH, Ix, B, and W in Equation(11), RH is obtained. The polarity of VH will be the opposite for n- and p-type semiconductors. The mobility of charge carriers can be found by using the Hall effect, for example, the conductivity of electrons is n = neμn Or we can rewrite it as μn = by using equation (11) μn = n
|
- For N-type, Hall coefficient RH= negative
- For P-type, Hall coefficient RH= Positive
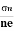 =n RH. Where 𝜎= electrical conductivity
=n RH. Where 𝜎= electrical conductivity
|
|
|
|
|
|
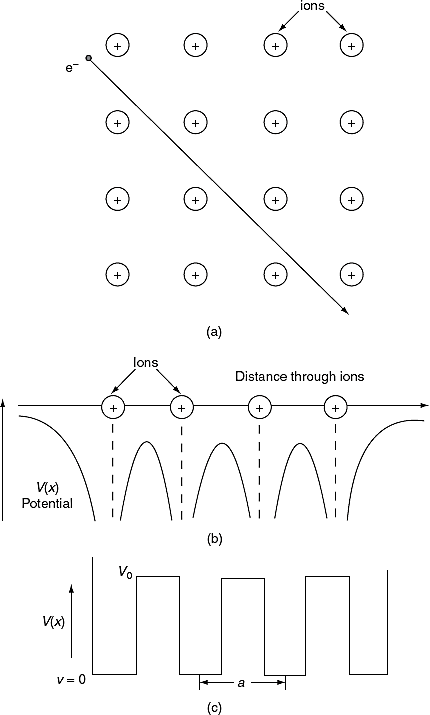
The solution to Schrödinger's equation for the Kronig-Penney potential is obtained by assuming that the solution is a Bloch function, namely a traveling wave solution of the form, eikx, multiplied with a periodic solution, u(x), which has the same periodicity as the periodic potential . The total wave function is therefore of the form:
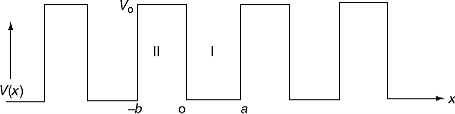
where u(x) is the periodic function as defined by u(x) = u(x + a), and k(x) is the wave number. We now rewrite Schrödinger equation using this wave function considering first region I, between the barriers where V(x) = 0 and then region II, the barrier region where V(x) = V0: In region I, Schrödinger's equation becomes:
with
Since the potential, V(x), is finite everywhere, the solutions for uI(x) and uII(x) must be continuous as well as their first derivatives. Continuity at x = 0 results in:
and continuity at x = a-b combined with the requirement that u(x) be periodic:
Finally, continuity of the first derivative at x = a-b, again combined with the requirement that u(x) is periodic, results in:
As a result we have four homogenous equations, (7), (9), (13), and (16), with four unknowns, A, B, C, and D, for which there will be a solution if the determinant of this set of equations is zero, or:
The first row of the determinant represents equation (7), the second row is obtained by combining (13) and (7), the third row represents equation (9) and the fourth row represents equation (16). This determinant can be rewritten as two determinants, each with three rows and columns, while replacing cosb(a-b) by bc, sinb(a-b) by bs, coshab eika by ac and sinhab eika by as, which results in:
where eika + e-ika was replaced by 2coska. Since the result is independent of the sign of k, this equation also covers all solutions obtained when replacing e-ik by eik in equations (5) and (6). A further simplification is obtained as the barrier width, b, is reduced to zero while the barrier height, V0, is increased to infinity in such manner that the product, bV0, remains constant and the potential becomes a delta function train at x = a and repeated with a period of a, namely bV0 (x - b - na) where n is an integer. As b approaches zero, sinh b approaches b. Equation (20) then reduces to:
The right hand side of equation (21) shows the relation between the energy (through
Figure 4: Graph of the right hand side of equation (21) of P for P =2
|
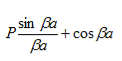 lies between +1 to -1. By varying
lies between +1 to -1. By varying 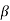 a, a wave mechanical nature could be plotted as shown in Figure, the shaded portion of the wave shows the bands of allowed energy with the forbidden region as unshaded portion.
a, a wave mechanical nature could be plotted as shown in Figure, the shaded portion of the wave shows the bands of allowed energy with the forbidden region as unshaded portion.
|
Figure 5 : Wave mechanical nature 2. With increase of
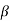 a , the allowed energy states for a electron increases there by increasing the band width of the bands, i.e., the strength of the potential barrier diminishes. This also leads to increase of the distance between electrons and the total energy possessed by the individual electron.
a , the allowed energy states for a electron increases there by increasing the band width of the bands, i.e., the strength of the potential barrier diminishes. This also leads to increase of the distance between electrons and the total energy possessed by the individual electron.3.Conversly if suppose the effect of potential barrier dominate i.e., if P is large, the resultant wave obtained in terms of shows a stepper variation in the region lies between +1 to -1. This results in the decrease of allowed energy and increase of forbidden energy gap. Thus at extremities.
Case (i) when P
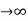 , the allowed energy states are compressed to a line spectrum.
, the allowed energy states are compressed to a line spectrum.
|
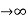
Case (ii) when P
 the energy band is broadened and it is quasi continuous
the energy band is broadened and it is quasi continuous
|
 the energy bandThe electron energy forms quasi-continuous bands (because k itself is quasi-continuous) separated from each other by a minimum gap that occurs at ka= s(s = 0, ±1, ±2, ), or k= s/a, at which the left-hand side of Equation (21) is ±1. Figure 8(b) implies that there are multiple values of k for each E. However, the Bloch theorem says that wave functions corresponding to the wave vectors k separated by m(2/a) (since b= 0) are identical, they are the same quantum state and should be counted only once. Thus, rather than plotting the energy eigenvalues for all the wave vectors, we can plot them in one period, as shown in Figure 9. This way of representation is called the reduced-zone representation. The relationship between the energy and the wave vector is the dispersion relation.
the energy bandThe electron energy forms quasi-continuous bands (because k itself is quasi-continuous) separated from each other by a minimum gap that occurs at ka= s(s = 0, ±1, ±2, ), or k= s/a, at which the left-hand side of Equation (21) is ±1. Figure 8(b) implies that there are multiple values of k for each E. However, the Bloch theorem says that wave functions corresponding to the wave vectors k separated by m(2/a) (since b= 0) are identical, they are the same quantum state and should be counted only once. Thus, rather than plotting the energy eigenvalues for all the wave vectors, we can plot them in one period, as shown in Figure 9. This way of representation is called the reduced-zone representation. The relationship between the energy and the wave vector is the dispersion relation.
|
|
|
|
|
|
|
|
|
|
|
|
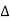 R = k
R = k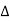 T Where
T Where 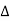 R = change in resistance
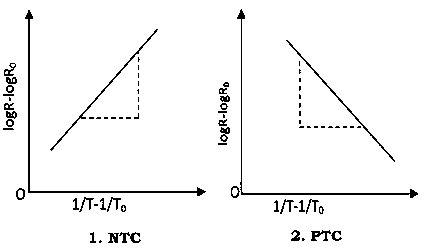
R = change in resistance T = change in temperaturek = temperature coefficient. When k is positive, it causes a linear increase in resistance as the temperature rises. This type of thermistor is generally used as a fuse. When the circuit heats up, resistance increases to prevent overload. They are also used as timing devices in televisions. When the unit is switched on, the degaussing coil is activated to eliminate the magnetic field; the thermistor automatically switches it off when the temperature reaches a certain point. Thermistor characteristics:As discussed, resistance increase with increase in temperature for PTC and resistance decrease with increase in temperature for NTC.The thermistor exhibits a highly non-linear characteristic of resistance vs temperature.
T = change in temperaturek = temperature coefficient. When k is positive, it causes a linear increase in resistance as the temperature rises. This type of thermistor is generally used as a fuse. When the circuit heats up, resistance increases to prevent overload. They are also used as timing devices in televisions. When the unit is switched on, the degaussing coil is activated to eliminate the magnetic field; the thermistor automatically switches it off when the temperature reaches a certain point. Thermistor characteristics:As discussed, resistance increase with increase in temperature for PTC and resistance decrease with increase in temperature for NTC.The thermistor exhibits a highly non-linear characteristic of resistance vs temperature.
|
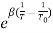 …………….(1)Where,R is the resistance of thermistor at the temperature T (in K)R0 is the resistance at given temperature T0 (in K)β is the material specific-constantThe material specific-constant of a NTC thermistor is a measure of its resistance at one temperature compared to its resistance at a different temperature. Its value may be calculated by the formula shown below and is expressed in degrees Kelvin (°K).
…………….(1)Where,R is the resistance of thermistor at the temperature T (in K)R0 is the resistance at given temperature T0 (in K)β is the material specific-constantThe material specific-constant of a NTC thermistor is a measure of its resistance at one temperature compared to its resistance at a different temperature. Its value may be calculated by the formula shown below and is expressed in degrees Kelvin (°K).Differentiating (1) w.r.t to T, we get
Taking log of (1) and simplifying we get
So
A graph plotted between
Figure 29: NTC - PTC Characteristics
|
|
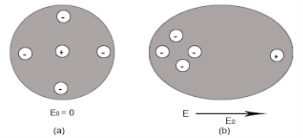
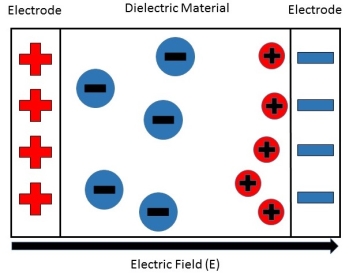
The force is only due to electron cloud acting upon nucleus would only be due to the portion of the cloud enclosed by the sphere of radius x. portion outside the sphere of radius x does not apply any force on the nucleus. Volume of the sphere of radius x = (4/3)πx3 and Volume of the sphere of radius R = (4/3)πR3 Now total negative charge of the electron cloud is -Ze …..(2) Hence, the quantity of negative charge enclosed by the sphere of radius x is, [-Ze/(4/3)πR3] * (4/3)πx3 = -Ze (x3/ R3) ……..(3) According to coulomb’s law = q1q2 /4 πR2 Charge on nucleus q2= Ze So coulomb’s force = {-Ze (x3/ R3) * Ze}/4πƐox2 = Z2e2x/4πƐo R3 ……(4) Note- magnitude is taken into account. Neglect negative sign. i.e. At equilibrium Electrostatic force = Coulomb force . EZe = Z2e2x/4πƐoR3 ……..(5) Upon simplify x = {4πƐoR3/Ze} E Now dipole moment = either charge * separation between charges i.e. x = Ze *{4πƐoR3/Ze} E = 4πƐoR3E Polarization is number of dipole moment per unit volume. Let us suppose N is the number of dipoles per unit volume so Pe=4πƐoR3EN
|
|
|
|
Hence force F1 due to electric field is F1=qE ……(1) Where q is the net charge on ion. F2 restoring force due to binding force between ions F2=kd …..(2) Where k is spring constant. Here we are considering bond as spring. k may also expressed in terms of other constant which is related to the shape of interatomic potential as young’s modulus or modulus of rigidity as k=Ydo …..(3) At Equilibrium F1 = F2 at equilibrium distance d qE = kd qE = Ydod using (3) d = Now dipole moment p= qd = q2E/Ydo …..(4) and polarization Pi = Nq2E / Ydo ……(5) This is called ionic polarization. This can also be expressed as Pi =NαiE
|
|
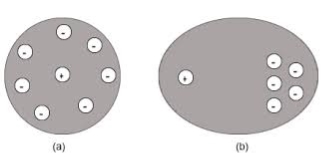
Potential energy U of the dipole moment making an angle θ with the electric field. Where p0 is the dipole moment. U=−p0⋅E=−p0Ecosθ According to statistical mechanics, the number of dipoles or molecules making an angle with the electric field is proportional to e−U/kT Letting n(θ) be the number of molecules per unit solid angle at θ, we have n(θ)=n0e+p0Ecosθ/kT
For normal temperatures and fields, the exponent is small, so we can approximate by expanding the exponential:
n(θ)= n0 (1+p0EcosθkT) To find n0 , we integrate over all angles and the result is equal to N. Where N is the total number of molecules per unit volume. The average value of cosθ over all angles is zero, so the integral is just n0 times the total solid angle 4π. We get n0=N4π or N= n0 /4π There exits molecules along the field (cosθ=1) than against the field (cosθ=−1). So in any small volume containing many molecules there will be a net dipole moment per unit volume. As dipole moment is present so polarization Pd is given
Pd =∑unitvolumep0cosθi
Evaluate Total Polarization over solid angle 2πsinθdθ. We have to integrate it
Pd = 0∫π n(θ)p0cosθ2πsinθdθ
Substitute the value of n(θ)
Pd = −N/2 −1∫1 {1+(p0E/kT)cosθ)p0cosθd(cosθ)
By integrating we get,
Pd =Np02E/ 3kT
The polarization is proportional to the field E and depends inversely on the temperature, because at higher temperatures there is more randomness by collisions. This can also be expressed as Pd =αdE
|
|
|
|
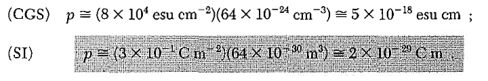 If the positive ions Ba2+ and Ti4+ were moved by
If the positive ions Ba2+ and Ti4+ were moved by 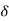 = 0.1 Å with respect to the negative O-2 ions, the dipole moment of a cell would be 6e
= 0.1 Å with respect to the negative O-2 ions, the dipole moment of a cell would be 6e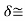 3 X l0-18 esu-cm. In LiNbO3, the displacements are considerably larger, being 0.9 Å and 0.5 Å for the lithium and niobium ions respectively, giving the larger PS.
3 X l0-18 esu-cm. In LiNbO3, the displacements are considerably larger, being 0.9 Å and 0.5 Å for the lithium and niobium ions respectively, giving the larger PS.