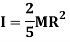Unit - 4
Centroid and Centre of Gravity
Q1) Define and explain area moment of inertia. What is radius of gyration?
A1) When a distributed loading whose intensity varies linearly acts perpendicular to an area, the computation of the moment of the loading distribution about an axis involves a quantity called the moment of inertia of the area or simply area moment of inertia.
Consider a differential plate, subjected to fluid pressure P that varies linearly with depth, as shown in fig, such that 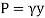 , where,
, where, 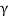 is the specific weight of fluid.
is the specific weight of fluid.

The force acting on an acting on the differential area of the plate is given by
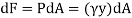
The moment of this this force about the x-axis is
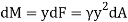
Integrating 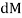 over the entire area of the plate yields
over the entire area of the plate yields
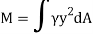
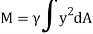
The integral part of the moment equation is called area moment of inertia about x-axis 
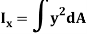
Similarly, area moment of inertia about y-axis is given as,
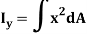
Moment of Inertia for area can also be given as
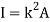
Where, A is the total area
And k is referred as radius of gyration
Radius of gyration for area of a plate about an axis is defined as the radial distance to a point which would have a same moment of inertia as the plate’s actual distribution of area, if the total area of the plate were concentrated.
It is given by,

Q2) State and explain theorem of parallel axes.
A2) Theorem of parallel axes states that “the moment of Inertia about any axis is equal to the algebraic sum of moment of inertia about the axis passing from centroid of area and the product of total area and square of perpendicular distance between the two axes.”
Mathematically,
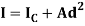
Where, 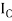 is the moment of inertia about axis passing through the centroid, and d is the perpendicular distance between two axes.
is the moment of inertia about axis passing through the centroid, and d is the perpendicular distance between two axes.
Proof:
For the system shown below,
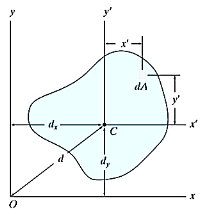
By definition of Moment of inertia,
Moment of inertia about axis x’ passing from center of gravity C is
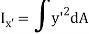
Moment of inertia about x-axis is
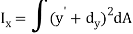
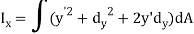
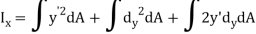
But,
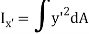
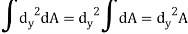
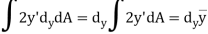
And as 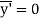 (distance between centroid and x’ axis.
(distance between centroid and x’ axis.
Hence,
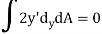
Therefore,
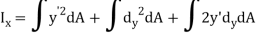
Becomes,

Similarly,

Q3) State and explain theorem of perpendicular axes.
A3) Theorem of perpendicular axes states that, “For a planar body, the sum of moments of inertia about two mutually perpendicular axes in the plane of the body is equal to the moment of inertia about an axis perpendicular to the plane of the body.”
Mathematically,
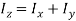
Proof:
Consider a body shown in figure,
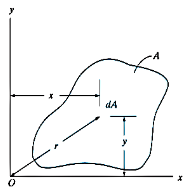
According to definition of moment of inertia,
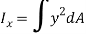

From figure,
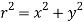
Now, according to definition, moment of inertia about an axis perpendicular to plane of body and passing through O is,
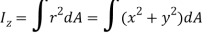
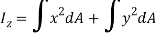
Hence,
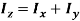
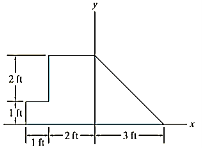
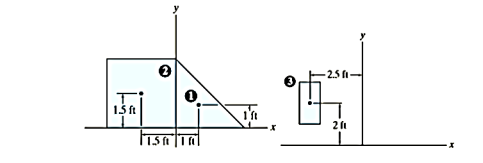
Q4) Locate the centroid of the plate area shown in Figure.
A4)
Composite parts
The plate is divided into three segments as shown in fig. Here the area of the small rectangle (3) is considered “negative” since it must be subtracted from the larger one (2).
Moment Arms
The centroid of each segment is located as indicated in the figure. Note that the 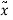 coordinates of (2) and (3) are negative.
coordinates of (2) and (3) are negative.
Summations
Taking the data from fig. The calculations are tabulated as follows
Segment | 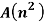 | 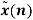 | 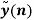 | 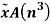 | 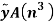 |
1 |  | 1 | 1 | 4.5 | 4.5 |
2 |  | -1.5 | 1.5 | -13.5 | 13.5 |
3 | 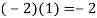 | -2.5 | 2 | 5 | -4 |
| 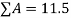 |
|
|  | 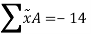 |
Thus,
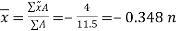
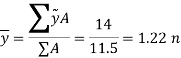
Q5) Derive the coordinates of center of gravity.
A5) A body is composed of an infinite number of particles of differential size. Consider one particle of mass 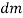 , weight
, weight 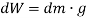 and location (
and location ( ) as shown in figure
) as shown in figure
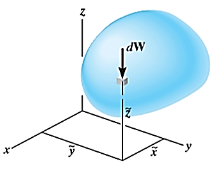
Let,  be the location of center of gravity CG of the body.
be the location of center of gravity CG of the body.
Weights of each particle will form an approximately parallel force system, and the resultant of this system is the total weight of the body W, which passes through a single point called the center of gravity G.
i.e., the weight of the body is the sum of the weights of all of its particles
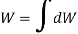
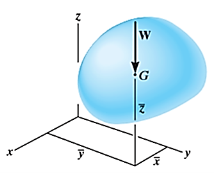
Now, the moment of W about x-axis is equal to the sum of moment of weights of each particle about same axis.
We get,
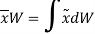
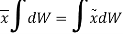
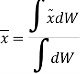
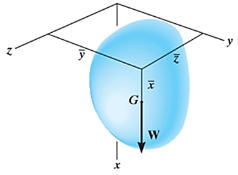
Similarly, if moments are summed about the y axis,
We get,
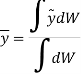
Now, consider that the body is fixed within the coordinate system and this system is rotated about the y axis as shown in fig
In similar manner, if moments are summed about the z axis, we get,
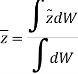
Hence, the location of center of gravity with respect to x, y, z axes is
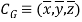

Q6) Find the moment of inertia of a rectangular section about x axis if centroid of rectangle coincides with origin of x-y plane.
A6) Consider a rectangular area of width b and depth d as shown in figure.
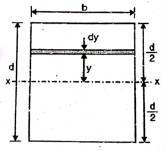
Consider an elemental strip of thickness dy parallel to x-x at a distance y from x-x.
Area of elemental strip = b dy
By definition of moment of inertia,
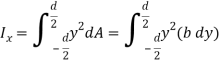
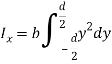
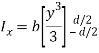

Q7) Determine the moment of inertia of the area shown in figure about the x axis.
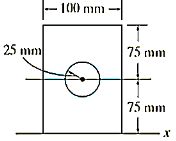
A7)
Composite parts. The area can be obtained by subtracting the circle from the rectangle shown fig. The centroid of each area is located in the figure.
Parallel-Axis Theorem.
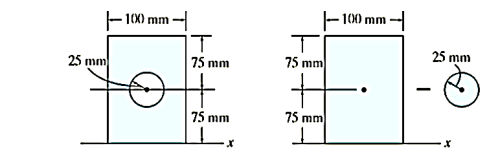
The moments of inertia about the x axis are determined using the parallel-axis theorem and the data in the table on the inside back cover.
Circle

Rectangle
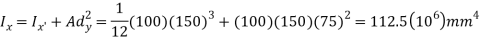
Summation
The moment of inertia for the area is therefore
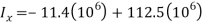
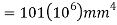
Q8) Derive the expression for mass moment of inertia of a circular plate about an axis perpendicular to plate.
A8) Consider a circular plate of thickness t and radius R rotating about z axis as shown in figure below:
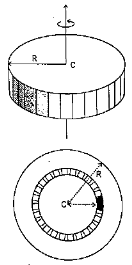
Consider an elemental strip of mass dm at distance r from CZ axis perpendicular to plane of circular plate at center C and of thickness dr.
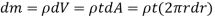
By definition of moment of inertia,
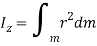
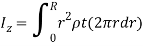
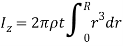
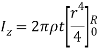
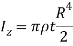
For a circular plate,
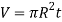 and
and 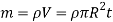
Hence,

Q9) Derive an expression for mass moment of inertia of a cone about its geometric axis.
A9) Consider a conical body of base radius R and height H rotating about its geometric axis as shown in figure.

Consider a small strip of mass dm, radius r at a distance x and thickness dx from the apex.
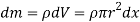
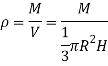
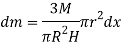

Now, from figure, we have,
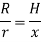
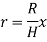
Hence,
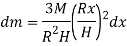

Now, moment of inertia of elemental disc about vertical axis is
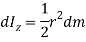

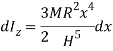
Moment of Inertia about geometric axis of cone is given by integrating above equation
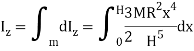
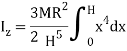
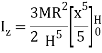
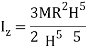
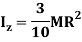
Q10) Derive an expression for mass moment of inertia of sphere.
A10) Consider a sphere of radius R and mass M as shown in figure below.
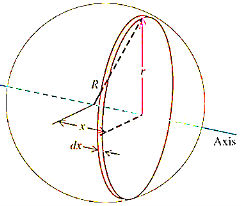
Consider a small elemental plate of mass dm, thickness dx, radius r at a distance of x from the center of sphere.
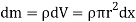
Moment of inertia of the elemental strip is,
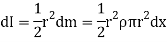
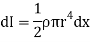
Now, from figure,
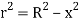
Hence,
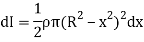
Moment of inertia of whole sphere is found by integrating moment of inertia of small elemental strip from radius -R to R
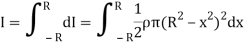
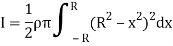
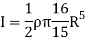
Now, we have,
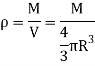
Hence, we get,