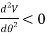Unit - 5
Virtual Work and Energy Method
Q1) Explain concept of virtual work and virtual displacement.
A1) In general, the definitions of the work of a force and a couple can be presented in terms of the actual movements which are expressed by differential displacements having values of 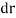 and
and 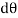 .
.
Consider now an imaginary or virtual movement of a body in static equilibrium, which indicates a displacement or rotation that is assumed and does not actually exist. This displacement is called as virtual displacement.
Virtual displacement is the displacement the force or couple would make on a body if the body was not in the static equilibrium or its motion would not be constrained.
These movements are first-order differential quantities and will be denoted by the symbols 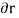 and
and  (delta r and delta
(delta r and delta 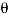 ), respectively.
), respectively.
The virtual work done by a force having a virtual displacement  is
is
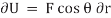
Similarly, when a couple undergoes a virtual rotation 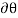 in the plane of the couple forces, the virtual work is
in the plane of the couple forces, the virtual work is
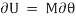
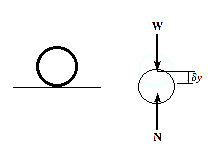
Consider a ball that rests on a floor. If there was no floor below the ball, then the ball would have been displaced due to its own weight. Then this imaginary displacement of the ball is nothing but the virtual displacement.
Q2) Explain principle of virtual work for a particle.
A2) According to the principle of virtual work if a body is in equilibrium, then virtual displacement of the body is zero for all the algebraic sum of the virtual work which is done by all the forces and moments of couple that are acting on the body. Thus,

For example, consider the free-body diagram of the particle (ball) that rests on the floor, Fig. Below. If we “imagine” the ball to be displaced downwards a virtual amount 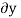 then the weight does positive virtual work
then the weight does positive virtual work 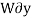 , and the normal force does negative virtual work
, and the normal force does negative virtual work 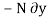 , For equilibrium the total virtual work must be zero, so that
, For equilibrium the total virtual work must be zero, so that
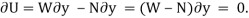
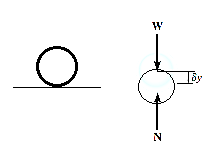
Since, 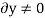 ,
,
Then, 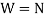 , as required by
, as required by 
As seen from the above example, no added advantage is gained by solving particle and rigid-body equilibrium problems using the principle of virtual work. This is because for each application of the virtual-work equation, the virtual displacement, common to every term, factors out, leaving an equation that could have been obtained in a more direct manner by simply applying an equation of equilibrium.
Q3) Determine the angle for equilibrium of the two-member linkage shown in Figure. Each member has a mass of 10 kg.
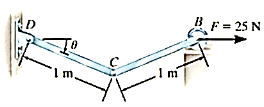
A3) Free-Body Diagram
The system has only one degree of freedom since the location of both links can be specified by the single coordinate (q=) θ. As shown on the free-body diagram in fig. When θ has a positive (clockwise) virtual rotation δθ, only the force F and the two 98.1 N weights do work. (The reactive forces 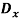 and
and 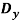 are fixed and
are fixed and 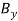 does not displace along its line of action.)
does not displace along its line of action.)



Virtual Displacements
If the origin of coordinates is established at the fixed pin support D, then the position of F and W can be specified by the position coordinates 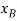 and
and  . In order to determine the work, note that, as required, these coordinates are parallel to the lines of action of their associated forces. Expressing these position coordinates in terms of θ and taking the derivatives yields
. In order to determine the work, note that, as required, these coordinates are parallel to the lines of action of their associated forces. Expressing these position coordinates in terms of θ and taking the derivatives yields

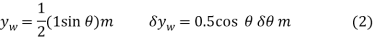
It is seen by the signs for these equations, and indicated in fig.11-6b, that an increase in θ (i.e., δθ) causes a decrease in 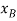 and an increase in
and an increase in 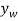 .
.
Virtual-work equation
If the virtual displacements 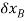 and
and 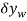 were both positive, then the forces W and F would do positive work since the forces and their corresponding displacements would have the same sense. Hence, the virtual-work equation for the displacement δθ is
were both positive, then the forces W and F would do positive work since the forces and their corresponding displacements would have the same sense. Hence, the virtual-work equation for the displacement δθ is 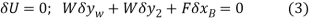
Substituting (1) and (2) into Eq.3 in order to relate the virtual displacements to the common virtual displacement δθ yields
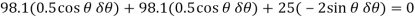
Notice that the “negative work” done by F (force in the opposite sense to displacement) has actually been accounted for in the above equation by the “negative sign” of Eq.1. Factoring out the common displacement 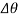 and solving for θ, nothing that
and solving for θ, nothing that  yields
yields

Q4) Determine the required force P in Figure, needed to maintain equilibrium of the scissors linkage when. The spring is unstretched when. Neglect the mass of the links.
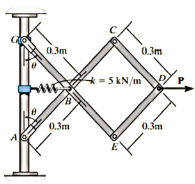
A4) Free-Body Diagram
Only 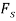 and P do work when θ undergoes a positive virtual displacement δθ, Fig. For the arbitrary position θ, the spring is stretched
and P do work when θ undergoes a positive virtual displacement δθ, Fig. For the arbitrary position θ, the spring is stretched  , so that
, so that
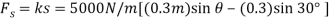
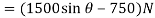
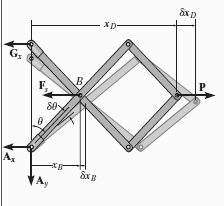
Virtual Displacements.
The position coordinates, 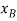 and
and 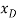 measured form the fixed point A, are used to locate
measured form the fixed point A, are used to locate 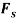 and P. These coordinates are parallel to the line of action of their corresponding forces. Expressing
and P. These coordinates are parallel to the line of action of their corresponding forces. Expressing 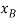 and
and 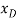 in terms of the angle θ using trigonometry,
in terms of the angle θ using trigonometry,
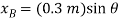
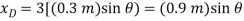
Differentiating, we obtain the virtual displacements of points B and D.
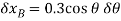 (1)
(1)
 (2)
(2)
Virtual-Work Equation:
Force P does positive work since it acts in the positive sense of its virtual displacement. The spring force 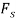 , does negative work since it acts opposite to its positive virtual displacement. Thus, the virtual-work equation becomes
, does negative work since it acts opposite to its positive virtual displacement. Thus, the virtual-work equation becomes
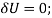
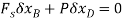
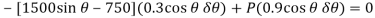
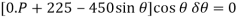
Since 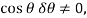 then this equation requires
then this equation requires
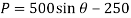
When 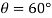
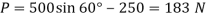
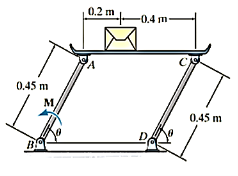
Q5) If the box in Figure has a mass of 10 kg, determine the couple moment M needed to maintain equilibrium when. Neglect the mass of the members.
A5)
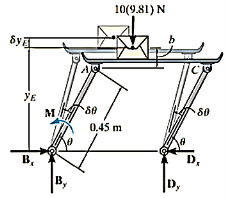
Virtual displacements:
The position coordinate 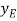 , measured from the fixed-point B, located the weight, 10(9.81) N. Here,
, measured from the fixed-point B, located the weight, 10(9.81) N. Here,
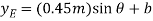
Where b is a constant distance. Differentiating this equation, we obtain
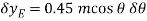 (1)
(1)
Virtual-Work Equation
The virtual-work equation becomes
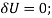
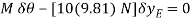
Substituting Eq.1 into this equation
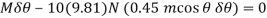
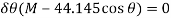
Since  , then
, then
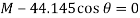
Since it is required that 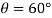 , then
, then
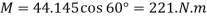
Q6) What is degree of freedom?
A6) Degree of freedom is defined as the total number of independent coordinates required to specify the complete location of every member of the structure.
Degree of freedom is also defined as number of independent motions a rigid body can have.
Consider a rigid body which is unconstrained in a 3D space have following independent motions:
- Translational motion along the three axes
- Rotational motion about its axes

It means an unconstrained rigid body in 3D space possesses 6 degree of freedom.
Now, if a rigid body is constrained to rotate in all axes, the body will have 3 degree of freedom.
If the body is restricted to have motion in a x-y plane. Then the motion the body will have is
- Translation motion in x and y axes.
- Rotation motion about z-axis.
Hence, the total maximum degree of freedom a rigid body in planar motion have is 3.
Mathematically, degree of freedom of a body in 3D space is given as,
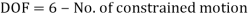
And, degree of freedom of a body in plane motion is given as,
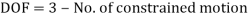

Q7) What are different types of forces acting on a rigid body? Explain Active force diagram.
A7) There are three types of forces that acts on a rigid body.
- Active forces
The forces that are responsible for work to be done are called as active forces.
- External forces – applied forces, gravitational forces
- Internal forces – spring forces, viscous forces
2. Reactive forces
The forces by the rigid body as a reaction of active forces are called as reactive forces. These are not responsible for the work
3. Internal forces
The forces in the rigid body are internal forces. These forces also don’t do any work
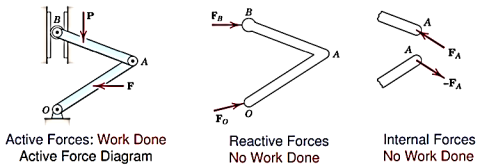
While solving the problems by the principle of virtual work, Virtual displacements are to be given carefully so that the active forces are only the known forces and the forces we are interested in obtaining.
Hence, Active force diagram are drawn which is similar to FBD.
Active force diagram (AFD) are the diagram that contains only the active forces acting on a system or a body.
Difference between FBD and AFD is explained in diagrams below.
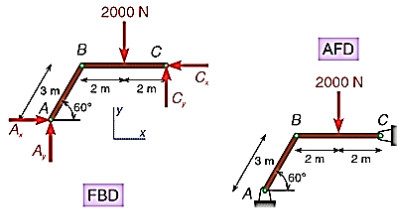
Q8) Explain Stability of equilibrium.
A8) The potential function V of a system can also be used to investigate the stability of the equilibrium configuration, which is classified as stable, neutral, or unstable.
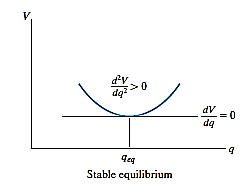
Stable Equilibrium: A system is said to be stable if a system has a tendency to return to its original position when a small displacement is given to the system. The potential energy of the system in this case is at its minimum. A simple example is shown in Fig. Below. When the disk is given a small displacement, its center of gravity G will always move (rotate) back to its equilibrium position, which is at the lowest point of its path. This is where the potential energy of the disk is at its minimum.
The graph represents stable equilibrium for one degree of freedom system.
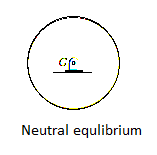
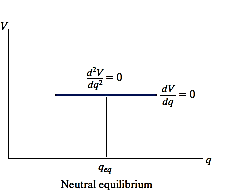
Neutral Equilibrium: A system is said to be in neutral equilibrium if the system still remains in equilibrium when the system is given a small displacement away from its original position. In this case, the potential energy of the system is constant. Neutral equilibrium is shown in Fig. Below, where a disk is pinned at G. Each time the disk is rotated, a new equilibrium position is established and the potential energy remains unchanged.
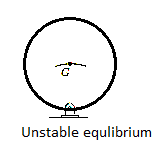
Unstable Equilibrium: A system is said to be unstable if it has a tendency to be displaced further away from its original equilibrium position when it is given a small displacement. The potential energy of the system in this case is a maximum. An unstable equilibrium position of the disk is shown in Fig. Below. Here the disk will rotate away from its equilibrium position when its center of gravity is slightly displaced. At this highest point, its potential energy is at a maximum.
Q9) If the spring AD in Figure has a stiffness of 18 kN/m and is un-stretched when, determine the angle for equilibrium. The load has a mass of 1.5 Mg. Investigate the stability at the equilibrium position.
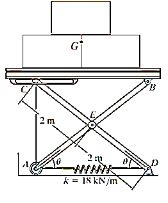
A9)
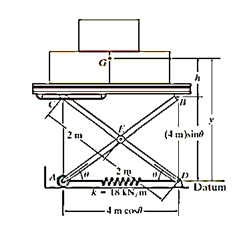
Potential energy
The gravitational potential energy for the load with respect to the fixed datum, shown in fig.
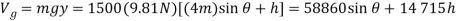
Where h is a constant distance. From the geometry of the system. The clongation of the spring when the load is on the platform is 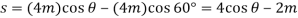
Thus, the elastic potential energy of the system is

The potential energy function for the system is therefore

Equilibrium
When the system is in equilibrium,
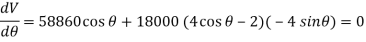
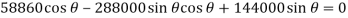
Since 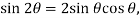

Solving by trial and error, 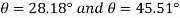
Stability.
Taking the second derivative of eq.1
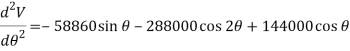
Substituting 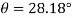 yields
yields
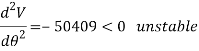
And for 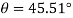
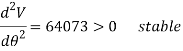
Q10) The uniform block having a mass m rests on the top surface of the half cylinder, Figure. Show that this is a condition of unstable equilibrium if h > 2R.
A10)
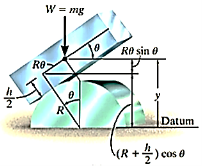
Potential function
The datum is established at the base of the cylinder, if the block is displaced by an amount θ from the equilibrium position, the potential function is
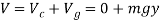
From Fig.11-18b,

Thus, 
Equilibrium position
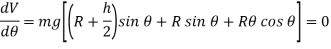
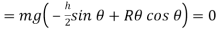
Note htat 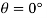 satisfies this equation.
satisfies this equation.
Stability.
Taking the second derivatives of V yields

At 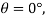
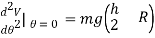
Since all the constant are postive, the block is in unstabe equilibrium provided h>2R. Because then