Unit – 8

Mechanical Vibrations

Q1) Define Vibration. Give its causes and effects.

A1) Vibration:

“Any motion which repeats itself after an interval of time is called vibration.”

E.g.: Swinging of simple pendulum

Causes of vibration:

• Unbalanced forces in the machine.
• External excitations applied on the system.
• Elastic nature of the system
• Winds, Earthquakes etc.

Effect of Vibration

Produces unwanted noise, high stresses, wear, poor reliability and premature failure of one or more of the parts.

In spite of these harmful effects, it is used in musical instruments, vibrating conveyors etc.

Q2) Explain the elements of Vibratory System

A2) Any vibratory system consists of three elements

1. Spring:For storing internal potential energy
2. Mass:For storing kinetic energy
3. Damper:For gradually dissipating energy

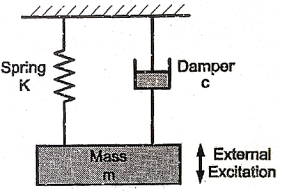
Fig. Shows a basic vibratory system. The energy enters the system with the application of external force known as external excitation. Due to excitation mass is disturbed from its mean position and mass starts vibrating between two extreme positions. During this vibrations, potential energy and kinetic energy are converted into one another periodically. Hence, system continues to vibrate.

Now, if some damper is provided to oppose the motion of mass, then some amount of energy is dissipated in each cycle due to damping effect and system decays gradually.

Q3) What is Free and Forces Vibration?

A3)

1. Free (Natural) Vibration

After disturbing the system, the external excitation is removed, then the system vibrates on its own.  This type of vibration is known as free vibrations

e.g.: Simple pendulum.

3 types: -

a) Longitudinal vibrations

When the particles of the shaft or disc move parallel to the axis of the shaft, then the vibrations are known as longitudinal vibrations.  In this case the shaft is elongated and shortened alternately and thus the tensile and compressive stresses are induced alternately in the shaft.

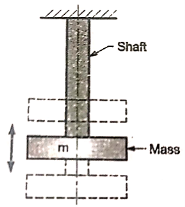
b) Transverse vibrations

When the particles of the shaft move approximately perpendicular to the axis of the shaft, then the vibrations are known as transverse vibrations.  In this case the shaft is straight and bent alternately and bending stresses are induced in the shaft.

c) Torsional vibrations

When the particles of the shaft move in a circle about the axis of the shaft, then the vibrations are known as torsional vibrations.

In this case the shaft is twisted and untwisted alternately and torsional shear stresses are induced in the shaft to.

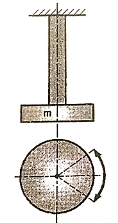
2.     Forced Vibration

The vibration which is under the influences of external force is called forced vibration.  

The external force applied to the body is periodic disturbing force created by unbalance.

The vibrations have the same frequency as the applied force. Due to the application of external forces the amplitude of these vibrations is maintained almost constant.             

Q4) Formulate differential equation of motion for undamped free vibration.

A4)

1. Newton Method

A spring mass system as shown in Figure

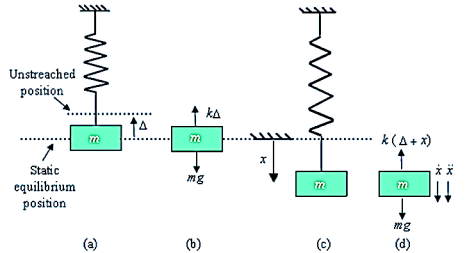
The direction of x in the downward direction is positive. Also, velocity, 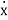, acceleration, 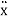, and force, F, are positive in the downward direction

According to D’Alembert’s Principle, a body or a system which is not in static equilibrium due to acceleration it possesses, can be brought to static equilibrium by introducing the inertia force on it.

From Figure (d) on application of Newton's second law, we have

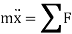
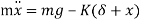
From fig (b) we have

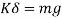
i.e., spring force due to static deflection is equal to weight of the suspended mass

So, the above equation becomes 

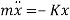
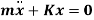
2.     D’Alembert’s Method

According to D’Alembert’s Principle, a body or a system which is not in static equilibrium due to acceleration it possesses, can be brought to static equilibrium by introducing the inertia force on it.

By D’Alembert’s Principle

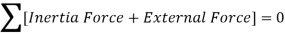
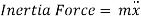
From fig (d)

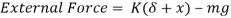
Therefore,

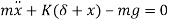
From fig (b) we have

We get,

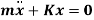
3.     Energy Method

In a conservative system (i.e., with no damping) the total energy is constant, and differential equation of motion can also be established by the principle of conservation of energy.

By law of conservation of energy

Total Energy = Constant

KE + PE = Constant

The equation will be given as

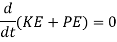
Kinetic Energy is given as

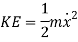
Potential energy PE is stored in the form of strain energy in elastic deformation

Therefore,

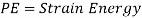
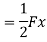
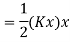
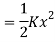
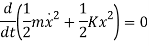
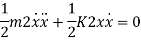
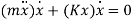
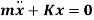
Q5) A 200-kg machine is placed at the end of 1.8-m-Iong steel cantilever beam. The machine is observed to vibrate with a natural frequency of 21 Hz. Find the equivalent stiffness of the system.

A5) The natural frequency of the system is

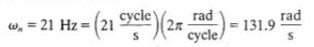
Also,

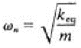
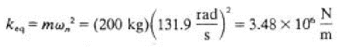
Q6) What is degree of freedom?

A6) The minimum number of independent co-ordinates required to specify the motion of system at any instant is known as degrees of freedom.

It is equal to the number of independent displacements that are possible.  This number varies from zero to infinity.

Zero degree of freedom

The body at rest is said to have zero degree of freedom.

Single Degree of freedom

Here there is only one independent co-ordinate to specify the configuration.

E.g.: A mass supported by a spring.

Two degrees of freedom

There are two independent co-ordinates to specify the configuration.

E.g.: Springs supported Rigid mass. (It can move in the direction of springs and also have angular motion in one plane)

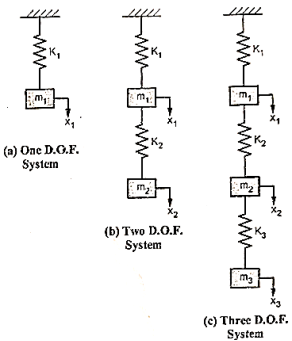
Multi degrees of freedom

A cantilever beam has infinite degrees of freedom.

Q7) Derive expression for frequency and amplitude of free vibrations without damping and single degree of freedom system

A7) We have equation of motion

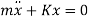
Or

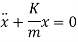
We have fundamental equation of SHM as

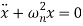
Where 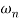is the natural frequency (in rads/sec)

By comparing Equation of motion and fundamental equation of SHM, we get

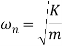
This Equation satisfies the simple harmonic motion condition.

The undamped free vibration executes the simple harmonic motion as shown in Figure

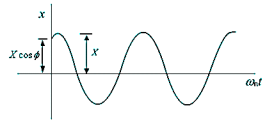
Since sine & cosine functions repeat after 2π radians (i.e., Frequency   Time period = 2 π), we have

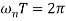
The time period (in second) can be written as

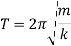
The natural frequency (in rad/sec or Hertz) can be written as

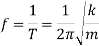
Also, we have,

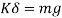
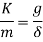
Therefore,

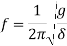
Now, solution for the differential equation 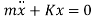is

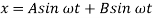
Or

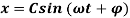
Where,

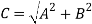
And

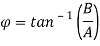
Where, A and B are constants found using the initial conditions.

Q8) Write a note on simple pendulum.

A8) A simple pendulum, consists of heavy mass which is suspended at the end of a light inextensible and flexible string. The other end of the string is fixed to a rigid support O as shown in figure below.

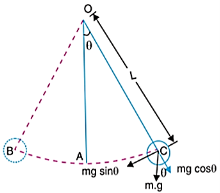
Let L be the length of string and m be the mass of bob suspended at one end of string.

Weight of bob, W = mg

Let the string is suspended through small angle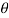

The couple tending to restore the mass to the equilibrium position A or simply restoring torque is given by,

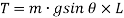
Since 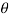is very small, 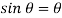rad

Hence,

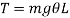
Mass moment of inertia of simple pendulum about an axis through point of suspension O is given by

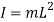
Angular acceleration of string is given by,

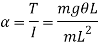
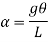
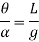
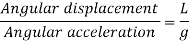
Time period in SHM is given by,

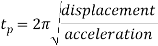
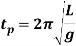
And frequency of oscillation is

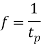
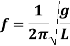
From the above equations, it can be concluded that the periodic time and the frequency of oscillation of a simple pendulum depends only upon its length and acceleration due to gravity. The mass of the bob has no effect on it.

Q9) Derive expression for time period and frequency of compound pendulum.

A9) When a rigid body is suspended vertically along a fixed point, and it oscillates with a small amplitude under the effect of gravity, the body is known as compound pendulum.

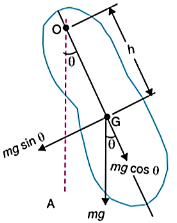
Let,

m = mass of rigid body

k = radius of gyration about axis perpendicular to plane of motion and passing through CG of body

h = distance of CG from point of suspension O

Weight of body, W = mg

If the pendulum is given small angular displacement 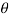, then couple tending to restore the body in the equilibrium position OA or simply restoring torque is given by,

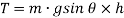
Since 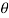is very small, 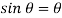rad

Hence,

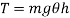
Mass moment of inertia of pendulum about an axis through point of suspension O is given by

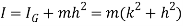
Angular acceleration of string is given by,

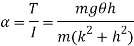
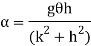
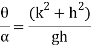
Time period is given by,

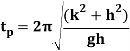
And frequency of oscillation is

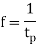
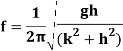
Q10) Derive expression for time period and frequency of torsion pendulum.

A10) It is also referred as trifilar suspension. In torsional pendulum a body (disc or flywheel) is suspended by three long flexible wires A, B and C, as shown in Figure below.

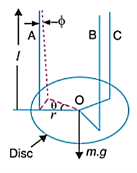
When the body is twisted about its axis through a small angle θ and then released, it will oscillate with simple harmonic motion.

Let,

m = mass of suspended body

W = mg = weight of body

K = radius of gyration of body about an axis perpendicular to plane of motion (twist) and passing from CG of body.

L = length of each wire

r = distance of wire from the axis of disc

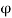= corresponding angular displacement of wire.

Moment of inertia of the body is given by,

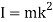
From figure, for small displacements,

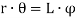
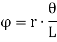
Since the three wires are attached symmetrically with respect to the axis, therefore the tension in each wire will be one-third of the weight of the body.

Hence, tension in each wire is,

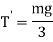
Component of the tension in each wire perpendicular to r

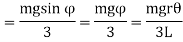
(Since 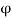is very small, )

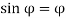Torque applied to each wire to restore the body to its initial equilibrium position (i.e., restoring torque) is

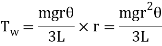
Hence, Total restoring torque applied to three wires is

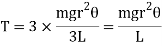
The inertial torque is given by,

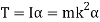
Hence,

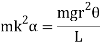
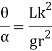
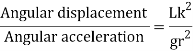
Time period is given by,

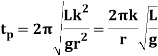
And frequency of oscillation is

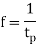
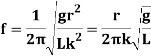
Q11) Give the uses of simple, compound and torsion pendulums.

A11) Pendulums has many applications in various fields. Some of the common uses of different pendulums are mentioned below:

1. Use of simple pendulum

• The most common use of simple pendulum is observed in clocks. It is used in keeping time.
• Simple pendulum is also used in the measurement of vibration like earthquake. Difference in the movements of simple pendulum is recorded for the measurement of vibrations.

2.     Use of compound pendulum

• It is used to find the acceleration due to gravity at different altitudes and latitudes of earth.
• It is also used to find moment of inertia and radius of gyration of rods

3.     Use of torsion pendulum

• Torsion pendulum is used to find moment of inertia and radius of gyration of a planar body like disc or flywheel. The body (say a disc or flywheel) whose moment of inertia is to be determined is suspended by three long flexible wires.
• It is also used to find the modulus of rigidity for different materials.