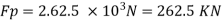Unit - 6
Dimensional Analysis and Hydraulic Similitude
Q1) Explain dimensional homogeneity?
A1)
P = w h
Dimensions of LHS = ML-1T-2
Dimensions of RHS = ML-2T-2×L = ML-1T-2
Dimensions of LHS = Dimensions of RHS
Hence, equation P= w h is dimensionally homogeneous; so it can be used in any system of units.
Applications of Dimensional Homogeneity:
Q2) Explain Rayleigh methods?
A2)
Procedure:
Procedure of Rayleigh method are given below
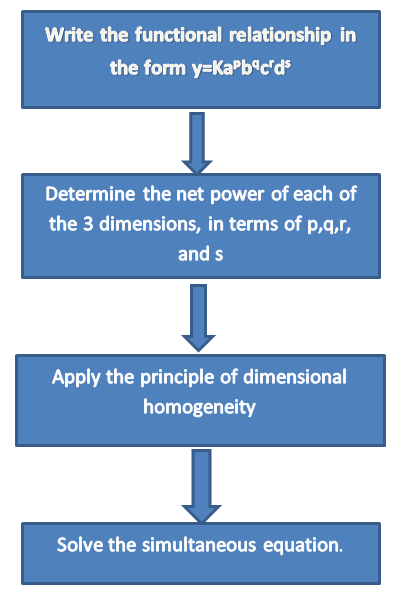
Fig no 1 Procedure of Rayleigh method
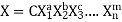
Where C = dimensionless constant
a, b, c,..m are arbitrary exponents.
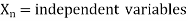
1. Example: The rate at which a pressure wave propagates through a liquid can be expected to depend on the quantity of liquid represented by the bulk modulus K, and its mass established by D. A. the type of relationship that exists.
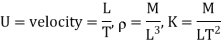


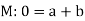
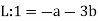
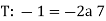
Therefore: 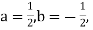 and a possible equation is
and a possible equation is
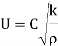
Q3) Explain Buckingham pi methods and other methods?
A3)
“If there are n variables in a dimensionally homogeneous equation and if these variables contain fundamental dimensions (such as M, L, T, etc.) then the variables are arranged into (n-m) dimensionless terms.
Mathematically, if any variable X1, depends on independent variables, X2, X3, X4,…… Xn; the functional equation may be written as
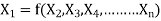 -------- 1
-------- 1
Equation 1 can also be written as
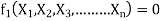 -------- 2
-------- 2
It is dimensionally homogeneous equation and contains n variables.
If there are m fundamental dimensions, then according to Buckingham’s Π – theorem, it [equation] can be written in terms of number of Π – terms in which number of Π terms is equal to (n-m).
Hence equation 2 becomes as
 --------3
--------3
Each dimensionless 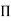 – term is formed by combining m variables out of the total n variables with one of the remaining (n-m) variable.
– term is formed by combining m variables out of the total n variables with one of the remaining (n-m) variable.
These m variables which appear repeated in each of  – terms are consequently called repeating variables and are chosen from among the variables such that they together involve all the fundamental dimentions and they themselves do not form a dimensionless parameter.
– terms are consequently called repeating variables and are chosen from among the variables such that they together involve all the fundamental dimentions and they themselves do not form a dimensionless parameter.
Let in the above case X2, X3 and X4 are the repeating variables if the fundamental dimensions m(M, L, T) = 3, then each term is written as:
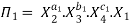
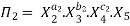
.
.
.
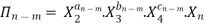 -------- 4
-------- 4
Where a1, b1, c1, a2, b2, c2 etc. are the constants, which are determined by considering dimensional homogeneity. These values are substituted in equation 4 and values of 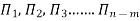 are obtained. These values of Π’s are substituted in equation 3.
are obtained. These values of Π’s are substituted in equation 3.
The final general equation for the phenomenon may then be obtained by expressing anyone of the Π – terms as a function of the other as:
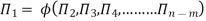

Q4) Explain dimensionless groups?
A4)
The following table lists the seamless groups most closely associated with heat and high transfer.
Archimedes Number | 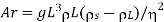 |
|
Bond number | 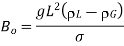 | Also called Eotvos number, Eo |
Biot number, heat transfer | 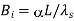 |
|
Biot number, mass transfer | 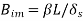 |
|
Clausius number | 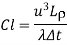 |
|
Darcy number |  | Alternative 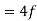 |
Deborah number | 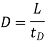 | Relaxation time/ observation time, also called Weissenberg number also called Brinkam number. |
Eckert number |  |
|
Euler number | 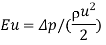 |
|
Fanning friction factor | 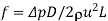 |
|
Fourier number, heat transfer | 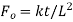 |
|
Fourier number, mass transfer |  |
|
Froude number |  | Or 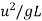 |
Galileo number | 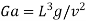 | 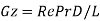 |
Graetz number |  | Also called phase change number |
Grash of number |  | 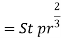 |
Jakob number | 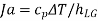 |  |
J factor, heat transfer | 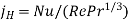 |
|
J factor, mass transfer |  |
|
Kutataeladze number | 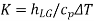 |
|
Lewis number |  | 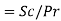 |
Mach number | 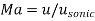 |
|
Nussett number | 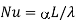 |
|
Preclet number | 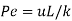 | 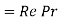 |
Prandtl number | 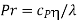 | 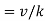 |
Rayleigh number | 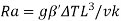 | 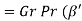 |
Reynolds number |  |
|
Schmidt number | 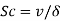 |
|
Sherwood number | 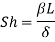 |
|
Stanton number, heat transfer | 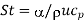 | 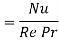 |
Stanton number, mass transfer | 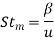 | 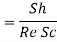 |
Strouhal number | 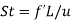 | f’ is frequency |
Weber number | 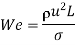 |
|
Fig no 2 The seamless groups most closely associated with heat and high transfer.
Q5) What is similitude?
A5)
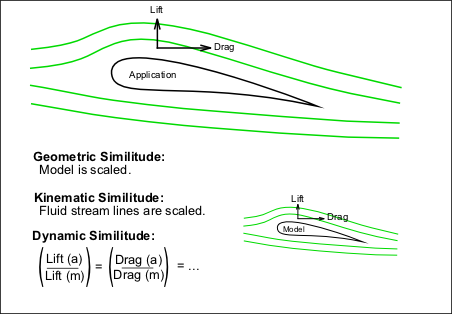
Fig no 3 Three conditions are required for the model to match the system.
The following methods are needed to achieve similarity;
Geometric Similarity - the model is the same method as the system, which is usually measured.
Kinematic similarity - the fluid flow of both the model and the actual application must exceed the same levels of motion change time. (liquid distribution is the same)
Dynamic similarity - the ratio of all forces acting on liquid-related particles and parameters in both systems remains the same.
To satisfy the above conditions the application is analyzed;
Q6) Explain model studies?
A6)
In short, experimenting with the model has become an important tool for the design engineer.
Model courses are designed for two purposes, namely -
(i) Obtaining information on possible performance of the species, also
(ii) Assist in the construction and avoidance of costly errors and transform the economic solution to the hydraulic problem.
Q7) Explain type of models?
A7)
The classification of models is
i. Undistorted models
ii. Distorted models
Undistorted model
If the average size of the model is the same size and type of the same condition, the model is said to be uninterrupted model.
Distorted model
The inverted model is said to be a distorted model only if it differs geometrically and prototype.
Advantages of distorted models
The advantages of distorted models are,
1. The exact size of the model can be accurately measured.
2. Model costs can be reduced.
3. Incredible flow in the model can be maintained.
Q8) Explain type of model and application or dimensional analysis and model studies to fluid flow problem?
A8)
Types of model laws
Types of model laws are
1. Reynolds model laws
2. Froude model laws
3. Euler model laws
4. Weber model laws
5. Mach model laws
Application of Froude model laws
The law of Froude's model is applied
1. Free local flow such as streaming to spill, heirs, sluices, channels etc.
2. Flow of the jet from the orifice or nozzle
3. Where waves may form more
4. When a flow of liquid of different strength passes one anther
Weber model laws
When only strong surface strength is the main model can be considered to be strongly similar to the prototype whereas the inertial ratio and surface tensile strength are the same in model and prototype.
(We) model = (We) prototype
Use of dimensional analysis
1. Conversion from one unit to another
2. Testing of statistical units (Size Relationship)
3. Define unparalleled relationships using
a) Rayleigh's method
b) Buckingham TT-Theorem
4. Model Analysis
Reynolds Model Law
In flow situations where in addition to inertia, viscous force is the other predominant force, the similarity of flow in the model and its prototype can be established if Reynolds number is same for both the systems.
This is known as Reynolds law and according to this law,
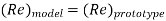
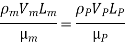
Where, ρm = density of fluid in model
Vm = velocity of fluid in model,
Lm = length of linear dimension of the model, and
µm = viscosity of fluid in model
And ρ P, VP, LP and µP are the corresponding values of density, velocity, linear dimension and viscosity of fluid in prototype.
Or 
Or 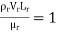
[ 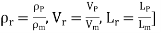
Following are some of the phenomenon for which Reynolds model law can be a sufficient criterion for similarity of flow in the model and the prototype:
Froude Model Law
When the gravitational force can be considered to be the only predominant force which controls the motion in addition to the inertia force, the similarity of the flow in any two such systems can be established if the Froude’s number of both the systems is the same.
This is known as Froude’s Model Law.
Some of the phenomenon for which the Froude Model Law can be sufficient criterion for dynamic similarity to be established in the model and the prototype are:
Let, Vm = velocity of fluid in model
Lm = length (or linear dimension) of the model
gm = acceleration due to gravity (at a place where model is tested)
and VP, LP and gP are the corresponding values of the velocity, length and acceleration due to gravity for the prototype.
Then according to Froude Law,
(Fr)m = (Fr)P
Or 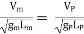 ------ 1
------ 1
As the value of g at the site of mode testing will be practically the same as at site of the proposed prototype, therefore gm = gP and the equation 1 values as
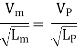
Or 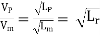
Where Lr = scale ratio for length
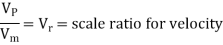
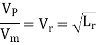
Q9) Explain dynamic similitude of Reynolds, Froude, mach, weber, euler number?
A9) Reynold’s Number (Re)
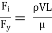
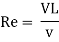
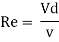
Fraud’s Number (Fr)
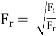
Euler’s Number (Eu)
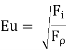
Weber’s Number (We)
Mathematically, 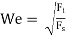
i) Flow of blood in veins and arteries
ii) Liquid atomisation, and
iii) Capillary movement of water in soils
Mach Formula (M)
Mathematically, 
Q10) An oil of specific gravity 0.9 and viscosity 0.9 poise is to be transported at the rate of 1000 l/s through a. 1.2 m diameter pipe. Tests were conducted on a 10 cm diameter pipe using water at .20°C. Viscosity of water at 20°C is 0.01 poise. Find the rate of flow in the model.
A10)
Prototype
D = 1.2 m.
Sp = 0.9,
Model
Dm = 10 cm = 0.1 m
Sm = 1
μp = 0.9 poise. μm = 0.01 poise = 1 x 10-² poise
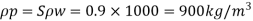
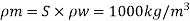
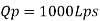
To find: Velocity and flow rate.
Since it is pipe flow, Reynolds’s number must be applied.
(Re)model = (R) prototype
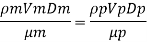
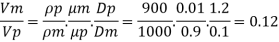
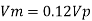
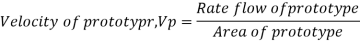

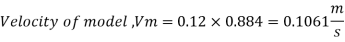
Rate of flow through model
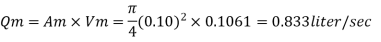
Q11) From the following data, find the scale ratio of model Velocity of water 1 m/'s through circular pipe. Prototype: Velocity of oil 0.12 ms through 50 mm diameter pipe. Assume kinematic viscosity of water 0.01 cms and that of oil 0.008 cm/s. Assume dynamic similarity. Also find the diameter of pipe used for model.
A11)
Prototype
Vp -012 m/s
Dp = 50mm = 0.05 m
Vp = 0.006 cm²/sec
Model
Vm= 1m/s
Dm=?
Vm= 0.01 cm^2/sec
To find:
Since it is pipe flow, Reynold's ember mast be applied

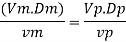
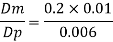
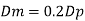
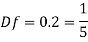
Model scale ratio is 1:5
Now, diameter of model pipe
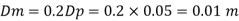
Q12) Water at 15.6°C flows at 3.5 m/s in a 150 mm diameter pipe. At what velocity must a fuel oil at 32.6°C flow in a 75 mm diameter pipe for the flow to be dynamic similar? v.-1.13 x 10 m/s and 2.96 x 10 m/s.
A12)
Water
Dw = 150 mm = 0.15 m
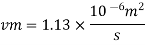

Oil
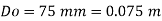
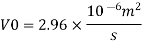
To find: Velocity of oil V.
Since it is pipe flow, Reynold's number must be applied
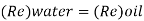
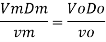
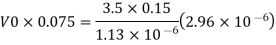
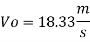
The velocity of cl at 32.6°C is 15.33 m'k
Q13) A ship has a length of 150 m and wetted area 3000 m² A model of this ship 5 m in length when towed in fresh water (p= 1000 kg/m) at 2 m/s produces a resistance of 40N. Calculate (1) corresponding speed of the ship. (i) the shaft power required to propel the ship at this speed through sea water (p=1030 kg/m). Take the propeller efficiency as 75%
A13)
Model
Lm= 5 m
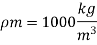
Vm= 2 m/s
Fm = 40 N
Prototype
Lp= 150 m

Ap= 3000m^2
Propeller efficiency= n= 75 %
To find:
Speed of ship Vp
Since it is ship motion Reynolds number must be applied
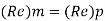
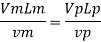
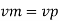
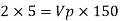
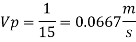
Ratio of drag force
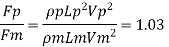
Drag force on prototype
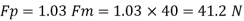
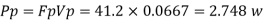
Actual power input

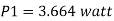
Q14) A ship 300 m long moves in seawater whose density is 1030 kg/m A1.75 Model of this ship is to be tested in a wind tunnel. The velocity of air in wind tunnel is 29 m/s the resistance of the model is 60 N. Determine velocity and resistance of the ship in seawater. Air density is 1.24 kg/m Kinematic viscosity of air=0.018 stokes Kinematic viscosity of seawater 0,01 stokes.
A14)
Given:
Prototype
Scale 1:75
Lp = 300 m
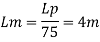

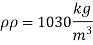
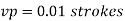
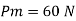
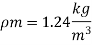
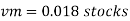
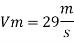
To find:
Vp and Fp
Since it is ship motion Reynolds number must be applied
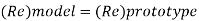
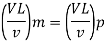
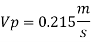
Drag force ratio
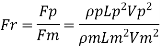
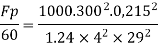
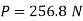
Q15) In a geometrically similar model of weir the discharge is 0.15 m².s.. if the scale of the model is 1/50 find the discharge of the prototype.
A15)
Given:
Discharge per meter length = 0.15 m/sec.
Scale ratio Lr = Lp/Lm = 50
To find: qp
Since it is a spillway, Froude Number must be applicable.
The discharge ratio for spillway is given by
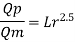
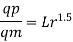
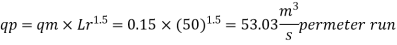
Q16) The performance of a spillway is to be studied by means of a model constructed to a scale of 1:9. Determine: (1) Rate of flow in the model for a prototype discharge of 1400 m/s. (2) Energy lost in the prototype if the energy loss in model is 0.3 kW
A16)
Given:
Scale of model 1:9
Lr = 9
Discharge of proto type Q = 1400 m^3 /s
Since it is a spillway, Froude number must be applicable.
Using discharge scale ratio
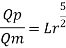

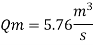
Energy loss
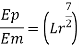
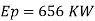
Q17) In the model test of a spillway the discharge per meter length is 1/6 m^3/sec if the scale of the model is 1/36 find the discharge per meter run of the prototype.
A17) Given:
Qm = 1/6 m^3/sec
Lr = Lp/Lm = 36
To find: QP
Since it is a spillway, Froude Number must be applicable. The discharge ratio for spillway is given by
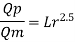
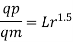
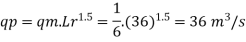
Q18) Find the suitable scale for model of a spillway if maximum discharge available in the laboratory is 10 L.P.S. and the prototype discharge is 168.07 m/sec.
A18)
Given:
Q=10 lps = 10 x10³ m³/sec;
Qp = 168.07 m^3/sec
Since it is a spillway, Froude Number must be applicable. using discharge scale ratio
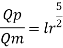
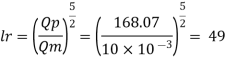
Model scale should be 1:49.
Q19) A ship model of scale 1/60 is towed through sea water at a speed of 1:1 m/s A force of 2.1 N is required to tow the model. Determine the speed of ship and the propulsive force on the ship if the prototype is subjected to wave resistance only.
A19)

Speed of model Vm=1.1 m/s
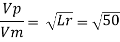
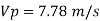
Resistance to prototype in sea water