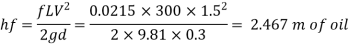Unit - 8
Turbulent Flow
Q1) Explain Reynolds experiment?
A1) The process of conducting laboratory research to find out the significant number of Reynolds pipe flow in various discharge cases is described in this article.
Reynolds number is the ratio of the unbalanced energy of a liquid to the energy of a viscous fluid. Non-liquid energy can be expressed by:
Inertia force, Fi = mass × acceleration
= (density × volume) X (Velocity / time)
= (density X Area) X (Velocity X Velocity)
F I = 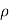 A V 2
A V 2
Viscous strength, Fv = Shear stress X area
F v =  v D
v D
Therefore, Reynolds' number is provided by:
R e = F I / F v = 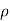 A V 2 /
A V 2 /  v D = rho v D /
v D = rho v D / 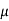 = v D /
= v D / 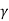
Where, v = velocity of flow fluid
D = width of glass metal
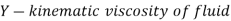
Apparatus required

Fig no 1 Reynolds experiment apparatus
Test Process
The Reynolds test process is as follows:
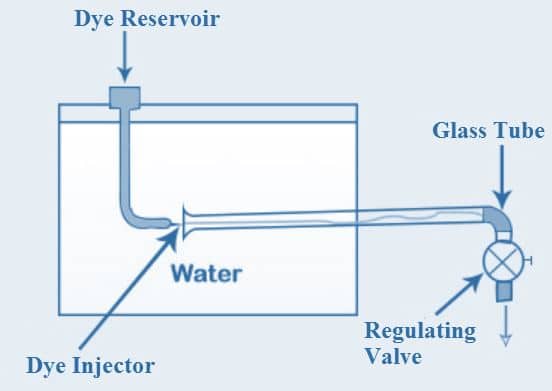
Fig no 2 Operational Status of Reynolds Resources
Calculation
The volume of water collected in a tank in t seconds, V = tank area X Water level in t seconds
Release, Q = Volume / time
Velocity of flow, v = Extrusion / location of glass tube
Reynolds number, Re
Q2) Explain transition from laminar to turbulent flow?
A2)
Transition stages in boundary layers
Fig no 3 The path from receptivity to laminar turbulent transition
The boundary layer can change into chaos in many ways. Which path is physically visible depends on the initial conditions such as the initial height of the disturbance and the size of the area. The level of understanding of each phase varies greatly, from a complete understanding of the development of the basic mode to a complete penetration of the understanding of the transit patterns.
Receptivity
Primary mode growth
Simple harmonic boundary layer sound in the physics of transition to turbulence
Second instability
Q3) Explain definition of turbulence, Scale and intensity of turbulence and causes of turbulence?
A3) DEFINITION OF TURBULENCE
SCALE AND INTENSITY
In reporting a disturbance, it is often considered light, moderate, severe or extreme. The level is determined by the type of initial agency and the level of air stability.
Light turbulence
A slight turbulence temporarily causes a slight change in height and / or attitude or a slight explosion. Airplane occupants may feel overwhelmed when faced with their seat belts.
Moderate
The moderate chaos is similar to a small chaos but more intense. However, there is no loss of flight control. Employees will experience obvious difficulties in their seat belts and unprotected items will be released.
Severe turbulence
Severe turmoil creates a dramatic and sudden change in altitude and / or attitude, and, more often than not, a significant variation in the airspeed shown. The flight may be temporarily out of control. The crew will be forced to violently fasten their seat belts.
Extreme turbulence
In the worst case scenario, the plane is thrown violently and it is impossible to control it. It can cause structural damage.
Chop is a type of disorder that causes a rapid and rhythmic eruption
CAUSES OF TURBULENCE
There are four causes of unrest.
1. Mechanical turbulence

Fig. Mechanical turbulence
Favorable mountain wave conditions include:
crossing over or over the mountain, a layer of low stability near the earth, a very stable layer at the top of the mountain above the upper layer, and finally, the unstable layer over the unstable layer) -
This requires air parcels to be forced to rise above the mountain peaks to sink at their first elevation (or at the level of equilibrium)
The parcels then get up and fall into the oscillatory pattern, similar to a heavy spring
- Cirrocumulus Standing Lenticular (CCSL)
- Altocumulus Standing Lenticular (ACSL) closely related
- Rotor Clouds (tense frequency)
2. Thermal turbulence
Fig. Thermal turbulence
3. Frontal turbulence
The rising air temperature in the front slope and the friction between these opposing wind bodies create tension in the front area. This disorder is most pronounced when warm air is moist and unstable and will be more severe when thunderstorms occur. Confusion is often associated with colder climates but can be, to a lesser extent, warmer.
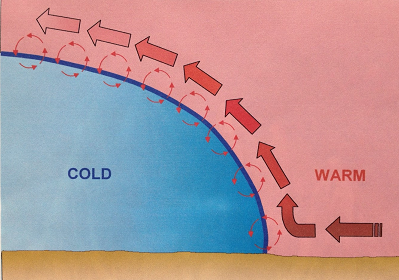
Fig. Frontal turbulence
4. Wind shear
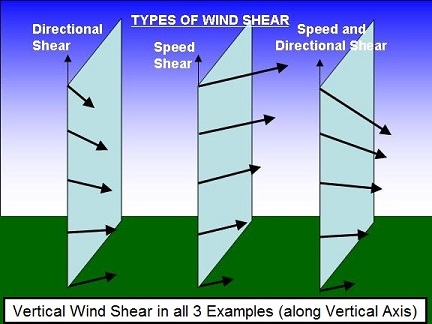
Fig. Wind shear
Q4) Explain instability in turbulence?
A4) Liquid instability is evident everywhere in nature. The flow of fluid will begin in the laminar and is smooth and then progress quickly to the wrong pattern and eventually to the chaos.
Q5) Explain mechanism of turbulence and effect of turbulent flow in pipes?
A5) Mechanism of Turbulence

Fig no 8 Mechanism graph of turbulence
Effect of Turbulent Flow in Pipe
Interaction Effect
Condensation Effect
Aerodynamic and thermal losses in turbine phases, due to the presence of phase two and the effects of turbulence, are as follows:
The effect of direct loss in non-equilibrium flow increases with the number of phases and reaches its end at the end of the steam turbine. Indirect losses cause a change in aerodynamic loss from equilibrium.
Some details of the two turbine flow areas are as follows:
Q6) Explain Reynolds stresses and semi empirical theories of turbulence?
A6) REYNOLDS STRESSES
The applied energy (in each area) is set in the flow that you mean by the volatility of the chaos.
They come from an offline advertising temple where Navier - Stokes' Reynolds figures are rotten and Reynolds is limited. The standard form of Reynolds stress tensor is
T i j = - 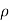 u I u j
u I u j
Kinematically, speed mixing -
uI u j
Represents the flow of pressure on the side
X i
Across the plane in the direction
X j
Or flow of pressure to the side
X j
Across the plane in the direction
X i
In a turbulent flow, the Reynolds pressure diversification leads to the proposed energy budgets. They are usually more orders of magnitude than viscous pressure. In the boundary line, Reynolds' most important pressures are the direct currents of the horizontal pressure,
- 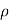 u w
u w
And
- 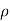 v w
v w
SEMI-EMPIRICAL THEORIES OF TURBULENCE
Q7) Explain prandts mixing length theory?
A7) According to Prandtl, the mixing length (l) is defined as the average lateral distance through which a small mass of fluid particles would move from one layer to the other adjacent layers before acquiring the velocity of the new layer.
He assumed that components u' and v' are of the same order and the velocity fluctuation in x direction is related to the mixing length as
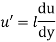
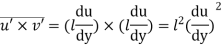
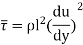
When the viscous action is also included, the total shear stress may be expressed as
Above is used for most of the turbulent flow problems for determining the shear stress.
Q8) Explain universal velocity distribution equation?
A8)
Fig no 9 Velocity Distribution in Broadcasting
Thermodynamic Description of Leopold's Principle
The application of Leopold's principle to dynamic energy in a dynamic sense
Fig. Leopold principle and Prandtl deflection
Q9) Explain resistance to flow of fluid on smooth and rough pipes?
A9)
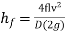
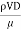

Where, D = Diameter of the pipe
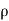 = Density of the fluid.
= Density of the fluid.
 = Dynamic viscosity of the fluid.
= Dynamic viscosity of the fluid.
K= average height of pipe wall roughness protrusions.
The term K / D is commonly known as relative roughness.
The equation 1 general equation which is applicable to laminar as well as turbulent flow in pipes .
Variation of friction coefficient f for smooth pipe-
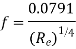

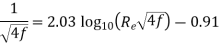
Nikuradse’s experimental result for turbulent flow in smooth pipe For Re = 5×10⁴ to Re as high as 4 × 107 for f is
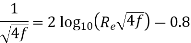
f = 
Variation of friction coefficient f for rough pipes

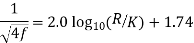
Q10) Explain moody diagram?
A10)
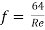
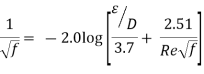
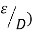
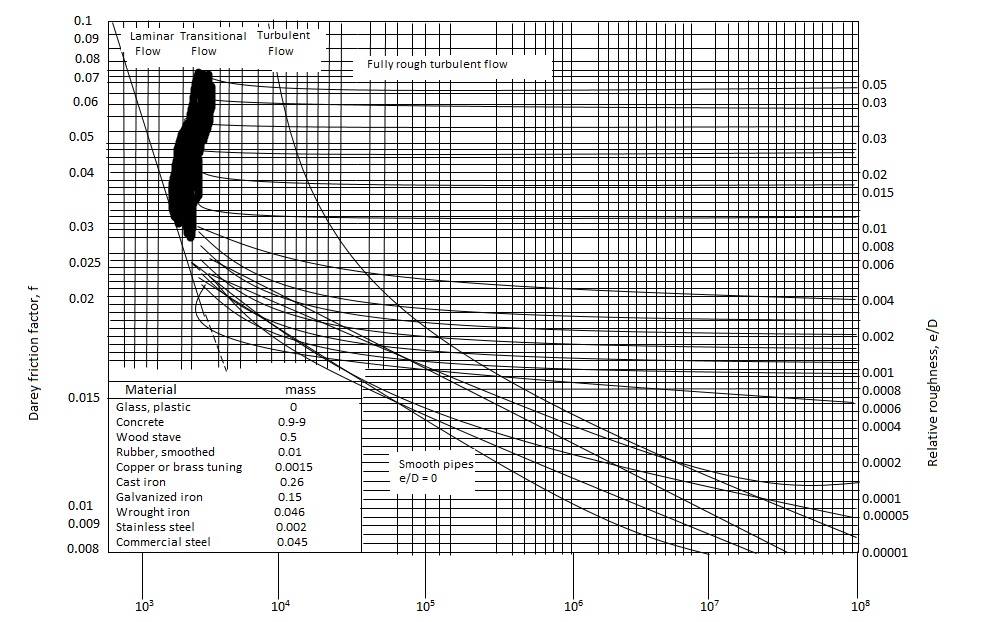
Fig no Moody chart
Q11) A pipeline carrying water has average height of irregularities projecting from the surface of the boundary of the pipe as 0.12 mm. What type of boundary is it? The shear stress developed is 4.9 N/m2. The kinematic viscosity of water is 0.01 strokes.
A11)
Given
Height of irregularities k= 0.15 mm

Shear stress 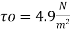
Kinematic viscosity 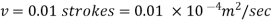
Density of water 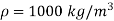
Step 1 Shear stress
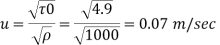
Step 2 Roughness Reynolds’s number
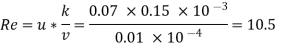
Since Re > 4 but less than 100 the surface is transition
Q12) For turbulent flow through a pipe having wall shear stress 10 N/m², size of surface imperfection is k = 0.03 mm. Assuming the kinematic viscosity of water 1 x 10 m³/sec. find whether pipe behave as hydro dynamically rough, smooth or transitional.
A12)
Given: Shear stress 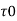 = 10 N/m²
= 10 N/m²
Size of surface imperfection k= 0.03 mm = 0.03 x 10³ m
Kinematic viscosity v = 1x10 m²/sec.
Density of water 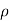 = 1000 kg/m³
= 1000 kg/m³
Step 1: Shear stress,
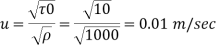
Step 2: Roughness Reynolds’s number,
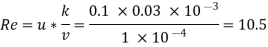
Re= 0.03 < 4
Since 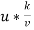 less than 4, between 4 and 100, and hence pipe Since surface behaves as smooth.
less than 4, between 4 and 100, and hence pipe Since surface behaves as smooth.
Q13) A pipe line carrying oil s= 0.8 has average height of irregularities projecting from the surface of the boundary of the pipe as 0.3 mm. What type of boundary is it? The shear stress developed is 3N/m². Take kinematic viscosity v = 0,012 stoke.
A13)
Given:
Average height of irregularities K = 0.3 mm = 0.3 x 10³ m
Shear stress =3 N/mm²
Specific gravity of oil s=0.8.
Density p=800 kg-m¹
Kinematic viscosity v=0.012 stoke=0.012x 10 m²/sec.
Step 1: Shear stress,
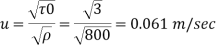
Step 2: Roughness Reynolds’s number,
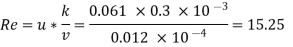
15.25> 4 but <100
The surface boundary is transition.
Q14) Air (p = 1.22 kg/m³ and v = 1.5 x 10 m³/s) flows through 250 mm diameter pipe at 8 m/s as mean velocity. If the equivalent sand grain roughness is 0.5 mm, calculate wall shear stress and friction factor f. Assume flow to be fully rough turbulent and neglect compressibility.
A14)
Given: p = 1.22 kg/m²
v = 1.5x 10³ m²/sec.
d = 250 mm = 0.25 m.
R= 0.125 m, u = 8 m/sec.,
K = 0.5 mm = 5 x 10¹ m
Step 1: Reynolds’s number
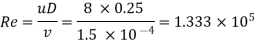
The flow is turbulent in the rough pipe.
Step 2: For rough turbulent pipe
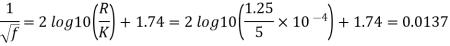
Step 3: Shear stress at the pipe surface
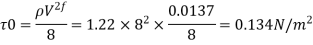
The wall shear stress is 0.134 N/m² and friction factor is 0.0137.
Q15) Determine the wall shearing stress in a pipe of diameter 100 mm which carries water. The velocities at the pipe centre and 30 mm from the pipe centre are 2 m/s and 1.5 m/s respectively. The flow in pipe is given as turbulent.
A15)
Given:
Diameter, D = 100 mm = 0.1 m,
Radius, R = 50 mm = 0.05 m
Velocity of centre, U = 2 m/sec
Velocity of 30 mm from centre u = 1.5 m/s,
y = 0.05-0.03 = 0.02 m
For turbulent flow,



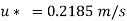
Wall shear stress,
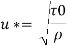
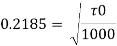
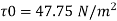
Q16) In a pipe of diameter 150 mm, carrying water the velocities at the pipe centre and 45 mm from pipe centre are found to be 2.5 m/s and 2 m/s respectively. Find the wall shearing stress.
A16)
Given: Diameter of pipe D = 150 mm = 0.15m,
:. Radius R = 0.15/2 = 0.075 m 2
Velocity of centre U=2.5 m/s,
Velocity at 45mm
U = 2 m/sec
At u = 2 m/sec, y = 0.075 -0.045 = 0.03 m
For turbulent Velocity
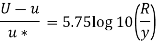
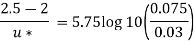
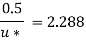
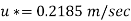
Shear stress,
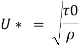
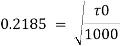
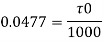

Q17) In a pipe of diameter 100 mm carrying water, the velocities at the pipe centre and 20 mm from the pipe centre are found to be 2.5 ms and 2.3 m/s respectively. Find the wall shear stress.
A17)
Given: D-100 mm-0.1m,
Radius R=005 m.
Velocity at centre U=2.5 m/s,
Velocity at 20 mm
u=2.3 m/s,
Velocity 2.3 m/s from pipe wall, y=0.05-0.02 -0.03m
For Turbulent flow
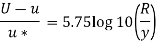
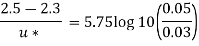
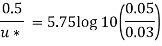
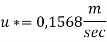
Shear stress
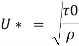
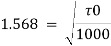
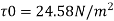
Q18) In a smooth pipe of diameter 0.5 m and length 900 m, water is flowing at a rate of 0.05 m/sec. Assuming kinematic viscosity of water as 0.02 stokes, find:
(1) Head lost due to friction
(2) Centre line velocity sub layer.
(3) Wall shear stress
(4) Thickness of laminar
Take friction factor f= 0.314/(Re)^(1/4) for turbulent.
A18)
Given:
d=0.5 m.
L=900 m. Q=0.05 m/sec.
V= 0.02 stokes.
Step 1: Mean velocity,
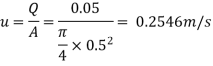
Step 2: Reynolds’s number,

Step 3: The flow is turbulent,

Step 4: Head loss by Darcy-Weisbach equation,
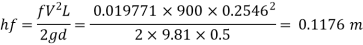
Step 5: Wall shear stress,
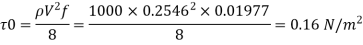
Step 6: Shear velocity.

Step 7: For turbulent flow in smooth pipe, maximum velocity is,
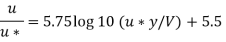
For y=-=0.25 m, v = (1.e. centre line viscosity)
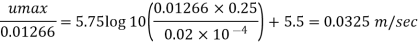
Step 8: Thickness of laminar sub-layer
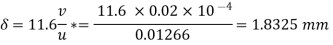
Q19) An oil with a kinematic viscosity 0.2 stoke and specific weight diameter is 30 cm and the discharge is 0.1 m/s. Determine 8000 N/m flows through a pipe. The pipe is smooth and its the maximum velocity through the pipe, thickness of the laminar sub layer, boundary shear stress and the velocity at the edge of the laminar sub layer.
A19)
Given: v= 0.2 stoke=0.2 x 10 m/Sec=8000 N/m,
D= 30cm=0.3 m, Q = 0.1 m'/Sec
To find: Umax, 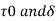
Mean velocity, u= Q/A =0.1/0236 = 0.4244 m/s
Reynolds number Re= ud/v= 0.4244x0.3/ 0.2x10
= 6366.19 >4000
As the Reynolds number is more than 4000, the flow is turbulent Friction factor by blasius equation
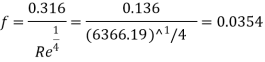
Shear velocity,

Maximum velocity for turbulent flow n smooth pipe is = 5.75 1080 (+55
for y = D/2=3=0.15m,
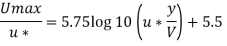
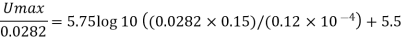
Thickness of laminar sub-layer
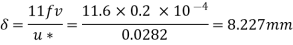
Velocity at the edge of laminar sub-layer, y = 8
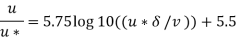
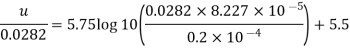
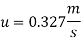
Q20) For turbulent flow through a pipe 60 cm in diameter, the velocities are 4.5 m/s and 4.2 m/s on the centre line and at a radial distance of 10 cm from pipe axis. Calculate the discharge in the pipe.
A20)
Given: D = 60 cm = 0.6 m, R = 0.3 m
Velocity at centre U=4.5 m/s.
Velocity at r=0.1 m, u = 4.2 m/s
Distance from wall surface y R-r-03-0.1-0.2 m
For turbulent flow
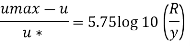
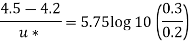
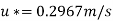
Relation between mean velocity and average velocity

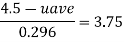
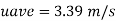
Discharge Q
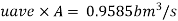
Q21) A fluid with specific gravity 1.1 and kinematic viscosity 1 x 10 m/s is to be pumped through a smooth pipe of diameter 300 mm over a length of 1 km. Flow rate is 4 m/min Calculate minimum pressure and power rating of the pump.
A21)
Given=
S= 11, v=1x10 m/h,
L= 1 km =1000 m
d = 300 mm = 0,3 m, Q = 4 m/min = 0.0667 m²/sec
Step 1: Velocity.
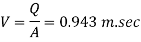
Step 2: Reynolds’s number,
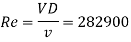
The flow is turbulent, Assume pipe is to be smooth.
Step 3: Nikuradse's empirical formula, when 10¹<R,<4x10'
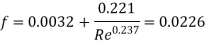
Step 4: Head loss due to friction,
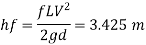
Step 5: Minimum pressure,
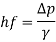
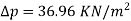
Step 6: Power rating of the pump,
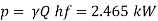
Q22) Two Pitot-Prandtl tubes are used to find the velocities at the middle and the quarter point of a circular pipe simultaneously. Find the discharge of water (Assuming turbulent flow)if the diameter of the pipe is 300 mm and readings of the tubes are 2.53 m/s and 2.29 m/s.
A22)
Given:
Diameter d = 300 mm = 0.3 m.
Velocity at middle u max=2.53 m/s at y = 0 Velocity at quarter Point of a circular pipe u = 2.29 m/s at y = 0.075
Step 1: Now for turbulent flow,
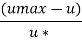
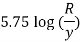
At y = 0.075
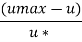
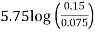 …(Eq.1)
…(Eq.1)
Step 2: At y=0 u. = 3.75,
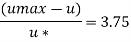
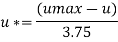
Put u* in equation 1
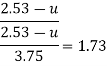
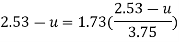
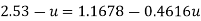
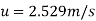
Step 3: Discharge.
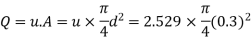
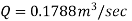
Q23) For turbulent flow in circular pipe of radius 'r friction factor is 0.02 Estimate the local velocity at a radial distance 0.25 r from the axis of the pipe. If mean velocity is 0.3 m/s, what will be the velocity at the centre line of pipe?
A23)
Given:
Radius R = r,
Frictional factor f=0.02,
Radial distance 10.25 r
Mean velocity u 0.3 m/s
Step 1: By Karman-Prandtl resistance equation for rough pipe is,
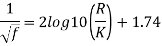
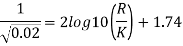
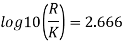
Step 2: Now using equation,
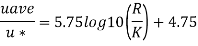
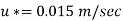
Step 3: Now for smooth and rough pipes,
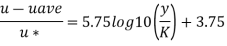
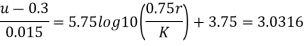
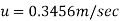
Step 4: Maximum velocity occurs at centre-line of pipe, r = 0, u = u max
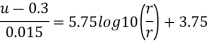
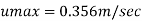
Local velocity at 0.25 r from axis of pipe is 0.3455 m /s and velocity at centre line is 0.356 m/sec.
Q24) A pipeline of 0.3 diameter carries liquid at the rate of 0.540 m/s. If the sp. gravity of the liquid is 0.80 and its kinematic viscosity is 0.023 x 10 m/s, determine the maximum permissible height of the protrusions up to which the pipe acts as smooth pipe and the height of the protrusions beyond which the pipe would become rough.
A24)
Given: d=0.3 m, Q=0.543 m/s
R= d/2 = 0.3 /2 = 0.15m
Average velocity of flow
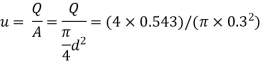
Reynold's number

Turbulent flow for smooth pipe for Re
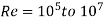
Relation for friction factor
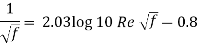
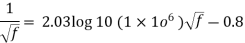

Solving above equation, we get f = 0.0113
Permissible height of the protrusions
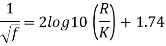
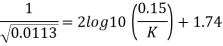
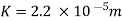
Q25) In a pipe of diameter 300 mm the centre line velocity and the velocity at a point 100 mm from the centre, as measured by pitot tube are 2.4 m/sec and 2 m/sec respectively, assuming the flow in the pipe to the turbulent find:
(1) Discharge through pipe
(2) Coefficient of friction
(3) Height of roughness projection.
A25)
Given:
Diameter d 300 mm=0.3 m,
Radius R 150 mm = 0.15 m
Velocity at centre u max = 2.4 m/sec.
Velocity at r=100=0.1 m;
u= 2 m/sec y=R-r=0.05 m
Step 1: Now for turbulent flow,
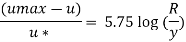
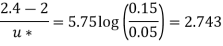
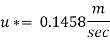
Step 2: The relation between velocity at any point and average velocity, at y R, u= u max
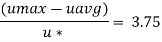


Step 3: Discharge,
Q = Area x Average velocity
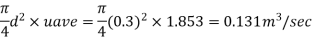
Step 4: Coefficient of friction,
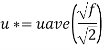
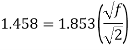
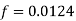
Step 5: Height of roughness projection, by using Karman-Prandtl resistance equation for rough pipe is, Use f4f (Friction factor f4 x Coefficient of friction)

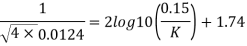
K=6.324 mm
Q26) Determine the head loss in kPa for a pipe line 700 m long carrying petrol at the flow rate of 200 Lps. (p = 730 kg/m³, μ = 2.92 x 10 N-s/m²). The diameter of the pipe is 30 cm and the equivalent roughness magnitude is 0.3 mm. Use Moody's diagram.
A26)
Given: L = 700 m long,
Q = 200 Lps= 0.2 m³/sec,
p = 730 kg/m³, μ = 2.92 x 10 N-s/m².
d = 30 cm = 0.3 m, e = 0.3 mm = 0.3 x 10³ m
Step 1: Velocity,
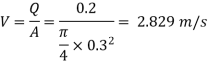
Step 2: Relative roughness,
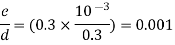
Step 3: Reynolds’s number,
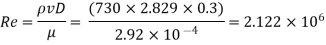
Step 4: Refer Moody's diagram and R., we get
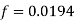
Step 5: Head loss by Darcy's equation,
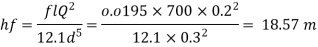
Step 6: Head loss in kPa (pressure),
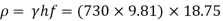
= 132.98 x 10³ mPa
p = 132.98 kPa
:. The head loss in kPa is 132.98 kPa.
Q27) Determine the head lost in a diameter 300 m, 300 m long cast iron pipe when (1) Water at 15°C flow at a velocity 15 nvs and (ii) Fuel oil at 15°C flow at the same velocity. Assume size of surface imperfection 0.244 mm. Refer Moody's diagram. Take the following properties.
Fluid | Density (kg/m^3 ) | Viscosity (m^2/s) |
Water | 999.1 | 1.141x10^-6 |
Fuel oil | 858 | 4.41x10^-6 |
A27)
Given:
L = 300 m, d = 300 mm = 0.3 m,
c = 0.244, V = 15 m/sec.
Case I: When water is flow with velocity = 15 m/sec.
e = 0.244
Step 1: Relative roughness
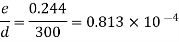
Step 2: Reynolds number
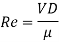
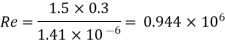
Step 3: Use moody's table for R. and values,
f = 0.0186
Step 4: Head loss by Darcy's equation,
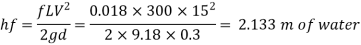
Case II: When oil flows with same velocity 1.5 m/sec,
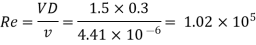
:. By using Moody's curve for Re and e/d values,
f = 0.0215
Head loss