Unit - 1
Simple Stresses and Strains
Q1) Explain the concept of stress and strain?
A1) 1. Stress
In mechanics, stress is defined as a force applied per unit area. It is given by the formula
σ=F/A
Where,
σ is the stress applied
F is the force applied
A is the area of force application
The unit of stress is N/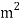
Stress applied to a material can be of two types. They are:
2. Strain:
According to the strain definition, it is defined as the amount of deformation experienced by the body in the direction of force applied, divided by initial dimensions of the body. The relation for deformation in terms of length of a solid is given below.
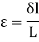
Where,
is the strain due to stress applied
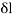is the change in length
L is the original length of the material.
The strain is a dimensionless quantity as it just defines the relative change in shape.
Depending on stress application, strain experienced in a body can be of two types.
Q2) Explain St. Venant’s Principal?
A2) Maximum principal strain theory is also known as St. Venant’s theory
This theory state as that the material subjected to complex stresses will fails when the maximum principal strain in it reaches the value of strain at yield point in a simple tensile test on materials
If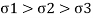 
are the principal stresses acting on three mutually perpendicular planes then maximum principal strain (e1) for no failure condition is given by,
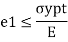
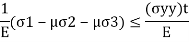
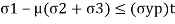where e1 must be positive and e3 must be negative
This equation shows the maximum principal strain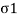 
may be greater than 
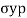which is unexpected condition in machine component so this theory is very little consideration
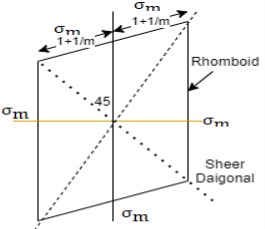
For two direction stress maximum principal strain theory is represented is shown in fig which is rhombus failure envelope.
Q3) Explain Stress and Strain Diagram?
A3) 1. Stress diagram
The internal resistance set up per unit cross sectional area is called as stress. It is denoted by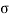 
In the equilibrium condition the internal resistance R is equal to an external load P
i.e., R=P
Where
P = load acting on the body
A = cross sectional area of the body
2. Strain Diagram:
Strain is simply a measure of deformation produced in a member due to the loads acting on it.
It is defined as the ratio of change in dimension to the original of the member
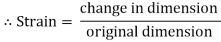
Q4) Define the term of Elasticity and plasticity
A4) 1. Elasticity:
It is property of a material by virtue of which its regions its original size and shape after deformation when the loads causing deformation are removed
2. Plasticity:
Lack of elasticity is called plasticity
The plasticity of a material is the ability to change its shape without destruction under the action of external load and to regain the shape given to it when the forces are removed.
Q5) What are the type of Stresses and Strain?
A5) 1. Stresses:
- Tensile Stress:
It is the force applied per unit area which results in the increase in length (or area) of a body. Objects under tensile stress become thinner and longer.
2. Compressive Stress:
It is the force applied per unit area which results in the decrease in length (or area) of a body. The object under compressive stress becomes thicker and shorter.
3. Shear stress:
When two equal opposite and parallel force acting tangential to the surface of the body is called as shear stress
2. Strains:
- Tensile Strain:
It is the change in length (or area) of a body due to the application of tensile stress.
2. Compressive Strain:
It is the change in length (or area) of a body due to the application of compressive stress
When we study solids and their mechanical properties, information regarding their elastic properties is most important. These can be obtained by studying the stress-strain relationships, under different loads, in these materials.
3. Shear strains:
The measure of small distortion of the block caused by the shear force is called shear strain
Q6) Explain Hooke’s Law?
A6) Hooke’s law
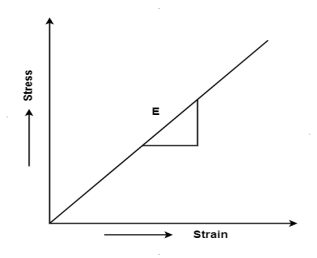
Hooke's law states that the strain of the material is proportional to the applied stress within the elastic limit of that material.
When the elastic materials are stretched, the atoms and molecules deform until stress is been applied and when the stress is removed, they return to their initial state
i.e., σ = E
Where,
σ is the stress
E is the modulus of elasticity also known as Young’s modulus
ε is the strain
When the stress is removed from the material, there are two types of deformation that can take place: plastic deformation and elastic deformation
Q7) What is Stress- Strain Diagram for Mild Steel?
A7) Stress-Strain Diagram for mild steel (ductile material)
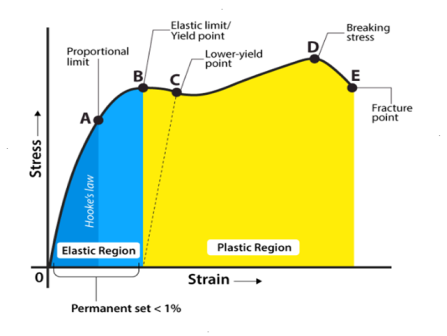
Explaining Stress-Strain Graph
The stress-strain graph has different points or regions as follows:
Proportional limit
Elastic limit
Yield point
Ultimate stress point
Fracture or breaking point
(i) Proportional Limit
It is the region in the stress-strain curve that obeys Hooke’s Law. In this limit, the ratio of stress with strain gives us proportionality constant known as young’s modulus. The point OA in the graph is called the proportional limit.
(ii) Elastic Limit
It is the point in the graph up to which the material returns to its original position when the load acting on it is completely removed. Beyond this limit, the material doesn’t return to its original position and a plastic deformation starts to appear in it.
(iii) Yield Point
The yield point is defined as the point at which the material starts to deform plastically. After the yield point is passed, permanent plastic deformation occurs. There are two yield points (i) upper yield point (ii) lower yield point.
(iv) Ultimate Stress Point
It is a point that represents the maximum stress that a material can endure before failure. Beyond this point, failure occurs.
(v) Fracture or Breaking Point
It is the point in the stress-strain curve at which the failure of the material takes place.
Q8) What do you mean by working stress and factor of safety?
A8) Working Stress
It is defined as the ratio of the actual axial load and the original cross-sectional area of the specimen.
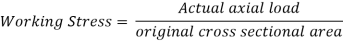
Working stress is the maximum allowable stress to which a material is subjected during its service load
For a safety of a structure, it is very essential that the working stress should be within the elastic limit of the material
Factor of Safety
The ratio of the ultimate stress to the working stress for a brittle material is called factor of safety.
The ratio of the yield stress to the working stress for a ductile material is called factor of safety
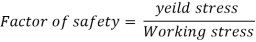
In designing to resist accidental loads sufficient reserve strength is required to be ensured which is called out by taking a suitable factor is called as factor of safety
Q9) What do you mean by lateral strain and Poisson’s ratio?
A9) Lateral Strain
Strain in the direction at right angles to the direction of applied force is known as lateral strain.
It is the ratio of change on lateral dimension to the original lateral dimension of the member.
Lateral strain =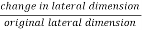 
For rectangular bar
Lateral strain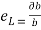 
or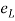
= 
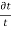
Poisson’s Ratio
When a body is subjected to simple tensile stress within its elastic limits then there is a change in the dimensions of the body in the direction of the load as well as in the opposite direction.
When these changed dimensions are divided with their original dimensions, longitudinal strain and lateral strain are obtained.
The ratio of the lateral strain to the longitudinal strain is called Poisson’s ratio.
It is represented by the symbol “µ”. Poisson’s ratio is maximum for an ideal elastic incompressible material and its value is 0.5.
For most of the engineering materials, Poisson’s ratio lies between 0.25 and 0.33. It has no units.
Q10) Explain volumetric strain?
A10) Volumetric Strain
When a body is subjected to external forces on its face, there will be a change in its volume
The Ratio of change in volume to the original volume is known as volumetric strain
It is denoted by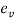 
.
Where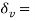 
change in volume and
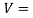original volume
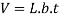
By partial differentiation
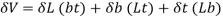
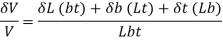
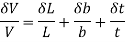
i.e.,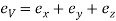 
Volumetric Strain is the algebraic sum of all axial or linear strains
i.e.,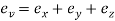 
Where,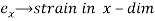 
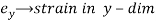
Q11) What are the Elastic Moduli and the relationship between them?
A11) Different elastic constants are as follows:
- Young’s modulus
- Bulk modulus
- Rigidity modulus
- Poisson’s ratio
1. Young’s Modulus
According to Hooke’s law, when a body is subjected to tensile stress or compressive stress, the stress applied is directly proportional to the strain within the elastic limits of that body. The ratio of applied stress to the strain is constant and is known as Young’s modulus or modulus of elasticity.
Young’s modulus is denoted by letter “E”. The unit of modulus of elasticity is the same as the unit of stress which is megapascal (Mpa).
1 Mpa is equal to 1 N/mm2.
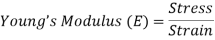
Fig: Body Subjected to Tensile Stress
2. Bulk Modulus
When a body is subjected to mutually perpendicular direct stresses which are alike and equal, within its elastic limits, the ratio of direct stress to the corresponding volumetric strain is found to be constant.
This ratio is called bulk modulus and is represented by letter “K”.
Unit of Bulk modulus is Mpa.
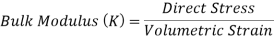
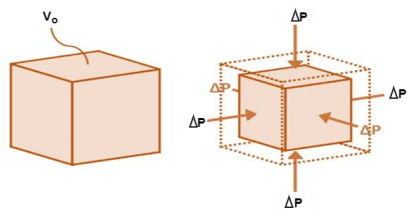
Fig: Volumetric Change of Body
3. Rigidity Modulus
When a body is subjected to shear stress the shape of the body gets changed, the ratio of shear stress to the corresponding shear strain is called rigidity modulus or modulus of rigidity.
It is denoted by the letter’s “G” or “C” or “N”.
Unit of rigidity modulus is Mpa.
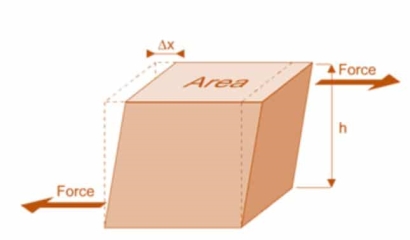
Fig: Shear Deformation of Body
4. Poisson’s Ratio
When a body is subjected to simple tensile stress within its elastic limits then there is a change in the dimensions of the body in the direction of the load as well as in the opposite direction.
When these changed dimensions are divided with their original dimensions, longitudinal strain and lateral strain are obtained.
The ratio of the lateral strain to the longitudinal strain is called Poisson’s ratio.
It is represented by the symbol “µ”. Poisson’s ratio is maximum for an ideal elastic incompressible material and its value is 0.5.
For most of the engineering materials, Poisson’s ratio lies between 0.25 and 0.33. It has no units.
5. Relationship between Elastic Constants
- The relationship between Young’s modulus (E), rigidity modulus (G) and Poisson’s ratio (µ) is expressed as:
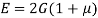
- The relationship between Young’s modulus (E), bulk modulus (K) and Poisson’s ratio (µ) is expressed as:
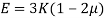
- Young’s modulus can be expressed in terms of bulk modulus (K) and rigidity modulus (G) as:
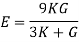
- Poisson’s ratio can be expressed in terms of bulk modulus (K) and rigidity modulus (G) as:
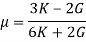
Q12) What is bars of varying section- composite bar?
A12) A composite bar product of bars of various substances rigidly constant collectively in order that each bars strain collectively below outside load.
Since traces within side the bars are same, the stresses within side the bars rely on their Young’s modulus of elasticity. In different words, a stiffer bar will proportion predominant element of outside load.
In a composite machine the 2 bars of one-of-a-kind substances aren't joined collectively, however they assist a 0.33 inflexible bar.
Load utility at the 0.33 inflexible bar is such that extrude in period of each bar is the same, generating one-of-a-kind stresses in bars.
A meeting of bars, located co-axially, however having one-of-a-kind lengths.
Bar of Varying Sections. The strain and deformation of duration prompted in every of the sections of the bar are different, even though the axial load performing at the bar is the same.
The derivation is accompanied with the aid of using the precept that, Total Change in duration, dL = Sum of Change in duration of Section 1, Section 2 and Section 3.
A composite bar fabricated from two bars of various substances rigidly constant collectively in order that both bars stress collectively be neat outside load.
In a composite gadget the two bars of various substances aren't joined collectively, however they assist a 3rd rigid bar.
The quantity of any square solid, together with a cube, is the area of its base (period instances width) accelerated with the aid of using its height: V = l × w × h. Therefore, if a pass section is parallel to the pinnacle or backside of the solid, the area of the pass-section is l × w
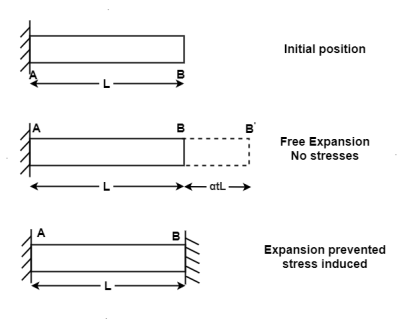
Q13) Explain temperature stresses?
A13) Temperature Stresses
When the expansion or Contraction of the member due to temperature variation is prevented the stresses induced in the member is called Temperature stresses
When the Temp is rise, the stresses induced in the member are compressive in nature.
When Temp falls, the stresses induced are Tensile in nature
We know,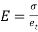 
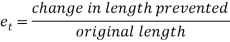
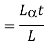
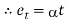
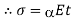
Where, = Coefficient of thermal expansion in 1
C or 1
k
T = Temperature Variation in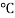 
or K.
E = Young’s Modulus,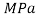
Q14) What do you mean by strain energy, resilience, Gradual, Sudden, Impact and Shock Loading – Simple application
A14) 1. Strain energy
When a load is applied on an elastic body it gets deformed i.e., the work is done by the load on the body
This work done is stored in a body is called as strain energy or resilience
When the load is removed the body regains to its original position because of stored energy
It can be easily visualized in springs when the springs is loaded it gets compressed and regain to its original position immediately when the load is removed
The amount of the strain energy stored in a body is depended on the type of loading i.e., axial load, bending load, shear load and torsion load etc.
2. Resilience:
The energy which is stored in a body within an elastic limit is called a strain energy or resilience it is denoted by U
3. Stress due to gradually applied load:
When a body is subjected to the gradually applied load, the stress increases from zero to the maximum value gradually
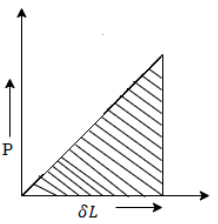
Let p= gradually applied load
L = Extension due to load
= maximum stress induced in the member
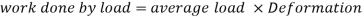
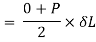
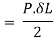
Strain energy stored in body
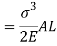
But Work done = Strain Energy stored
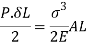
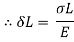
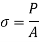
4. Stress due to suddenly applied load
When the load acting on a body is sudden the body gets deformed immediately after applying load for e.g., Weight of truck enter on weighing machine is an example of sudden load
Let P= suddenly applied load
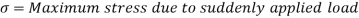
Work done by load = Area under curve
= P.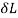 
Strain energy stored in a body =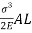 
But work done = strain energy stored
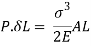
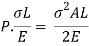
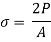
Stress due to sudden load is twice the stress due to gradually applied load.
4. Stresses due to Impact load
When a load applied on a body is falls from a certain height is called as impact or falling load
Consider a member is fixed at its top and a collar is attached to its lower end as shown in fig.
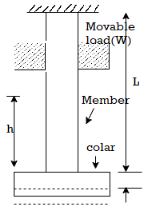
Let, W= weight of movable load
H = height of fall
L= length of member
A = cross sectional area
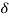L: = Deformation of length
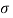= Instateneous stress
Work done by external movable load = W (h+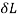
)
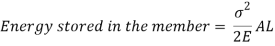
But work done by load = Energy Stored in member
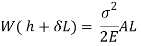
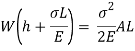
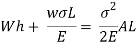
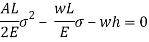
Multiplying both numerator and denominator by E/2E we get,
Maximum instantaneous stress
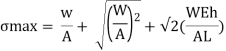
But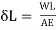 
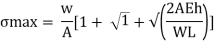
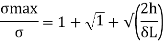
The dimensionless ratio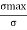 
is called as load factor and it is denoted by n
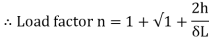
5. Shock loading – simple application
Shock loading:
Shock loading present sainted resting set of problems to the designed engineer. In the engineering com-munity, layout for static loading traditionally has been the maximum commonly used design procedure.
Designing for surprise loading, however, requires change of thinking in ever all areas.
The objectives of this discussion are to introduce the simple principles of surprise loading and to consider their effect upon the intently of structure
Static loading happens whilst a pressure is slowly applied to a member.
This is a gradual or constant loading system this is equivalent to loading them ember over a length of 1min.
Designing for static loading traditionally has been the method used for an extensive type of components, inclusive of buildings, water towers, dams.
Fatigue loading happens whilst the member stories alternating, repeated, or fluctuating stresses.
Fatigue loading generally is classified through the number of loading cycles at the member and the stress level.
Q15) A rectangular bar of steel 50 mm× 30mm is 1m long carries a pull of 93.9KN, find tensile stress in the bar, strain and change in length, Take E=200 GPa
A15) Given:
P=93.9 KN=93.9×103 N
b=50mm
t=30mm
L=1m=1000mm
E=200GPa=200×103 MPa
Tensile stress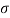 
= P/A =
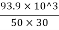= 62.6MPa
Tensile strain, E= σ/e
∴ e = σ/E =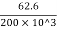 
=3.13 ×10-4
Change in length e=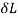
/L
∴ δL = eL =3.13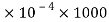
=0.313 mm
Alternative δL =
= 
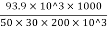=0.313mm
Q16) A copper wire of length 600 mm is subjected to an axial pull of 10 KN. Find the minimum diameter so that stress is not to exceed 75 MPa. Also calculate the elongation of E=100 GPa.
A16) Given:
P=10KN=10×10^3N
L=600mm
E= 100GPa = 100×10^3 MPa
Diameter of wire ‘d’ and elongation δL
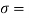P/A
∴75=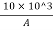
A=133.33 mm2
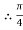d^2 = 133.33
∴d = 13.03 mm
Elongation δL =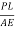
=
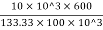=0.45 mm
Q17) Determine the value of safe axial pull for the rectangular bar as shown in fig. Thickness of bar is 15 mm throughout. Tensile stress in the bar should not exceed 120MPa.
A17) Given: 
= should not be more than 120MPa
Maximum stresses induced at the section having smaller cross sectional area.
Consider section 1-1 cutting first part of hole and 2-2 at second part
Area at 1-1 A1 =(b-d) t = (100-60) ×15 = 600 mm2
Area at 2-2 A2 =80×15=1200mm2
∴Least cross sectional area A = 600 mm2
∴ Safe load P= σ × A=120×600=72000N=72KN
Q18) A bar of cross-section 8mm×8mm is subjected axial pull of 10kN. The lateral dimensions of the bar are found to be reduced by 2×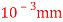
. Find Poisson’s ratio and modulus of elasticity assuming 
A18) Given:
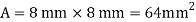
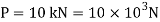
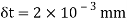
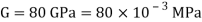
To find: and E
Lateral strain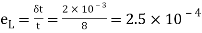 
Lateral strain 
Stress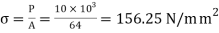 
Modulus elasticity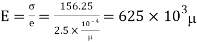 
Using relation
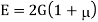
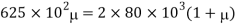
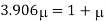
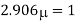
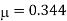
Q19) A bar of 25mm diameter, is objected to a pull of 40kN. The measured extension on gauge length of 200 mm is 0,085 mm and change in diameter is 0.003 mm. Calculate the Poisson’s ratio and the three values of the module.
A19) Given:
To find and K
Area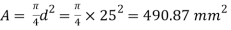 
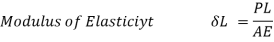
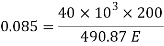
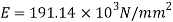
Poisson’s ratio 
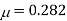
Young’s modulus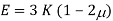 
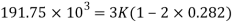
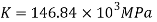
Shear modulus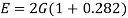 
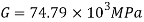
Q20) A 50mm square steel bar is subjected to an axial tensile load of 250 kN. Determine the decrease in the lateral dimension if E=200 GPa and v=0.30.
A20) Given:
Side a=50mmP=250kN=250×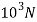
,=0.3
E=200 GPa=200×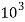
MPa
To find: δa
Stress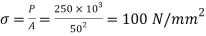 
Linear strain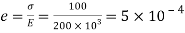 
Change in lateral dimension
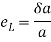
Q21) A bar of diameter 20 mm and length 200, extends by a length of 0.4 mm upon application of a load P. What is the value of P if the young’s modulus of the material is known to be 2×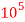
N/m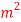
. What is the change in the cross sectional area of the bar at this stage if the Poisson’s ratio is 0.28. If an extension of the bar were to be limited to 0.3mm under same load P, what should be the diameter of the bar?
A21) Given:
To find
(i) P for δL =0.4(ii) P for δL =0.28 (iii) Diameter d for δL =0.3
Case I: Applied load P for δL=0.4mm
Given d=20mm L=200mmδL=-.4mmE=2×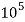
N/m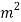
Area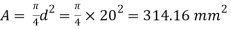 
Axial load P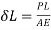 
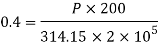
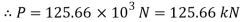
Case II: Change in cross-secitonal are if =0.28
Linear strain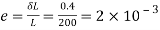
Lateral strain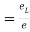 
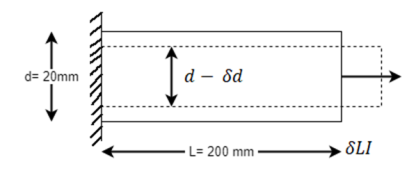
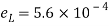
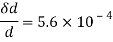
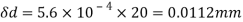
Reduced diameter 
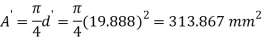
Case III: Diameter of the bar if δL=0.3mm
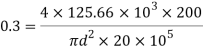
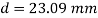
Q22) A circular rod of 120 mm diameter and 500 mm long is subjected to a tensile load of 1000kN. Determine Modulus of Rigidity, Bulk Modulus and change in volume. Assume Poisson’s ratio 0.3 and 
A22) Given:
Diameter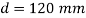
Length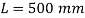
Tensile load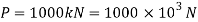
Poisson’s Ratio = 0.3
Modulus of Elasticity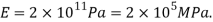 
To find: G, K, dv
Using relation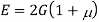 
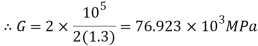
Now,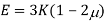 
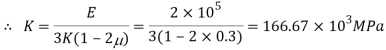
Change in Volume
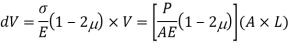
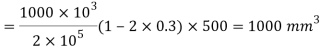
Q23) A cylindrical piece of steel 80 mm diameter and 120 mm long compressive force 70kN. Calculate the change in volume of the piece if Bulk modulus is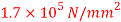 
and Poisson’s ratio is 0.3.
A23) Given:
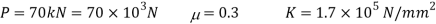
To find: δV
Modulus of elasticity
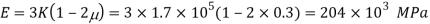
Area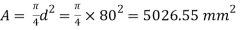 
Stress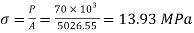 
Volumetric strain for member subjected uniaxial force
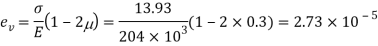
Q24) A steel rod, 40 mm diameter and 5 m in length is suddenly subjected to an axial pull of 50 KN. Determine-
1) The work done and
2) Maximum and instantaneous elongation
A24) Assume E = 2×10^5 MPa
Given:
D=40 mm
L=5m=5000 mm
P=50 KN =50×10^3 N(suddenly)
E= 2×10^5 MPa
1) Workdone=?
Area A =
402 =1256.6 mm2
Workdone = strain energy
U =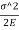
volume
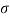instantaneous stress = 2P/A =
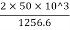= 79.58 MPa
U =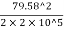 
(1256.6×5000)
=99.47×10^3 N.m=99.47 J
2) Instantaneous elongation
= 
=
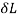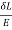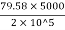=1.9895 = 2mm
Q25) A solid vertical prismatic steel bar of equilateral triangle section of side 20 mm is firmly fixed at the top. A rigid collar at a distance of 600 mm from the top. Calculate the strain energy stored in each of the following case:
a) when pull of 10KN applied gradually.
b) when a force of 8 KN is suddenly applied.
c) when a weight of a 4KN falls through 120 mm before it strikes the collar.
Take E= 200 GPa
A25) Given:
Side of triangle b=20mm
Length of bar L=600mmm
E= 200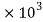
MPa
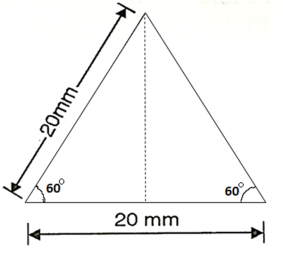
Fig.: Cross section of Bar
To find:
(a) U, when P=10kN gradual
(b) U, when P=4kN sudden and
(c) U, when P=8kN falls through 120mm
Area of cross section A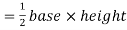 
Case (a):
When pull 10kN is gradually applied
Stress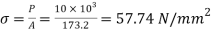 
Strain energy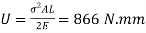 
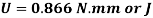
Case (b):
When a weight of 8kN falls through 120mm
Stress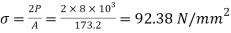 
Strain energy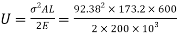 
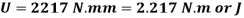
Case(c):
When a weight of 4kN falls through 120mm
Stress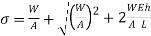 
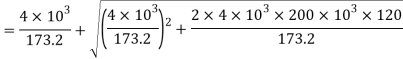
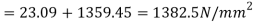
Strain energy 
Q26) Determine the instantaneous stress and deformation of a rod length 1 m and diameter 6 mm, if a mass of 50kg falls through a height of 10cm and strikes the bottom of the rod. The rod is freely suspended and fixed at the top. Assume E=210 GPa.
A26) Given 
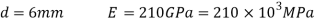
To find:
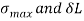
Weight W=mg=50×9.81=490.5 N
Area of rod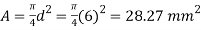 
Instantaneous stress
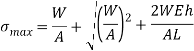
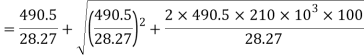
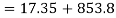
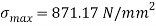
Deformation of rod
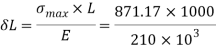
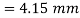
Q27) A 2m long alloy bar of 150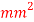 
cross sectional area hangs vertically and has a collar securely fixed at tis lower end. Find the stress induced in the bar, when a weight 2kN falls from a height of 100mm on the collar. Take E=120 GPa. Also find the strain energy stored in the bar.
A27) Given:
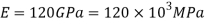
To find: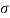 
and U
Instantaneous Stress
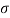
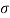
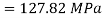
Strain Energy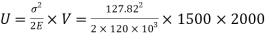 
Q28) A load of 500 N falls freely through a height of 150mm on to a collar attached to the end of a vertical rod of 50 mm diameter and 2m long, the upper end of the rod being fixed to ceiling. Calculate the maximum instantaneous extension of bar. Also calculate the maximum stress in the bar. Assume E=200GPa
A28) Given: W=500N d=50mm
h=150mm,L=2 m=2000mm
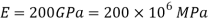
To find:
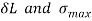
Area 
Instantaneous stress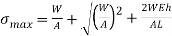 
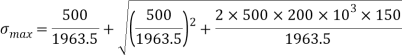
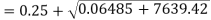
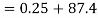
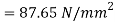Maximum instantaneous elongation
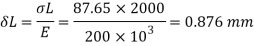
Q29) An unknown weight falls through 10mm on a collar rigidly attacked t the lower vertical bar 3m long and 600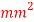 
in section. If the maximum instantaneous extension is 2mm, what is the corresponding stress and the value of unknown weight? Take E=200 GPa
A29) Given:
Height of fall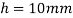 
Length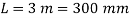 
Area 
Extension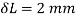 
Young’s modulus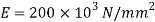 
To find: Instantaneous stress and weight W
Maximum Instantaneous stress,
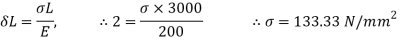
Work done by falling load = Energy stored
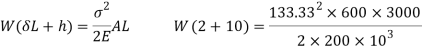
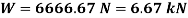
Alternative method,
Let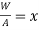 
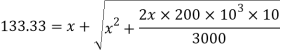
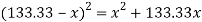
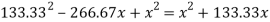
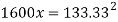
But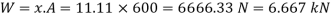 
Q30) A weight 2kN is dropped onto a collar at the lower end of a vertical bar 3m long and 28mm in diameter. Calculate the maximum height of drop if the maximum instantaneous stress is not to exceed 140 MPa. What is the corresponding instantaneous elongation? Also Find the dynamic force at instant of maximum elongation?
A30) Given 
To find h and δL
Area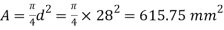 
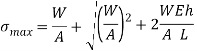
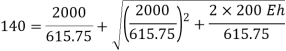
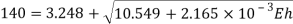
Squaring both side
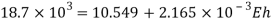
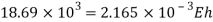
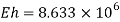
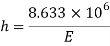
Instantaneous elongation
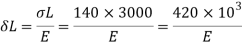
Q31) A vertical steel bar 15mm diameter, 1.4m long is provided with a collar at lower end. Find the maximum weight W that can be dropped through a height a height of 95mm over the collar, if maximum permissible tensile stress is 150 MPa. Use E=200GPa.
A31) Given:
Diameter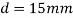
Long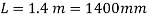
Height of fall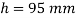 
Maximum stress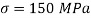
Young’s modulus
Area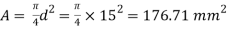
To find: Weight W,
Instantaneous stress,
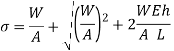
Let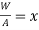 
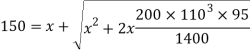
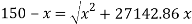
Squaring both side,
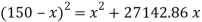
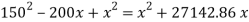
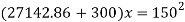
But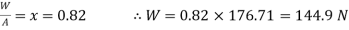 
The maximum weight that can be applied on collar is 144.9 N.
Q32) Fig. Shows a wire suspended from top with a disc attached at bottom. Calculate the height h from which the load of 2 N can be permitted to fall on the disc, so that maximum stress in the wire does not exceed 150 N/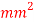
. Take modulus of elasticity for the material of the wire as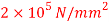 
A32) Given
Weight
Area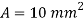 
Length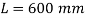 
Maximum stress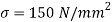
Modulus of elasticity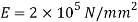 
To find:
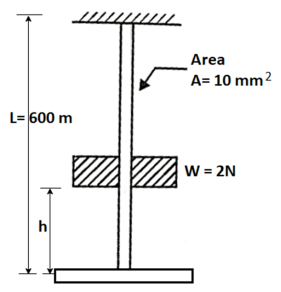
Height of fall h
Instantaneous stress for impact load,
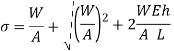
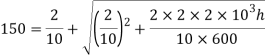
Squaring both side,
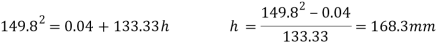
The load is fall from a height of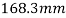 
Q33) A load of 50 N falls by gravity through a vertical distance of 2000mm. When it is suddenly stopped by a collar at the end of a vertical rod of length 6m and diameter 20mm, calculate the maximum stress and strain induced in the bar. The top of the bar is rigidly fixed to ceiling. Assume 
A33) Given:
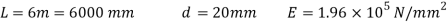
To find: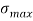 
and e
Area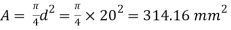 
Maximum Instantaneous stress,
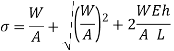
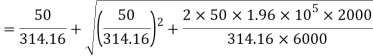
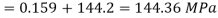
Instantaneous deformation
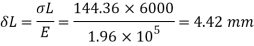
Strain e=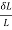
=4.42/6000=7.365×10^-4
