Unit - 3
Second Law of Thermodynamics
Q1) A Reverse Carnot cycle for refrigeration absorbs heat at 270K and rejects at 300K. Calculate the Coefficient of performance of this cycle. If the cycle is absorbing 1130kj/min at 270 K How many kJ work is required per second?
A1)
T1 = 270 K and T2 = 300 K
As we know that
C.O.P = T1/ T2 – T1
C.O.P = 270 / 300 – 270
C.O.P = 9
Work Require per second
Heat absorbed at 270 K,
Q1 = 1130 kJ/min = 18.83 kJ/s.
As we have discussed above
C.O.P = Heat Absorbed / Work Done
9 = 18.83 / Work Done
Work Done = 2.1 kJ / s
Q2) Explain Energy transfer by heat, work, and mass
A1)
1. Heat transfer (Q)
Heat transfer is the energy interaction caused by a temperature difference between a system and its surroundings. Heat transfer to a system (heat gain) will cause the internal energy of the system to increase, and heat transfer from a system (heat loss) will cause the internal energy of the system to decrease
2. Work (W)
The energy interaction that is not caused by a temperature difference between a system and its surroundings is work. Work transferred to a system will increase the energy of the system, and work transferred from a system will decrease the energy of the system.
3. Mass flow
When mass enters a system, the energy of the system increases because of the energy accompanied by mass. Also the energy of the system decreases when mass leaves the system Heat and work have been introduced in the previous sections. Systems that involve energy balance with mass flow are considered in the following section.
Q3) Write Isentropic Efficiencies of Turbines?
A3)
The ratio of the actual work output of the turbine to the work output that would be achieved if the process between the inlet state and the exit pressure were isentropic
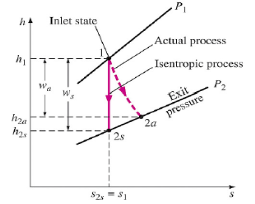
Fig 1
η = Actual turbine work / Isentropic turbine work = wa/ws
h1 - h2a / h1-h2s
∆ke<<∆h
∆pe<<∆h
Q4) Find Isentropic Efficiencies of Compressors and Pumps?
A4)
The ratio of the work input required to raise the pressure of a gas to a specified value in an isentropic manner to the actual work input
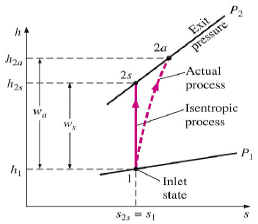
Fig 2

A realistic model process for compressors that are intentionally cooled during the compression process is the reversible isothermal process, defined as isothermal
Efficiency
c = wt / wa
Q5) Write Isentropic Efficiencies of Nozzles?
A5)
The ratio of the actual kinetic energy of the fluid at the nozzle exit to the kinetic energy value at the exit of an isentropic nozzle of the same inlet state and exit pressure

Fig 3
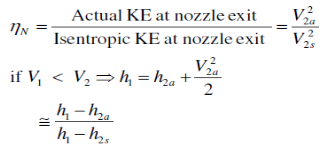
Q6) Discuss Entropy Balance?
A6)
Increase of entropy principle for any system
(Total entropy entering) – (total entropy leaving) + (total entropy generated) = (change in the total entropy of the system)
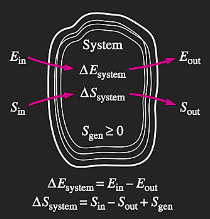
Fig 4
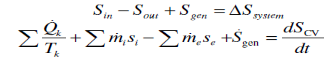
The entropy change of a system during a process is equal to the net entropy transfer through the system boundary and the entropy generated within the system
Entropy change of the system

Q7) Discuss Isentropic Process?
A7)
An isentropic process is a thermodynamic process, in which the entropy of the fluid or gas remains constant. It means the isentropic process is a special case of an adiabatic process in which there is no transfer of heat or matter. It is a reversible adiabatic process. An isentropic process can also be called a constant entropy process. In engineering such an idealized process is very useful for comparison with real processes.
Since there are changes in internal energy (dU) and changes in system volume (∆V), engineers often use the enthalpy of the system, which is defined as:
H = U + pV
In many thermodynamic analyses it is convenient to use the enthalpy instead of the internal energy. Especially in case of the first law of thermodynamics
Q8) Discuss Saturated Mixture?
A8)
During the vaporization process of water, the substance is a mixture of saturated liquid and saturated vapor. Quality (x) is defined to describe the fraction of saturated vapor in the mixture.
x = mvapor/mtotal
where
mvapor = mass of vapor in the mixture
mtotal = total mass of the mixture
mtotal = mliquid + mvapor = mf + mg
Quality has a value between 0 and 1. x equals 1 for saturated vapor and x equals 0 for saturated liquid according to its definition.
Saturated mixture is a two-phase system. For convenience, it can be treated as a homogenous mixture and the properties of this mixture are simply the average properties of the saturated liquid and saturated vapor. For example, the specific volume of the mixture can be determined by
Vav = Vf + Vg
mtotal vav = mf vf + mg vg
vav = mf vf/mtotal + mg vg/mtotal
= vf (1 - mg/mtotal) + vg mg/mtotal
= vf (1 - x) + vg x
= vf + vfg x
Rearranging the above equation to give an expression for the quality x as
x = (vav - vf)/vfg
Based on this equation, quality can be determined from the horizontal distance on the T-v or P-v diagram as shown in the figure.
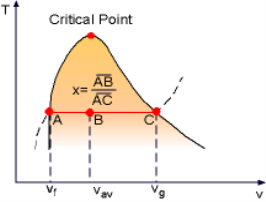
Fig 5 Quality is related to the horizontal distance on T-v diagram
The above process can be repeated for u and h
uav = uf + ufg x
hav = hf + hfg x
Q9) Superheated Vapor
A9)
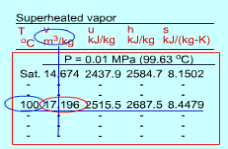
Fig 6 Superheated Water Table
Since the superheated vapor is a single phase substance, the temperature and pressure are independent. In the superheated vapor tables, the properties are listed as a function of both the temperature and pressure. The tabulated properties include v, u, h and s. The saturation temperature corresponding to the pressure is given in the parentheses following the pressure value.
Superheated vapor can be characterized by
- P < Psat at a given T
- T > Tsat at a given P
- v > vg at a given P or T
- u > ug at a given P or T
h > hg at a given P or T
Q10) Discuss Sub cooled Liquid?
A10)

Fig 7 Sub cooled Water Table
The format of the sub cooled liquid water tables is similar to the format of the superheated vapor tables. In the absence of compressed liquid data, a common practice is to use the saturated liquid data based on the given temperature to estimate the properties of compressed liquid. For h, the error can be reduced using the following approximation
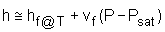
Sub cooled liquid can be characterized by
- P > Psat at a given T
- T < Tsat at a given P
- v < vf at a given P or T
- u < uf at a given P or T
h < hf at a given P or T
The entropy of a pure substance is determined from tables in the same manner as other properties such as v, u, and h. The value of entropy at a specified state is determined just like any other property.
- Compressed liquid: from tables
- Saturated liquid (sf): from tables
- Saturated mixture: s = sf + xsfg
where
x = quality
sfg = sg - sf - Saturated vapor (sg): from tables
- Superheated vapor: from tables
If the compressed liquid data are not available, the entropy of the compressed liquid can be approximated by the saturated liquid at the same temperature