Unit - 2

Soil Hydraulics

Q1) What are the stress conditions in soil?

A1)

• Consider a rigid cylindrical mould or container as shown in Fig. The dry sand is filled in this rigid cylindrical mould. It is assumed that there is no side friction in the cylindrical container or mould.

• Surface of the soil is subjected to load Q through a piston and this load is transferred to the dry soil grains filled in the container through their points of contact. The average stress at any section x-x can be determined as follows

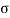av =

Where, 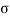av =Average stress; A= sectional area of the cylinder

Any plane like x-x do not pass through all the points of contact, but many of the grains are cut by the plane x-x and the actual points of contacts seems like a wavy form.

The average stress which is responsible for the deformation of the soil mass is called as effective stress or intergranular stress see Fig. For better understanding. Note that o, o is the effective stress.

• In another experiment, cylindrical mould is filled with the fully saturated soil and cylindrical mould is entirely made water tight. If the same load (Q) is placed on the piston, the load will not be transmitted to the soil grains but in case of Fig. The same load was transmitted to the soil grains (dry).
• Pore Pressure: The pressure which is developed in the water due to external load transmitted to the water in the pore by assuming water to be incompressible is called as pore pressure or neutral stress (uw) which is shown in Fig.

Fig.: Specimen

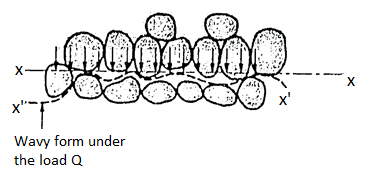
Fig.: Intergranular pressure

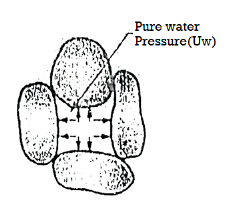
Fig.: Pore water pressure

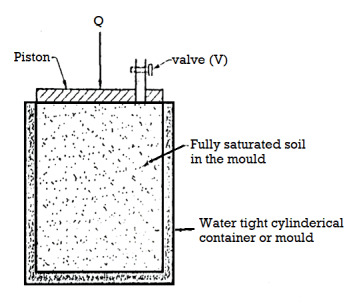
Fig.: The effective stress principle

Fig.: The effective stress principle

uw = neutral stress=Q/A

Where, Q=load applied by piston

A=sectional area of the cylinder

Uw =pore pressure or neutral stress

• In Fig., as soon as valve V is opened, there will be immediately, expulsion of water through the hole and this flow continues for some time and then stops. Note that expulsion of water from the pores decreases the pore water pressure, but increases the intergranular pressure. Hence at any stage; the total pressure split up between water and the points of contact of grains which make a new equation as follows:

Total pressure () = 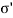+ uw

Where, 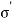=Intergranular pressure

Uw =pore water pressure or neutral stress.

For no expulsion of water, uw = 0,

Hence total pressure (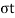)= Intergranular pressure ()

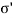Fig. Shows the concept of total pressure, intergranular pressure and pore water pressure.

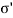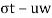• = is called as effective stress equation where 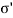=effective stress, 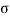t=total pressure and uw= pore water pressure.

Q2) What are the factors affecting permeability?

A2)

Permeability depends on many factors. Following are the main factors that affect permeability:

Grain size:

• Grain size of the soil, or the effective size Dio is one of the factors which affect permeability. Allen Hazen gave the relation.

K = C(D10)2

Where, K Coefficient of permeability in cm/s and D10 is the effective grain size of the soil, C= constant (between 100 to 150)

• The permeability of coarse-grained soil is more than that of fine-grained soil

Properties of pore fluid:

• Permeability is directly proportional to the unit weight of pore fluid and inversely proportional to the viscosity of the pore fluid.

Temperature:

• Since viscosity of the pore fluid decreases with the temperature, permeability increases with temperature, as unit weight of the pore fluid does not change much with change in temperature.

Void ratio:

• Increase in void ratio increases the area available for flow, hence the permeability increases for critical conditions.

K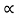e2

Stratification of soil:

• Stratified soils are those, which are formed by layer upon layer of earth or dust deposited upon one another.
• If the flow is parallel to the layers or stratification, the permeability is maximum while the flow in perpendicular direction to the stratification occurs with minimum permeability.

Entrapped air and organic impurities:

• Organic impurities and entrapped air obstruct the flow and coefficient of permeability is reduced due to their presence.

Adsorbed water:

• Adsorbed water means a thin, microscopic film of water surrounding individual soil grains.
• This water is not free to move and hence reduces the effective pore space and thus decreases the coefficient of permeability.

Degree of saturation:

• The permeability of partially saturated soil is less than that of fully saturated soil.

Shape of particles:

• Permeability is inversely proportional to the specific surface e.g., the angular particles have more specific surface as compare to rounded particles. Therefore, the soil having angular particles is less permeable than soil of rounded particles.

Structure of soil mass:

• For same void ratio the permeability is more for flocculant structure as compare dispended structure.

Q3) Explain Constant head method as per IS2720?

A3)

• It is based on measuring the volume of water flowing through a soil sample of known cross sectional area A and length L in time t under a constant head h of water.
• The arrangement is shown in Fig.

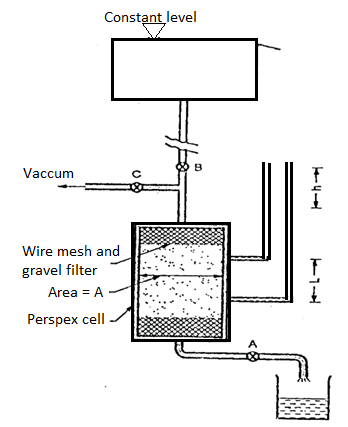
Fig.: Constant head permeability test

• The soil sample is enclosed in a Perspex cylindrical tube. A number of manometer points are provided of the side of the cylinder. These can be used in pairs.
• One such pair is shown in the figure.
• Water is allowed to flow through the soil at a constant head 'h' as indicated by the level difference in manometer tubes.
• The quantity of water or volume of water V collected in time t is measured, from which discharge q is calculated. The coefficient of permeability is then calculated as,

K= =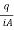

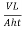
Where q=v/t=discharge in m3/s

V=volume of water collected in m3 in time t sec

A=cross sectional area of specimen in m

h =level difference between the manometer tubes in m.

L =distance between manometer points in m

• Vacuum is used at the start of the test to ensure that all entrapped air from soil sample is removed keeping valves A and B closed.
• Then the valve C is closed. Valve A is used to control the flow so that a constant head flow is achieved as indicated by constant level difference 'h' between the manometer tubes.
• This test can be used for highly pervious soils where falling head test cannot be used due to very rapid fall in head, which cannot be measured.
• This test cannot be used for soil with very little permeability or highly impervious soils like clay as rate of collection of water may be very low, sometimes even days, so that the rate of evaporation may be higher.
• This will give wrong results as much of the volume of collected water will evaporate.

Q4) Explain Falling Head Method as per IS 2720?

A4)

• This test is used to determine the permeability of fine-grained soils with very low permeability.
• Due to low permeability, the collected water will evaporate and will lead to wrong results in constant head test. Hence, this: test is used.
• The arrangement is shown in Fig.

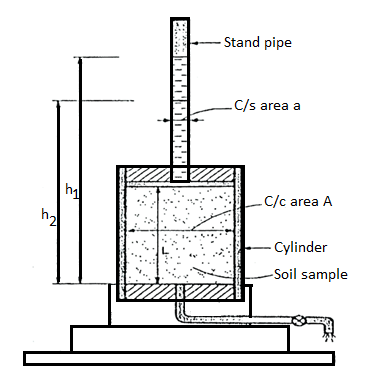
Fig.: Falling head permeability test

• A cylinder containing the soil sample is placed on a base, i.e., a perforated disc, fitted with a fine gauze. The cylinder has a rubber stopper at top in which a graduated stand pipe is fitted.
• The test is conducted by filling the standpipe with de-aired water. It is allowed to flow through the soil sample.
• During the test, the water level in the stand pipe continuously drops and the height of the water in stand pipe is measured at several time intervals and it is then recorded. Any one pair of measurements can be used to calculate the coefficient of permeability from the following formula:

K =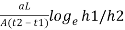

Where, a =area of c/s of stand pipe.

A =area of soil sample.

L = length of soil specimen

And h1, h2=heights of water measured in the stand pipe at time t1 and t2

If t2-t1 then

K = 2.3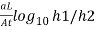

• Several pairs of readings are used in this way and average of 4-5 values gives the average coefficient of permeability.

Q5) Explain Open end test?

A5)

• In open-end test, a pipe casing is inserted into the hole of bore up to the required depth and then pipe casing is entirely cleaned out.
• Fig. Show the open-end test.

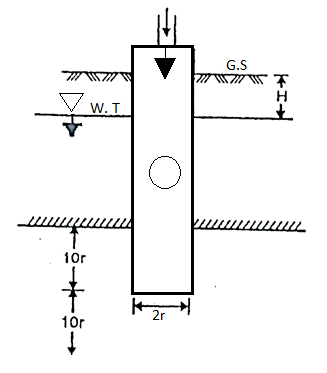
Fig.: Open end test (constant discharge)

• At the time of cleaning, the hole is kept under water if it extends below the level of water table, which prevents the possibility of squeezing of the soil into the bottom of the pipe casing at the time of removing i the driving tool.
• After cleaning the hole, hole is filled with water by a metering system. When the steady conditions are developed, that time the constant rate of flow or discharge (q) is found
• The coefficient of permeability is then found by the following expression.

K =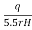

Where, K = coefficient of permeability

H = difference of level between the inlet of casing and water table

q = discharge

r= inner radius of pipe casing

• As per the requirements, the discharge 'q' can be increased by pumping-in water under pressure 'p' as shown in Fig. 2.6.6 and then the value of H becomes equal to (H+ )
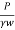• Note that for better results, the lower end of the pipe must be at a distance not less than 10r from the top and bottom of the strata.
• The open-end test can also be carried out above W.T i.e., water table as shown in Fig.
• When this test is carried out above water table, it is very difficult to make up the constant water level in pipe casing and hence some surging of this vel has to be tolerated.
• (k=can also used in this case, However, H is equal to the difference of inlet level and the bottom end of the pipe.
• As per the requirement, discharge can be increased by pumping in water under a pressure 'p' and that time total head becomes equal to (H+)

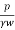Q6) Explain Darcy’s law?

A6)

• In 1856 Darcy studied and demonstrated experimentally, the velocity of laminar flow through homogeneous soil mass, which states that, "The rate of flow or the discharge per unit time is proportional to the hydraulic gradient."

q= K.i.A

V=q/A

V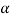i, V=Ki

Where,

q= discharge per unit time

A= total c/s area of soil mass, perpendicular to the direction of flow

i =hydraulic gradient K Darcy's coefficient of permeability

v =velocity of flow, or average discharge velocity

• If a soil sample of length 1 and cross-sectional area A, is subjected differential head of water hA-hB, the hydraulic gradient i will be equal to (hA-hB)/L and

We have,

q=KA (hA-hB)/L

When hydraulic gradient i = 1, then k=v

Q7) Explain Equivalent Hydraulic Conductivity in Stratified soil?

A7)

• Stratified soils are those, which are formed by lager upon lager of earth or dust deposited upon one another.
• If the flow is parallel to the lagers or stratification, the permeability is maximum while the flow is perpendicular direction to the stratification occurs with minimum permeability shown fig.

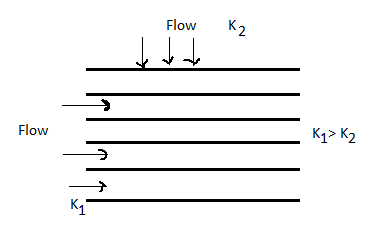
Fig.: Horizontal strata

Fig.: Vertical strata

(1) Average permeability parallel to the bedding planes

• Let L1, L2…Ln be thickness of layer.
• K1, K2…Kn be permeability of layer.
• For flow to be parallel to the bedding planes, the hydraulic gradient i will be the same for all the layers.
• However, since V Ki and K is different, the velocity of flow will different in different layers.

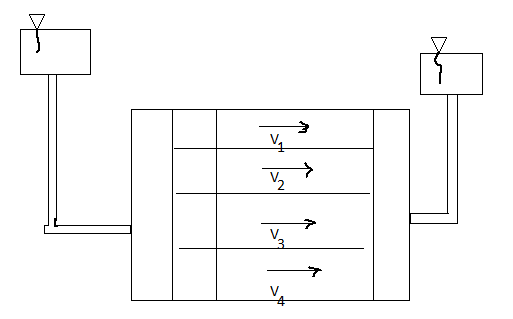
Fig.: Flow parallel to bedding plane

• Let K= average permeability of the soil deposit parallel to the bedding plane.
• Total discharge through the soil deposit sum of discharge through the individual layers.

q=q1, q2…. Qn

Kx =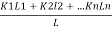

(2) Average permeability perpendicular to the bedding planes

• In this case, the velocity of flow and hence the unit discharge, will be the same through each layer. However, the hydraulic gradient and hence loss through each lager will be different. Denoting the head loss through the lagers by h1, h2….hn, and the total head loss as h we have

h=h1+h2+...hn

But h1=iL1     h2=iL2

h=iL1+iL2+iL3+…

Now, if KZ=average permeability perpendicular to the bedding plane.

We get,

Kz=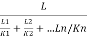

Fig.: Flow perpendicular to bedding plane

• Hence for same void ratio, the soil with rounded particles are more permeable than with angular particles.

Q8) What is Seepage?

A8)

• There is an energy transfer between the water and the soil due to the viscous friction exerted on water flowing through the soil pores.
• The pressure exerted by water on the soil through which it percolates is known as seepage pressure (Ps).

It is given by,

Ps=h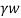

Ps = ×L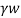

Where, h=Hydraulic head,

Z= Length over which the head (h) is lost,

i = Hydraulic gradient,

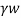=Unit weight of water

Seepage force (F) is given by,

Fs= Ps. A= i.Z.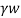A

Where A= Total cross-sectional area of the soil mass

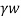=Unit weight of water

The seepage pressure always acts in the direction of the flow.

The effective pressure (P) in the soil mass is given by

Pe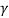=Z± iz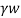

For upward flow,

Pe=Z- iz

In upward direction, the effective pressure is decreased hence-ve sign.

For downward flow,

Pe=Z+iz

In downward direction, the effective pressure is increased hence +ve sign.

Q9) What is Flow net?

A9)

• When water flows through Soil in laminar flow conditions, the paths along which the layers of water flow are called flow lines.
• Equipotential lines are the lines joining points of equal pressure along the flow lines. These can also be defined as lines along which the points have equal head of water.
• If piezometers or glass tubes are inserted along an equipotential line, water will rise to the same height in the tubes.
• Equipotential lines are always perpendicular to the flow lines.
• Analysis of seepage phenomenon is simplified by using the graphical solutions. One of the most use graphical tool is "Flow Net".
• The grid, mesh or net formed by the intersection of equipotential lines and flow lines is called flow-net.
• The portion of a flow net between two adjacent flow lines is called a low channel.
• Every section of a flow channel between two successive equipotential line is called a field.

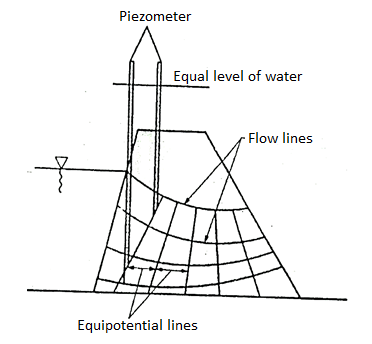
Fig.: Flow lines and equipotential line

Fig.: Flow net

Q10) What are the properties and applications of flow net?

A10)

Properties of Flow net:

• Following are the characteristic of flow-net, which are useful in construction of flow-nets and in calculation in solving seepage problems:

1. In a flow-net, flow lines and equipotential lines intersect each other at right angles.
2. The quantity of water flowing through each flow channel is the same.
3. The drop of head or potential drop between any two successive equipotential lines is the same.
4. The fields are approximately squares.
5. The flow net is representative of the flow pattern and dissipation of the hydraulic head see fig below.

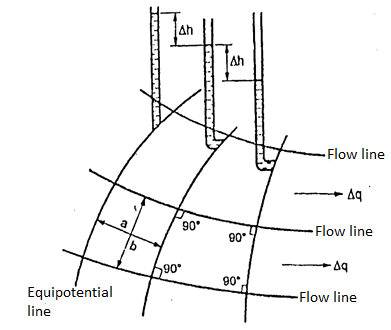
Fig.: Part of flow net illustrating characteristics

Application of Flow net:

• A flow net chart is used for following purposes:

1. Determination of discharge.
2. Determination of total head.
3. Determination of pressure head.
4. Determination of hydraulic gradient.
5. For calculating quantity of seepage.
6. For stability of earthen dam.
7. For analysis of flow phenomenon.
8. For stability analysis.

Q11) Explain Seepage calculation from a Flow net?

A11)

Fig.: Portion of flow net showing field and flow channels

The portion between two successive flow lines and successive equipotential lines is termed as field.

Let: L= Length of field and b= width of field

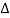h =Head drop through the field

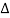q= Discharge through the flow channel

H=Difference between w/s and D/s heads

From Darcy's law of flow through soils, we know,

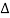q = K.i.A

Consider the unit thickness of the field,

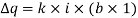
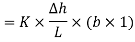
For square field, L=b, we get,

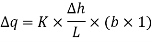
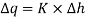∴    … (1)

Let H =Total head loss =h1-h2

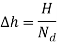
Where, Nd= Number of equipotential drops

Substituting in Equation (1), we get,

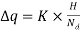∴    … (i.e., discharge through one channel)

The total discharge through the complete flow net is given as,

q =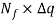

Where, Nf = Number of flow channels

=

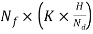
∴q =K×H×    … (2)

Equation (2) gives the seepage discharge.

is called as shape factor of the flow net.

Q12) Explain seepage through earth dam?

A12)

• Figure shows the dam section ABCD has FC as blanket filter and ENJ as top seepage line. BC represents rock line.

Steps:

1. Boundaries: EB and FC are potential boundaries and ENJ and BF are bound flow lines.
2. Sketch the first trial flow line f1f1 that emerges from EB at right angles, runs keeping the distance from top seepage line and ends at filter boundary at right angle.
3. Sketch equipotential lines P₁ P₁ P2 P2. Etc. so that they emerge and meet the boundary flow lines at right angles and form square figures.
4. Check the orthogonality and square figures in the figure Pqrs is a non-square if many figures are found to be "non-square" adjust the trial flow line and sketch new equipotential lines. There or more such trial will yield reasonably good net.

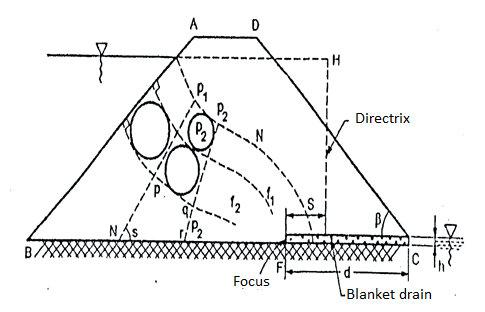
Fig.: Flow net for earthen dam

Q13) Explain Capillarity?

A13)

• The rain water which falls on the surface of earth percolates through the soil to a level is known as ground water table.
• The minutes pores of soil serve as capillary tubes through which the moisture rise above the ground water table.
• The capillary forces depend upon various factors such as

1. Surface tension of water
2. Pressure in water in relation to atmospheric pressure
3. The size and conformation of soil pores.

• In a water body consider a molecule of water, it is surrounded by other molecules. As force due to the molecular attraction act all around, the molecule is in equilibrium.
• In case of free surface, the equilibrium of molecule is disturbed as the force exerted by the water molecules below it exceeds that of the air molecules above it. In order to maintain the equilibrium, the surface assumes a curved shape. Thus, surface tension exists at the interface. Surface tension acts in the direction normal to the line drawn on the surface, and is defined as "The force per unit length at that line." As the temperature increases, surface tension decreases.

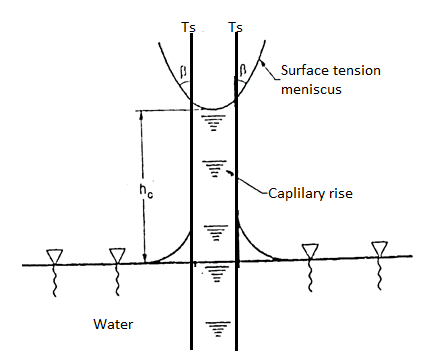
Fig.: Surface tension and meniscus formation

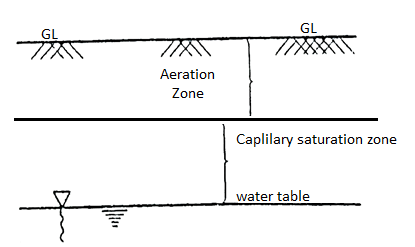
Fig.: Space above water table

• The interconnected interstices of a soil mass act as capillary tubes of varying diameter. The channels formed in a soil mass are not necessarily vertical and may be inclined in any direction.
• The space above the water table is divided into two regions.

(a)  Zone of fully saturated soil which is the capillary saturation zone.

(b) Zone of partially saturated soil which is the aeration zone.

• The height to which the capillary water noses in the soil is known as capillary fringe.
• It includes the zone of saturation and part of the zone of aeration.
• The relation between the maximum height of capillary fringe and the effective diameter is,

(he)max=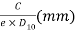

Where, C=constant which depend upon the impurity, and the shape of the particle.

e = void ratio

D10= effective diameter in mm

Q14) What is Critical Hydraulic Gradient or Quick Sand condition?

A14)

• When flow takes place in an upward direction, the effective pressure gets reduced since the seepage pressure also acts in the upward direction.
• When the seepage pressure becomes exactly equal to the submerged weight of the soil, through which the flow is taking place, the effective pressure becomes zero.
• In this case, the soil with less cohesion loses all its shear strength and soil particles move up in the direction of flow. This lifting of soil particles is known as quick sand condition or boiling sand condition during this condition the effective pressure reduces to zero.

i= ic =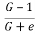

• The hydraulic gradient of the quick sand condition is known as the critical hydraulic Gradient(ic).
• Thus, quick sand condition is the particular flow condition which occurs when effective pressure reduces to zero during upward flow.

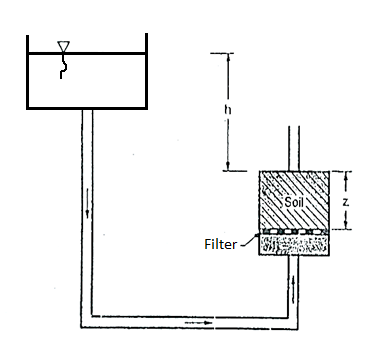
Fig.: Quick Sand Condition

Q15) What is Piping?

A15)

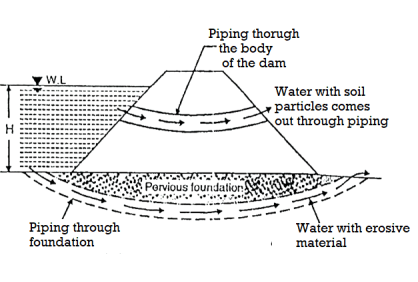
Fig.: Piping through dam and foundation

Piping through dam

• More than 25% of failures may occurs due to piping due to presence of sand and gravel there may be flow of water causing piping leakage through dam which may lead to failure of dam.
• These may develop due to faulty construction improper compaction. Shrinkage cracks, cracks developed due to settlement of the foundation such effects may be removed by better construction and maintenance.

Piping through foundation

• If soil below foundation is permeable and if foundation strata consist of cavities, then water start seeping through them which may erode the soil causing piping failure.

Sloughing of downstream toe

• It is process in which soil mass falls down after saturation. This may occur due to saturation of downstream toe. It is a type of local slope failure.
• It occurs when downstream portion of dam becomes saturated and continuously remains in same state causing piping failure.
• It may occur due to choking of downstream drains.
• Fig. Shows piping through dam and foundation to avoid the seepage failures.

Q16) The void ratio of a sand sample at the loosest and densest possible states are found to be 0.55 and 0.98 respectively. If G=2.67 determine the corresponding values of the critical hydraulic gradient?

A16)

Critical hydraulic gradient Ic=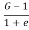

Critical gradient for loosest state,

e =0.55

∴Ic =

Critical gradient for densest state,

e =0.98

∴Ic =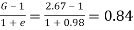

Q17) A Cylindrical mould of diameter 7.5cm contains a 15cm long sample of line sand when water flows through the soil under constant head at a rate of 58cm/min the loss of head between two points 8 cm part is found to be 12.1cm. Determine the coefficient of permeability of the soil.

A17)

A=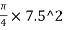

L=15cm

H=8cm

Q=q=58cm3/min

K=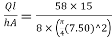

K=2.462cm/min

Q18) Determine the coefficient of permeability of soil from the following data:

Length of soil sample=25cm

Area of c/s of the sample=30cm2

Head of water=40cm

Discharge=200ml in 110sec

A18)

K =

Q19) What is the critical gradient of sand deposit of sp. Gravity=2.65 and porosity 35%.

A19)

e =0.35

∴Ic=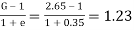

Q20) In order to compute the seepage loss through the foundation of dam, flow net was drawn. The flow net study gave number of flows channel Nf=8 and number of equipotential drop Nd=18.The head of water lost during seepage was 6m if the coefficient of permeability of foundation soil is 4×10^-5 m/min. Compute the seepage loss per meter length of dam per day.

A20)

Given:

Number of flow channels Nf=8

Number of potential drops, Nd=18

Head loss=6m

K=4×10^-5 m/min

q =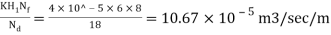

L=1m

Q=qL=10.67×10^-5×60×24

∴Q=0.154 m3/day

Q21) A sample in variable head parameter is 8cm in diameter and 10 cm high. The permeability of the sample is estimated to be 10×10^-4cm/sec. If it is desired that the head in the standpipe should fall from 24 cm to 12cm in 3 min, determine the size of the standpipe which should be used.

A21)

Given:

D=diameter of sample=8cm

K=Permeability of sample=10×10^-4cm/sec

Hl =24cm

HL =12cm

t =3minutes=180sec

L=Length of sample=10cm

a =cross sectional area of standpipe

To find the size of standpipe (i.e., d =diameter)

Let d be the diameter of standpipe to be determined

A=cross sectional area of sample=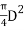

∴A=d^2

We know,

K=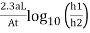

10

d =4.079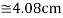

∴d=4.08cm