Unit - 5
Earth Pressure
Q1) Explain Rankine’s State of Plastic Equilibrium in soils?
A1)
- Plastic equilibrium of soil: When every point of the soil body is on the verge of failure, then a body of soil is said to be in plastic equilibrium. In another word; every point of soil mass at rest condition is brought on the verge of failure by applying tension or compression, then the state so occurred is termed as a general state of plastic equilibrium.
- Rankine's was the only engineer who developed the concepts of plastic equilibrium to solve the stability problems.
- When plastic equilibrium conditions are realized in limited zones of soil, then it is termed as the local state of plastic equilibrium. The development of earth pressure on the retaining wall is part of backfill comes under the plastic equilibrium condition.
- Rankine considered a semi-infinite mass of soil comes under a horizontal surface and a vertical boundary as shown in Fig.
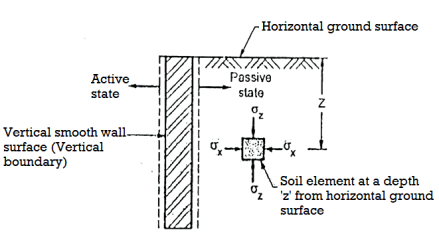
Fig.: A semi-infinite mass of soil bound by a horizontal surface and a vertical boundary
- Rankine assumed the soil mass to be homogenous, cohesionless and dry
- Consider a soil element at a depth 'e' subjected to horizontal stress and vertical stress. There are no shear stresses acting on the horizontal and vertical planes, hence
 and
and  are the principal stresses.
are the principal stresses. - When the soil mass as a whole is stressed in such way that the principal stresses of every point are in the same direction then it set up the network of failure plane. This network of failure plane is called as slip line field as shown in fig. Slip line field is equally inclined to the principal planes. When sufficient deformation of mass take place, only then plastic equilibrium is set up.
Q2) Explain Earth pressure at rest?
A2)
- It has been shown that active pressure exerted on the retaining wall resulting from slight movement of the wall away from the backfill is associated with the expansion of the soil and passive pressure exists when the movement of the retaining towards the backfill which tends to compress the soil horizontally. In short, passive pressure is associated with compression.
- When a soil element at a depth 'z' below the ground surface not subjected to any strain in the natural state, then the soil element in this condition is called as soil at rest condition. Earth pressure at rest exerted on the back of a rigid retaining wall can be determined by using the theory of elasticity in which soil is assumed to be elastic, homogeneous, isotropic and semi-infinite.
- At rest condition, the earth pressure is expressed as follows,
P0=K0  z
z
Where K0=Coefficient of earth pressure
 z=Effective vertical stress at depth a
z=Effective vertical stress at depth a
- Fig. Shows a retaining wall of height H at rest. It is possible to determine the lateral pressure by using theory of elasticity considering the soil mass to be homogenous, elastic isotropic and a semi-infinite material provided there is no displacements at all.
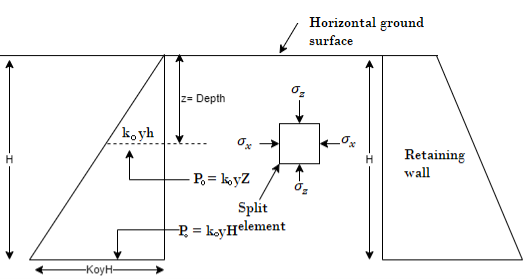
Fig.: Earth pressure at rest
Q3) Explain Earth pressure on retaining wall due to submerged backfill?
A3)
- Fig. Shows the retaining wall with backfill submerged by the natural water table saturated water. In such case, the lateral pressure is the sum of the two components.
These two components are as follows,
- Lateral pressure caused by submerged weight (
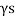 ) of the soil, k, y, z and
) of the soil, k, y, z and - Lateral pressure caused by water (
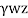 )
)
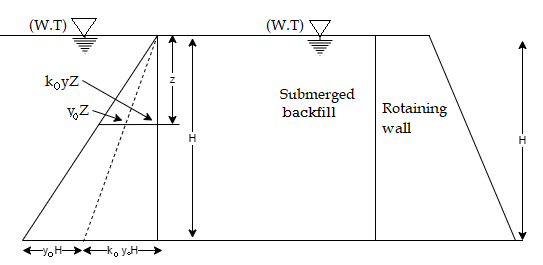
Fig.: Submerged backfill
Here at any depth 2 below the horizontal surface-active pressure is given by the following expression,
Pa=Ka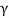 sz+
sz+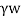 z
z
Where, Pa=active pressure
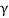 s= submerged weight of soil (y)
s= submerged weight of soil (y)
 unit weight of water
unit weight of water
Fig. Shows the active earth pressure distribution diagram at any depth 'z' and at the depth H.
The active pressure at the base of wall, where z H is given by the following expression,
Pa=Ka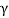 sH+
sH+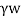 H
H
Q4) Explain Backfill with Uniform Surcharge?
A4)
- Fig. Shows the retaining wall with horizontal backfill which is loaded by a uniformly distributed surcharge of intensity "q" by assuming the vertical pressure at any, depth is increased by "q".
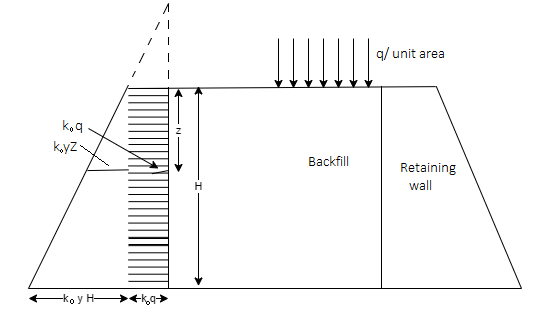
Fig.: Retaining wall with backfill carrying uniform surcharge
∴Lateral active pressure at any depth 'z' is given by the following expression
Pa=Ka z+Kaq …. (At any depth z)
z+Kaq …. (At any depth z)
Where z =H, then, active pressure at the base is given
Pa=Ka H+Kaq ......(at height H from base of wall)
H+Kaq ......(at height H from base of wall)
Q5) What is Coulomb’s Wedge theory?
A5)
- Rankine's theory of earth pressure considers the theory of plasticity approach to find the stresses in the soil mass. The Rankine's theory is only applicable to smooth vertical wall. There are various ideal conditions used in practice of retaining wall problems.
- Coulomb's wedge theory can be applied to determine the active earth pressure for a backfill possessing both cohesion and effect of friction between the backfill and wall.
- Coulomb's theory considers a dry non-cohesive or dry cohesionless inclined backfill in which the lateral earth pressure required to balance the equilibrium of a sliding wedge with a slip surface can be determined.
Basic Assumptions of Coulomb's Wedge Theory:
Following are the various basic assumptions of coulomb's wedge theory
- The backfill is dry, non-cohesive (i.e., cohesionless), homogeneous, isotropic, soil (i.e., equal elastic properties in all direction). The backfill is elastically undeformable but breakable
- Backfill possessing both cohesion and internal friction or slip surface
- The failure surface or slip surface is a plane surface which passes through the heel of wall
- Failure is two dimensional. The backfill surface is plane and can be inclined.
- The position and the line of action of the earth pressure or direction of resultant earth pressure are known. The back of the wall can be inclined to the vertical
- The sliding wedge is itself considered as rigid body and the earth pressure is obtained by considering the limiting equilibrium of the sliding wedge as a whole.
Shape of the failure surface:
- The shape of the failure surface which makes one of the boundaries of the sliding wedge is actually curved near the bottom of the wall in both active and passive cases due to wall friction. Hence there is curvature in slip surface due to friction itself.
Active earth pressure (Pa) for C= 0 backfill:
- In case of cohesionless backfill (i.e., non-cohesive backfill, C= 0), there are three forces kept the wedge under equilibrium. These three forces are:
- Weight of wedge (W)
- Soil reaction force (R) on the failure plane and
- Earth pressure reaction (P)
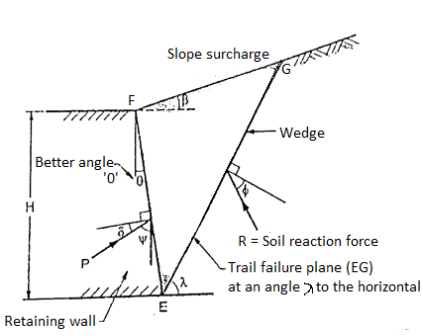
Fig.: Wedge under the action of three forces, W, R and P
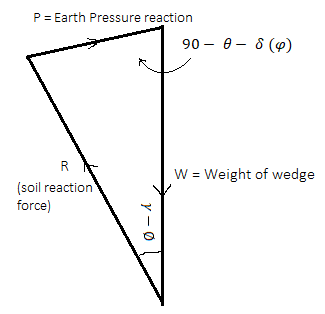
Fig.: Force triangle W, R and P
- Fig. Shows the force triangle drawn from the known value of W and direction of all the three forces and magnitude of P is determined for the assumed trial wedge.
- There is maximum wall reaction for critical step, plane and the wall should resist the maximum lateral pressure before it moves outward. Hence the maximum value of P is the active earth pressure.
- Note that in case of passive earth pressure, the wall should exert the smallest force so as to move the wedge for critical slip surface.
- In general; one of the drawbacks in coulomb's theory that it does not satisfy the static equilibrium condition. When the sliding surface is assumed to be plane, then three forces i.e., weight of wedge (W), soil reaction (R) and the earth pressure (P) acting on the sliding wedge do not meet at a common point. However, based on the other assumption, the coulomb’s theory is most effective in practice.
Active earth pressure for C- 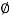 backfill:
backfill:
- Coulomb's theory can be used to find out the active earth pressure (P) for a backfill possessing both cohesion and friction.
- Following are the various forces acting on the wedge of soil at failure for C- backfill
- Weight of soil wedge (W)
- Earth pressure reaction (P) acting at an angle below the normal
- Soil reaction (R) on the failure plane acting an angle below the normal
- Force of adhesion (C2) between soil and wall
- Cohesive force (C) on the failure plane

Fig.: Forces acting on soil wedges at failure
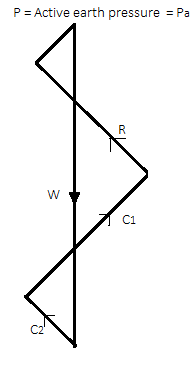
Fig.: Polygon of forces
The force polygon as shown in Fig. Is drawn from the known values of W. C, C, and direction of all five forces and the value of p i.e., active earth pressure can be determined by closing side of a polygon.
Here C1=Cu x length of the slip plane EG
C2= unit adhesion (Cw) x length of wall in contact with the soil EF
Q) Explain Rebhan’s graphical method of determination of earth pressure?
Fig.: Graphical method by poncelet construction based on Rebhan’s principles
- In 1871, Rebhan's represented a graphical method to determine the total active pressure (Pa) based on Coulomb's theory on a rough wall with a cohesionless, homogenous and inclined backfill as shown in Fig.
- Fig. Shows poncelet construction for non-cohesive soils or cohesionless soils (C = 0) based on the principles made by Rebhan.
Procedure of graphical method:
Following is the procedure of construction to find out the active earth pressure by graphical method refer Fig.
- Draw a retaining wall to a suitable scale and measure the backfill surface angle for required position as shown in Fig.
- Draw a -line EG such that it intersects the backfill surface at G.
- Draw a semi-circle BQG by taking diameter as EG.
- Draw the pressure line 'EO' at an angle of (a-5) with respect to o-line.
- Draw FI parallel to pressure line 'EO'.
- Draw a perpendicular to EG at I such that it cut the semi-circle at T.
- With centre E and radius ET, draw an are such that it cut EG at J.
- Draw JM parallel to FI
- Now EM is a rupture line
- Taking as a centre and IM as the radius draw at a such thar EG at L
After this construction from step 1 to 10, it shows the  LIM. Area of
LIM. Area of  LIM in its natural units multiplied by the unit weight of the soil (
LIM in its natural units multiplied by the unit weight of the soil ( ) gives the active earth pressure (Pa) as follows:
) gives the active earth pressure (Pa) as follows:
Pa=Area of triangle LJM= *JM*MN
*JM*MN
Where,  =unit wt of the soil
=unit wt of the soil
JM length of a triangle LJM
MN=height of  LJM
LJM
Pa=Active earth pressure
Q6) What is Finite & Infinite slopes?
A6)
Infinite slope:
- The boundary surface of a semi-infinite soil mass having the constant soil properties for all identical depths below the surface is called as infinite slope.
- The Fig. Shows an infinite slope with its traverse extent large as compared to the depth of its failure zone.
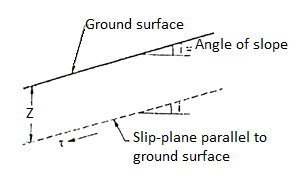
Fig.: An infinite slope
- Slopes extending to infinity do not exist in nature.
Finite slopes:
- When the slope is having the limited extent, then it is called as finite slopes. Most man-made embankments and road or railway, cuts etc. are finite in extent.
- Examples of finite slopes: Inclined faces of earth dam, embankments, cuts etc. are the examples of finite slopes.
- Fig. Shows the finite slopes.
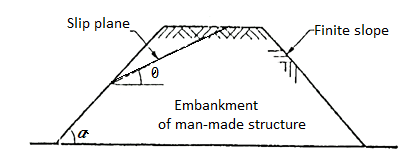
Fig.: Embankment
Fig.: Cut slope
Q7) What are the types of Slope failure?
A7)
- There are various failure types of infinite and finite slopes. The failure of the slopes can be in the form of plane slide (i.e., translational slide) or rotational slick failure along essentially planer surface is called translational slides:
Modes of failure in Infinite slopes
- For an infinite slope in a homogeneous soil, failure of slope take place due to sliding of the soil mass along a plane parallel to the ground surface at a certain depth. In short, for long steep slope, failure of slope will be along a surface parallel to the ground surface and in such case sliding surface is plane as shown in Fig.
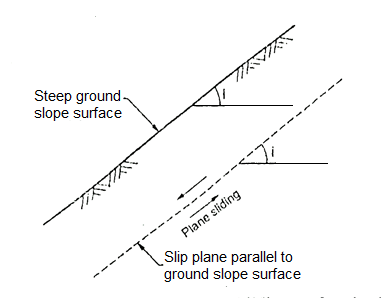
Fig.: Failure in infinite slope
Modes of failure in Finite slopes:
- There are three basic modes of failure in case of finite slopes.
- Face failure or slope surface
- Toe failure
- Base failure
1. Face failure or slope surface
- When the failure occurs along a surface of sliding interests the slope above the toe, then slide is termed as slope failure or face failure.
- This type of failure occurs due to very high slope angle (i) and soil close to the toe is quite strong or the soil the upper part of the slope is comparatively weak.
- Fig. Shows plane slide and rotational slide respectively in case of slope failure, face failure.
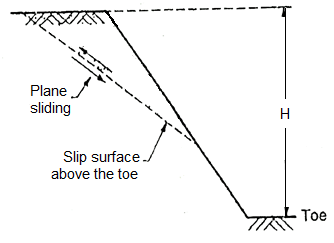
Fig.: Plane side of Face failure
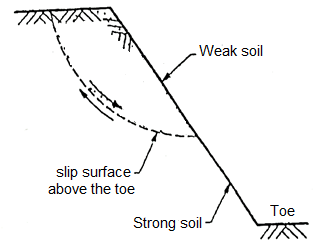
Fig.: Rotational side of face failure
2. Toe failure
- When the failure surface passes through the toe of slope, then it is termed as toe failure. Toe failure is most common mode of failure and occurs in steep slope consisting of the homogeneous solid mass above and below the base.
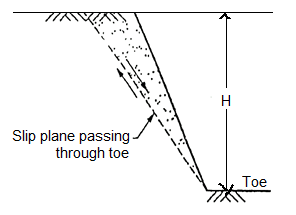
Fig.: Plane side of Toe failure
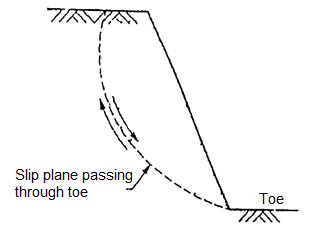
Fig.: Rotational side of toe failure
3. Base failure
- When the failure surface passes below the toe of slope, then it is termed as base failure. This type of failure occurs due to the weaker material or relatively weak and soft soil at the base than that of slope. Fig. Shows the base failure.
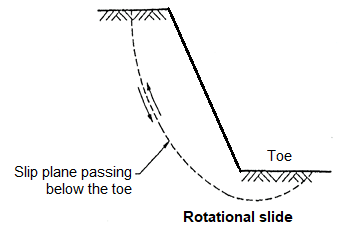
Fig.: Modes of base failure
Q8) Explain Culmann’s method & Method of Slices?
A8)
- Culmann's graphical method is rather general method than Rebhan's method. This method is same as the trial wedge method. The force triangle or force polygon can directly be constructed on o-line EG considering EG as a load line.
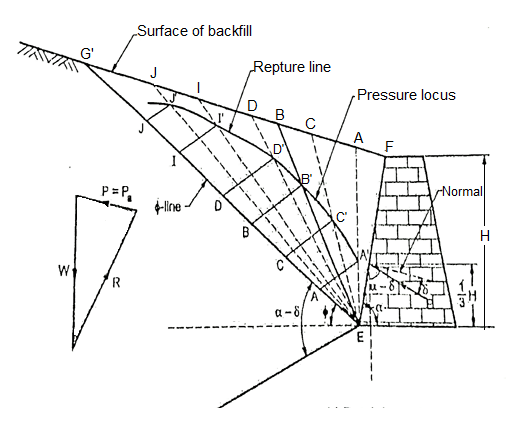
Fig.: Culmann’s graphical method for determining active earth pressure
- This method can be used to evaluate the coulomb's earth pressure fr ground sa face of any configuration, different types of surcharges and layered backfills.
- Fig. Shows the Culmann's graphical method of determine active earth pressure (P) for non-cohesive soils or cohesionless soils (i.e., C= 0)
Graphical construction procedure:
- Various steps involved in the procedure are as follows:
- EF it a retaining wall as shown in Fig. 5 in 1(a) drawn to a suitable scale.
- Draw -line EG at an angle with respect to horizontal.
- Mark on EG, the distances EA, EC, ED, EL, EJ etc. to a suitable scale representing the weight of wedges EFA, EFC, EFD, EFI, EFI etc. respectively.
- Draw lines parallel to pressure line ET from the points A, C, D, I J such that it intersects assumed rupture line EA, EC, ED, EI, EJ at points A, C, D,1, J respectively.
- Then point A', C, D, I', J' are joined by a smooth curve representing the pressure locus.
- Select point B' on the pressure locus in such way that the tangent to the curve at this point parallel to line EG
- Draw B'B parallel to the pressure line ET. The magnitude of B'B" itself in its natural units gives the active earth pressure (Pa)
- Points E and B' are joined and extended further so as to meet the surface of backfill at B Then EB is the rupture line.
- Note that, for the plane backfill surface, the point of application of active earth pressure (Pa) is at a height 1/3 of from the base of retaining wall.
Q9) What is Stability Number & chart?
A9)
- The slipping along the slip is at critical equilibrium is resisted by the total cohesive force (CL). This force is proportional to the cohesion C and the height H of the slope.
- The force responsible for instability of i se slope is the weight of the wedge which is equal to the unit weight
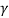 .
.
∴Weight of the wedge 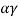 H2
H2
- Let (F.S) c be the factored of safety for cohesion.
We know,
=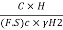
=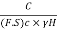 =Sn …. (1)
=Sn …. (1)
- Here
 is the dimensionless quantity which is called as Tayler's stability number (Sn).
is the dimensionless quantity which is called as Tayler's stability number (Sn). - Consider Cm be mobilized unit cohesion which is essential so as to have the equilibrium of a slope having height H.
Cm= … (2)
… (2)
Where C= Cohesion:
(F.S) c= Factor of safety with respect to cohesion
Hence the Equation (1) can be written as follows:
Sn =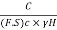 =
=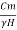 …. (3)
…. (3)
- Also, for critical height H the factor of safety with respect to height (H) is equal to the factor of safety with respect to cohesion (C)
∴ (F.C) c =Hc/H… (4)
Where (F.C) c = Factor of safety with respect to cohesion
There Equation (3) becomes as
Sn =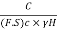 =
=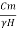 … (5)
… (5)
- Taylor analyzed the friction circle method and determined the values of stability number (Sn) for finite slopes and prepared the table as shown in Table gives the values of Sn for the various values of and slope angle (i).
- When a dangerous circle passing below the toe occurs, then stability numbers such as (0.145). (0.068) and (0.023) mentioned in Table indicates the most dangerous circle through toe.
- The Fig. Shows Taylor's stability number charts for
 =0
=0

Fig.: Taylor’s stability number charts, =0 with respect to depth factor
=0 with respect to depth factor
Q10) Compute the active earth pressure at a depth of 4.5 m in a sand whose angle of friction is 37 degree and Density of 15.60 KN/m3 in dry state.
A10)
Given:
H = 4.5 m, 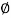 = 37⁰,
= 37⁰,
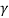 = 15.60 kN/m²
= 15.60 kN/m²
To compute the active earth pressure at a depth H in dry state
We know, From Rankine's theory, active earth pressure (Pa) at a depth H is given by:
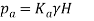 … (1)
… (1)
Where Ka=coefficient of active earth pressure=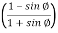
∴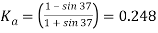
Substituting
Ka = 0.248 in Equation (1), we get
Pa = 0.248 x 15.60x4.5
∴Pa = 17.4 kN/m3
Q11) A retaining wall with a vertical smooth back is 8m high It supports a cohesionless soil with  30% The surface of soil is horizontal. Determine the thrust in the wall.
30% The surface of soil is horizontal. Determine the thrust in the wall.
A11)
Given:
H=8m,  = 19 kN/m²,
= 19 kN/m², 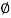 =30°.
=30°.
To determine the thrust (Pa) in wall: From the given data, draw the Fig. For better understanding.

Fig.: Active earth pressure distribution diagram and retaining wall resp.
For the condition given here, Rankine's theory disregards the friction between the soil and back of the wall. Total thrust (Pa) per meter of wall by Rankine's theory of earth pressure is given by:
Pa=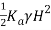 … (1)
… (1)
Where ka = coefficient of active earth pressure=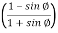
Ka=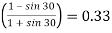
Substituting the ka = 0.33, H=8 m and 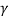 = 19 kN/m3 in Equation (1), we get
= 19 kN/m3 in Equation (1), we get
Pa=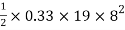
∴Pa=200.64 KN per meter of wall
Active earth pressure (Pa) at the base of wall is given by:
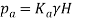 …. (Active earth pressure at the base of wall)
…. (Active earth pressure at the base of wall)
Pa = 0.33 x 19 x8 = 50.16 kN/m2
∴Pa=50.16KN/m2
Q12) A smooth vertical wall retains a level backfill with 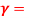 18 kN/m3 and c=0 to a depth of 8 m: Draw the lateral earth pressure diagram, and compute the total active earth pressure with its point of application
18 kN/m3 and c=0 to a depth of 8 m: Draw the lateral earth pressure diagram, and compute the total active earth pressure with its point of application
A12)
Given: 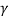 = 18 kN/m²,
= 18 kN/m²,  = 33
= 33 .
.
C=0 (i.e., cohesionless soil), H=8 m
To compute total active earth pressure (Pa) with its point of application
For the condition given here, Rankine's theory disregards the friction between the soil and back of the wall. Note that given wall is a smooth vertical wall. Hence use Rankine's theory of earth pressure.
There is no surcharge being a level backfill.
Total active earth pressure (Pa) is given by the Rankine's theory of earth pressure as,
Pa = …. (1)
…. (1)
Where ka= coefficient of active earth pressure=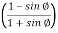
Ka=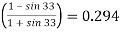
Substituting Ka= 0.294,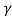 = 18 kN/m² and H=8m in equation (1)
= 18 kN/m² and H=8m in equation (1)
We get, Pa =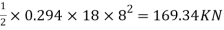
Hence total active earth pressure (Pa) is 169.34 kN per metre length of wall.
Point of application of Pa is 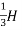 from the base of wall.
from the base of wall.
∴Point of application of Pa= x8=2.666
x8=2.666 2.67 m = 2.67m from base of wall
2.67 m = 2.67m from base of wall
Draw Lateral earth pressure diagram
Pa= active earth pressure at the base of wall = 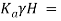 0.294 x 18x8=42.33 kN/m²
0.294 x 18x8=42.33 kN/m²
From the obtained values of active earth pressure, lateral earth pressure diagram is drawn as shown in Fig.
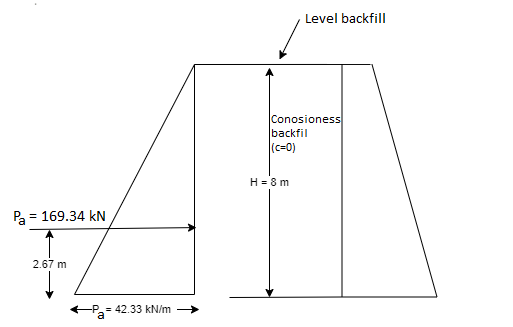
Fig.: Lateral earth pressure and smooth vertical wall resp.
Q13) A smooth vertical wall retains a level surface with  =18 kN/m3
=18 kN/m3 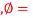 30
30 to a depth of 8 m. Draw the lateral pressure diagram and compute the total active pressure in dry condition and when water table rises to the GL Assume=22 kN/m3.
to a depth of 8 m. Draw the lateral pressure diagram and compute the total active pressure in dry condition and when water table rises to the GL Assume=22 kN/m3.
A13)
Given: H=depth=8m; 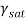 =22 kN/m3,
=22 kN/m3, 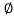 = 30°;
= 30°; 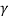 = 18 kN/m3
= 18 kN/m3
To compute the total active pressure (Pa) in dry condition:
Ka= Coefficient of active earth pressure= 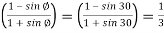
∴Total active earth pressure in dry condition (Pa)= 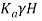 =
=  × 18 × 8
× 18 × 8
∴Pa= 48 kN/m²
To compute the total active earth pressure when water table rises to the GL (i.e., submerged soil
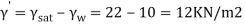
:. Total active earth pressure (Pa) = 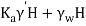 =
=  x12x8+10x8
x12x8+10x8
∴Pa = 112 kN/m²
Q14) A cohesionless soil deposit having unit weight of 15 KN/m3 and angle of internal friction  . Determine the active and passive lateral pressure intensities at depth of 10 m.
. Determine the active and passive lateral pressure intensities at depth of 10 m.
A14)
Given:
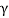 = unit weight = 15 kN/m3,
= unit weight = 15 kN/m3,
H = 10m
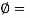 Angle of internal friction = 30
Angle of internal friction = 30 ,
,
To determine coefficient of active earth pressure (Ka) and coefficient of passive earth pressure (Kp)
Ka= Coefficient of active earth pressure= 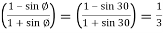
Kp= Coefficient of passive earth pressure= 
To determine active and passive lateral pressure intensities at a depth of 10 m
1) Active lateral pressure (Pa)
Pa=  =
=  × 15 × 10
× 15 × 10
∴Pa=50KN/m2
2) Passive lateral pressure (Pp)
Pp= 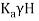 = 3× 15 × 10
= 3× 15 × 10
∴Pp=450KN/m2