Engineering Mathematics-II
Unit VSolid GeometryFind the Cartesian co-ordinates of a pointe whose spherical polar co-ordinates are (2, , ) Find the spherical polar co-ordinates of a the points whose Cartesian co-ordinates are (i) (3, 4, 5) (ii) (– 1, 1, – 1) 3. Find the cylindrical co-ordinates of the point whose Cartesian co-ordinates are (– 3, 4, 12)4. Find (i)Spherical polar (ii) cylindrical equation of surfaces whose Cartesian equations are (a)x2 + y2 = a2 (b) x2 + y2 + z2 = 16.5. Find the equation of sphere passing through the points (1 ,3 ,1 ), (2 ,- 1 ,1 ), (1 ,2 ,0 ), (1 ,- 1 ,1 ).6. Find the equation of sphere which passes through origin and makes equal intercepts of unit length on the axes. 7. Prove that the spheres x2 + y2 + z2 – 2x + 4y – 4z = 0 and x2 + y2 + z2 + 10 x + 2z + 10 = 0 touch each other. Find the co-ordinates of point of contact.8. Find the equation of sphere which has its centre at (2, 3, –1) and touches the line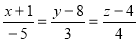 
9. Find the equation of sphere touching three co-ordinate planes and the plane 2x + y + 2z = 6. 10. Find the equation of sphere which passes through the point (2, – 2, 1) and touches the plane 2x – y – 2z = 4 at (1, 2, – 2)11. Prove that the sphere x2 + y2 + z2 + 2x – 4y – 2z – 3 = 0 touch the plane 2x – 2y + z + 14 = 0 and find the co-ordinates of point of contact. 12. Find the equation of sphere tangential to the plane x – 2y – 2z = 7 at (3, – 1, – 1) and passing through the point (1, 1, – 3).13. A sphere S has points (1, –2, 3) and (4, 0, 6) as opposite ends of diameter. Find the equation of the sphere having the intersection of S with the plane x + y – 2z + b = 0 as its great circle.14. Find the equation of cone whose vertex is at origin and guiding curve is given by + = 1 and z = c15. Find the equation of cone whose vertex is at origin and guiding curve is given by x2 – 2y2 + 3z2 = 4x + 9, x + y – z = 4.16. Find the equation of Right circular cone whose vertex is at the origin, whose axis is the line = = and which has semi vertical angle of 30.17. Find the equation of right circular cone whose vertex is (1, – 1, 2) and axis is the line = = and semi vertical angle 45 18. Find the equation of a right circular cone whose vertex at (1, – 1,1), semi-vertical angle 45 and its axis is perpendicular to the plane 2x + y – 2z + 1 = 0.19. Find the equation of a right circular cone whose vertex at (1, – 1,1), semi-vertical angle 45 and its axis is perpendicular to the plane 2x + y – 2z + 1 = 020. Find the equation of right circular cylinder with radius 2 units, whose axis passes through the point (1,2,3) and has direction consines proportional to 2, – 3, 6.
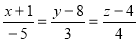9. Find the equation of sphere touching three co-ordinate planes and the plane 2x + y + 2z = 6. 10. Find the equation of sphere which passes through the point (2, – 2, 1) and touches the plane 2x – y – 2z = 4 at (1, 2, – 2)11. Prove that the sphere x2 + y2 + z2 + 2x – 4y – 2z – 3 = 0 touch the plane 2x – 2y + z + 14 = 0 and find the co-ordinates of point of contact. 12. Find the equation of sphere tangential to the plane x – 2y – 2z = 7 at (3, – 1, – 1) and passing through the point (1, 1, – 3).13. A sphere S has points (1, –2, 3) and (4, 0, 6) as opposite ends of diameter. Find the equation of the sphere having the intersection of S with the plane x + y – 2z + b = 0 as its great circle.14. Find the equation of cone whose vertex is at origin and guiding curve is given by + = 1 and z = c15. Find the equation of cone whose vertex is at origin and guiding curve is given by x2 – 2y2 + 3z2 = 4x + 9, x + y – z = 4.16. Find the equation of Right circular cone whose vertex is at the origin, whose axis is the line = = and which has semi vertical angle of 30.17. Find the equation of right circular cone whose vertex is (1, – 1, 2) and axis is the line = = and semi vertical angle 45 18. Find the equation of a right circular cone whose vertex at (1, – 1,1), semi-vertical angle 45 and its axis is perpendicular to the plane 2x + y – 2z + 1 = 0.19. Find the equation of a right circular cone whose vertex at (1, – 1,1), semi-vertical angle 45 and its axis is perpendicular to the plane 2x + y – 2z + 1 = 020. Find the equation of right circular cylinder with radius 2 units, whose axis passes through the point (1,2,3) and has direction consines proportional to 2, – 3, 6.
0 matching results found