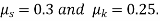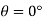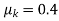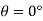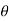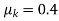Que. No. | Question Description | ||
| D’Alembert’s Principle - Rectilinear Motion | ||
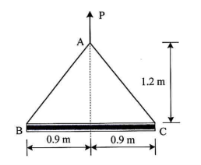
1 |
| ||
2 | A motorist travelling at a speed of 108 kmph suddenly applied the brakes and comes to a stop after skidding 75m. Determine- A) the time required for car to stop B) The co-efficient of friction between Tyres and pavement. | ||
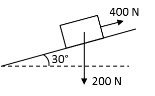
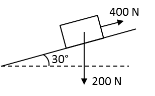
3 | A block of weight 200 N is resting on the inclined plane as shown in figure. If 400 N force is applied to the block, then determine the total acceleration of the block if
| ||
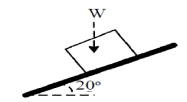
4 | A 50 kg body is initially at rest on a 20° inclined plane with coefficient of kinetic friction µ= 0.25. Find the distance and the time body travels before attaining the speed of 15m/s. |
| |
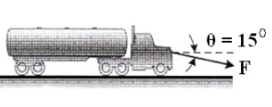
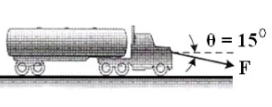
5 | The 4.5 x106 kg tanker is pulled with constant acceleration of 0.001 m/s2 using cable that makes an angle of 15° with the horizontal as shown in Fig. Determine the force in the cable using Newton’s second law of motion. |
| |
6 | The tanker is pulled with constant acceleration of 0.001 m/s2 using cable that makes an angle of 100 with the horizontal as shown in Fig. If the force in the cable is 45.694 kN, determine the mass of tanker using Newton’s 2nd law of motion. |
| |
7 | During a break test, the car of mass 1500 kg is stop from an initial speed of 100 kmph in a distance of 50 m. Determine the breaking force assuming uniform deceleration. | ||
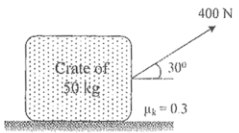
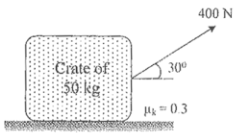
8 | A 50 kg crate shown in Fig. rests on a horizontal plane for which the coefficient of kinetic friction is µk = 0.3. If the crate does not tip over when it is subjected to a 400 N towing force as shown, determine the velocity of the crate in 5 s starting from rest.
| ||
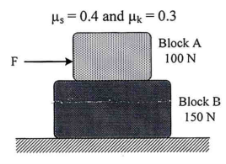
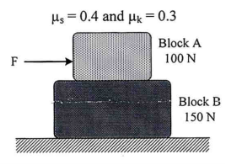
9 | Block B rests on smooth surface. If the coefficient of static and kinetic friction between A and B are µs = 0.4 and µk = 0.3 respectively, determine the acceleration of each block if block A is pushed with a force F (a) 30 N (b) 250 N. Refer Fig.
| ||
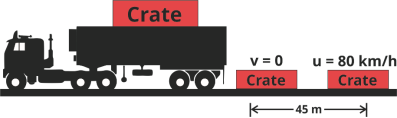
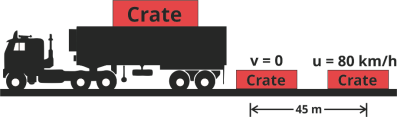
10 | A crate having mass of 60 kg falls horizontally of the back of truck which is traveling at 80 km/h. Determine the coefficient of kinetic friction between the road and the crate, If the crate slides 45 m on the ground with no tumbling along the road before coming to rest. Assume the initial velocity of the crate along the road be 80 km/h. Refer given figure.
| ||
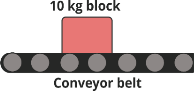
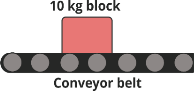
11 | The conveyor belt is designed to transport packages of various weights shown in Fig. Each 10 kg package has a coefficient of kinetic friction μk = 0.15. If the speed of the conveyor is 5m/s, and then it suddenly stop, determine the distance the package will slide on the belt before coming to rest.
| ||
| D’Alembert’s Principle – Curvilinear Motion | ||
1 | The pendulum bob has a mass m kg and is released from rest when θ = 0°. Determine the tension in the cord as a function of the angle of decent θ. Neglect the size of bob. OR
A bob of pendulum having mass ‘m’ and attached to a cord of Length L is released from initial position
| ||
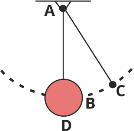
2 | A pendulum bob has a mass of 10 kg and is released from rest when θ = 0 as shown in Fig. Determine the tension in the cord at θ = 300. Neglect the size of bob.
| ||
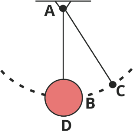
3 | A 60 kg wreeking ball B is attached to a 15 m long steel cable AB and swing in vertical arc shown. Determine the tension in the cable (a) at the top C of the swing, (b) at the bottom D of the swing, where the speed of B is 4.2 m/s.
| ||
4 | A car is moving on a hump with radius 50 m along the road at a speed of 40 kmph. Knowing
| ||
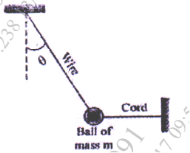
5 | The small ball of mass m and its supporting wire becomes a simple pendulum when the horizontal cord is served. Determine the ratio of the tension T in the supporting wire immediately after the cord is cut to that in the wire before the wire is cut. |
| |
| Work Energy Principle, Impulse Momentum Theorem | ||
1 |
| ||
2 | A ball has a mass of 30 kg and is thrown upward with a speed of 15 m/s. Determine the time to attain maximum height using impulse momentum principle. Also find the maximum height. | ||
3 | A block of 7.25 kg slides 150 mm from rest down the 20° inclined plane as shown in Fig. It hits a spring whose modulus is 1750 N/m. If µk = 0.20, determine the maximum compression of the spring. Use Work Energy principle.
| ||
4 | A woman having a mass of 70 kg stands in an elevator which has a downward acceleration of 4 m/s2 starting from rest. Determine work done by her weight and the work of the normal force which the floor exerts on her when the elevator descends 6 m. | ||
5 | A ball has a mass of 30 kg is thrown upward with a speed of 15 m/s. Determine the time and distance travelled by the ball before stopping. Use impulse momentum principle. | ||
6 | A 2 kg stone is dropped from a height h and strike the ground with a velocity of 24 m/s. find the kinetic energy of the stone as it strikes the ground and the height h from which it was dropped. Use work energy method. | ||
7 | A railroad car having a mass of 15 Mg is coasting at 1.5 m/s on a horizontal track. At the same time another car having a mass of 12 Mg is coasting at 0.75 m/s in the opposite direction. If the car meet and couple together, determine the speed of both cars just after the coupling. | ||
8 | A block weighing 200 N is pulled up a 300 plane by a force P producing a velocity of 5 m/s in 5 s. If the coefficient of friction is 0.2, determine the magnitude of force P using impulse momentum principle. | ||
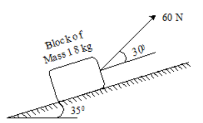
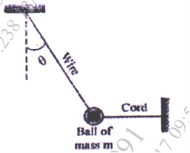
9 | Determine the work done by all forces acting on the block of 18 kg as shown in Fig. as it moves 12 m upwards along the plane. Take coefficient of kinetic friction as 0.2. |
| |
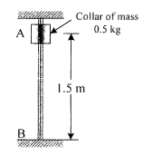
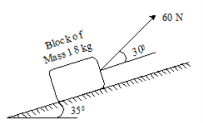
10 | The small collar of mass 0.5 kg is released from rest at A and strikes the base B with velocity 4.7 m/s as shown in Fig. , determine the work done by frictional force using work energy principle. |
| |
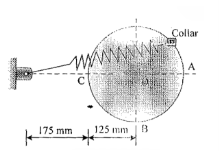
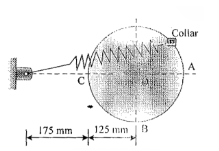
11 | A 1.5 kg collar is attached to a spring and slides without friction along a circular rod in a horizontal plane. The spring has an undeformed length of 150 mm and a constant k = 400 N/m. Knowing that the collar is in equilibrium at A and is given a slight push to get moving, determine the velocity of the collar as it passes point B. Refer fig. |
| |
12 | Each of the cable can sustain maximum tension of 25 kN. If the uniform beam has a weight of 25 kN, determine the shortest time possible to lift, the beam with a speed of 3 m/s starting from rest by impulse momentum principle. Refer Fig. |
| |
| IMPACT | ||
1 | Explain the types of impacts based on the properties of the bodies. | ||
2 | A small rubber ball is released from a height of 800 mm on horizontal floor. After the first bounce it rises to a height of 480 mm. Compute the coefficient of restitution. Upto what height it will rise after the second bounce? | ||
3 | Ball A of mass 0.35 kg moving with an initial velocity 3 m/s collides with ball B of mass 0.2 kg which is at rest. If perfect elastic collision occurs between the two balls, Determine the velocities of both the balls after collision. | ||
4 | A tennis ball is dropped from a height of 1600 mm and it rebounds to a height of 1100mm. Determine the coefficient of restitution. | ||
5 | One of the requirement for tennis balls to be used in official competition is that, when dropped onto a rigid surface from a height of 2540 mm, the height of the first bounce of the ball must be in the range of 1346 mm ≤ h ≤ 1473 mm. Determine the range of the coefficient of restitution of the tennis balls satisfying this requirement. | ||
6 | A ball is dropped from an unknown height on a horizontal floor from which it rebounds to height of 8 m. If e = 0.667, calculate the height from which the ball was dropped. | ||
7 | A bullet moving at a speed of 300 m/s has its speed reduce to 270 m/s when it passes through a board. Determine how many such hoards the bullet will penetrate before it stops. | ||
8 | A 15 kg wagon moving with a speed of 0.5 m/s towards right collides with 35 kg wagon which is at rest. If 35 kg wagon is observed to move towards right after collision at a speed of 0.3 m/s, determine the coefficient of restitution between two. Also Comment on the impact. | ||
9 | Two masses of 15 kg and 20 kg are moving along straight line towards each other at a velocities of 4 m/s and 2 m/s respectively. If restitution observed was 60 % , find the velocities of both masses immediately after impact. Also find the loss in Kinetic Energy & percentage loss in Kinetic Energy. | ||
Que. No. | Question Description | ||
| D’Alembert’s Principle - Rectilinear Motion | ||
1 |
| ||
2 | A motorist travelling at a speed of 108 kmph suddenly applied the brakes and comes to a stop after skidding 75m. Determine- A) the time required for car to stop B) The co-efficient of friction between Tyres and pavement. | ||
3 | A block of weight 200 N is resting on the inclined plane as shown in figure. If 400 N force is applied to the block, then determine the total acceleration of the block if
| ||
4 | A 50 kg body is initially at rest on a 20° inclined plane with coefficient of kinetic friction µ= 0.25. Find the distance and the time body travels before attaining the speed of 15m/s. |
| |
5 | The 4.5 x106 kg tanker is pulled with constant acceleration of 0.001 m/s2 using cable that makes an angle of 15° with the horizontal as shown in Fig. Determine the force in the cable using Newton’s second law of motion. |
| |
6 | The tanker is pulled with constant acceleration of 0.001 m/s2 using cable that makes an angle of 100 with the horizontal as shown in Fig. If the force in the cable is 45.694 kN, determine the mass of tanker using Newton’s 2nd law of motion. |
| |
7 | During a break test, the car of mass 1500 kg is stop from an initial speed of 100 kmph in a distance of 50 m. Determine the breaking force assuming uniform deceleration. | ||
8 | A 50 kg crate shown in Fig. rests on a horizontal plane for which the coefficient of kinetic friction is µk = 0.3. If the crate does not tip over when it is subjected to a 400 N towing force as shown, determine the velocity of the crate in 5 s starting from rest.
| ||
9 | Block B rests on smooth surface. If the coefficient of static and kinetic friction between A and B are µs = 0.4 and µk = 0.3 respectively, determine the acceleration of each block if block A is pushed with a force F (a) 30 N (b) 250 N. Refer Fig.
| ||
10 | A crate having mass of 60 kg falls horizontally of the back of truck which is traveling at 80 km/h. Determine the coefficient of kinetic friction between the road and the crate, If the crate slides 45 m on the ground with no tumbling along the road before coming to rest. Assume the initial velocity of the crate along the road be 80 km/h. Refer given figure.
| ||
11 | The conveyor belt is designed to transport packages of various weights shown in Fig. Each 10 kg package has a coefficient of kinetic friction μk = 0.15. If the speed of the conveyor is 5m/s, and then it suddenly stop, determine the distance the package will slide on the belt before coming to rest.
| ||
| D’Alembert’s Principle – Curvilinear Motion | ||
1 | The pendulum bob has a mass m kg and is released from rest when θ = 0°. Determine the tension in the cord as a function of the angle of decent θ. Neglect the size of bob. OR
A bob of pendulum having mass ‘m’ and attached to a cord of Length L is released from initial position
| ||
2 | A pendulum bob has a mass of 10 kg and is released from rest when θ = 0 as shown in Fig. Determine the tension in the cord at θ = 300. Neglect the size of bob.
| ||
3 | A 60 kg wreeking ball B is attached to a 15 m long steel cable AB and swing in vertical arc shown. Determine the tension in the cable (a) at the top C of the swing, (b) at the bottom D of the swing, where the speed of B is 4.2 m/s.
| ||
4 | A car is moving on a hump with radius 50 m along the road at a speed of 40 kmph. Knowing
| ||
5 | The small ball of mass m and its supporting wire becomes a simple pendulum when the horizontal cord is served. Determine the ratio of the tension T in the supporting wire immediately after the cord is cut to that in the wire before the wire is cut. |
| |
| Work Energy Principle, Impulse Momentum Theorem | ||
1 |
| ||
2 | A ball has a mass of 30 kg and is thrown upward with a speed of 15 m/s. Determine the time to attain maximum height using impulse momentum principle. Also find the maximum height. | ||
3 | A block of 7.25 kg slides 150 mm from rest down the 20° inclined plane as shown in Fig. It hits a spring whose modulus is 1750 N/m. If µk = 0.20, determine the maximum compression of the spring. Use Work Energy principle.
| ||
4 | A woman having a mass of 70 kg stands in an elevator which has a downward acceleration of 4 m/s2 starting from rest. Determine work done by her weight and the work of the normal force which the floor exerts on her when the elevator descends 6 m. | ||
5 | A ball has a mass of 30 kg is thrown upward with a speed of 15 m/s. Determine the time and distance travelled by the ball before stopping. Use impulse momentum principle. | ||
6 | A 2 kg stone is dropped from a height h and strike the ground with a velocity of 24 m/s. find the kinetic energy of the stone as it strikes the ground and the height h from which it was dropped. Use work energy method. | ||
7 | A railroad car having a mass of 15 Mg is coasting at 1.5 m/s on a horizontal track. At the same time another car having a mass of 12 Mg is coasting at 0.75 m/s in the opposite direction. If the car meet and couple together, determine the speed of both cars just after the coupling. | ||
8 | A block weighing 200 N is pulled up a 300 plane by a force P producing a velocity of 5 m/s in 5 s. If the coefficient of friction is 0.2, determine the magnitude of force P using impulse momentum principle. | ||
9 | Determine the work done by all forces acting on the block of 18 kg as shown in Fig. as it moves 12 m upwards along the plane. Take coefficient of kinetic friction as 0.2. |
| |
10 | The small collar of mass 0.5 kg is released from rest at A and strikes the base B with velocity 4.7 m/s as shown in Fig. , determine the work done by frictional force using work energy principle. |
| |
11 | A 1.5 kg collar is attached to a spring and slides without friction along a circular rod in a horizontal plane. The spring has an undeformed length of 150 mm and a constant k = 400 N/m. Knowing that the collar is in equilibrium at A and is given a slight push to get moving, determine the velocity of the collar as it passes point B. Refer fig. |
| |
12 | Each of the cable can sustain maximum tension of 25 kN. If the uniform beam has a weight of 25 kN, determine the shortest time possible to lift, the beam with a speed of 3 m/s starting from rest by impulse momentum principle. Refer Fig. |
| |
| IMPACT | ||
1 | Explain the types of impacts based on the properties of the bodies. | ||
2 | A small rubber ball is released from a height of 800 mm on horizontal floor. After the first bounce it rises to a height of 480 mm. Compute the coefficient of restitution. Upto what height it will rise after the second bounce? | ||
3 | Ball A of mass 0.35 kg moving with an initial velocity 3 m/s collides with ball B of mass 0.2 kg which is at rest. If perfect elastic collision occurs between the two balls, Determine the velocities of both the balls after collision. | ||
4 | A tennis ball is dropped from a height of 1600 mm and it rebounds to a height of 1100mm. Determine the coefficient of restitution. | ||
5 | One of the requirement for tennis balls to be used in official competition is that, when dropped onto a rigid surface from a height of 2540 mm, the height of the first bounce of the ball must be in the range of 1346 mm ≤ h ≤ 1473 mm. Determine the range of the coefficient of restitution of the tennis balls satisfying this requirement. | ||
6 | A ball is dropped from an unknown height on a horizontal floor from which it rebounds to height of 8 m. If e = 0.667, calculate the height from which the ball was dropped. | ||
7 | A bullet moving at a speed of 300 m/s has its speed reduce to 270 m/s when it passes through a board. Determine how many such hoards the bullet will penetrate before it stops. | ||
8 | A 15 kg wagon moving with a speed of 0.5 m/s towards right collides with 35 kg wagon which is at rest. If 35 kg wagon is observed to move towards right after collision at a speed of 0.3 m/s, determine the coefficient of restitution between two. Also Comment on the impact. | ||
9 | Two masses of 15 kg and 20 kg are moving along straight line towards each other at a velocities of 4 m/s and 2 m/s respectively. If restitution observed was 60 % , find the velocities of both masses immediately after impact. Also find the loss in Kinetic Energy & percentage loss in Kinetic Energy. | ||