undefined | unit 3 mosfet circuits

Analog Electronic Circuits

Unit 3

MOSFET circuits

Explain the structure of MOSFET ?

MOSFETs are available in two basic forms:

Depletion Type: The transistor requires the Gate-Source voltage (VGS) to switch the device “OFF”. The depletion-mode MOSFET is equivalent to a “Normally Closed” switch.

Enhancement Type: The transistor requires a Gate-Source voltage(VGS) to switch the device “ON”. The enhancement-mode MOSFET is equivalent to a “Normally Open” switch.

Structure:

It is a four-terminal device with source(S), gate (G), drain (D) and body (B) terminals. The body is frequently connected to the source terminal, reducing the terminals to three. It works by varying the width of a channel along which charge carriers flow (electrons or holes).

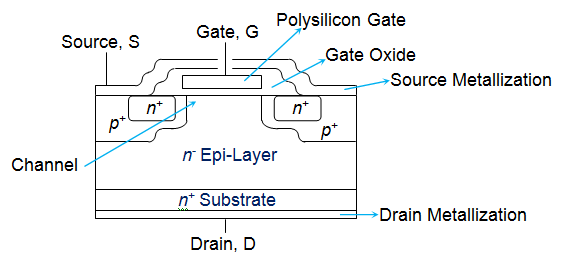
Figure 1. MOSFET has a vertically oriented four-layer structure.

The p-type middle layer term as the body.

The n– layer is the drift layer.

This layer is lightly doped as compared to the drain and source layer.

The breakdown voltage of power MOSFET determines from the width of the drift layer.

First and last both layers are an n+ layer. First layer is the source layer and the last layer is the drain layer.

The charge carriers enter the channel at source and exit via the drain. The width of the channel is controlled by the voltage on an electrode is called gate which is located between source and drain.

A p-channel MOSFET structure has exactly opposite doping profile.

The GATE terminal is not directly connected with p-type, there is an oxide layer between the metal and semiconductor.

This oxide layer act as a dielectric layer between the metal and the semiconductor. It forms a MOS (metal oxide semiconductor) capacitance at the input of the MOSFET.

This capacitance is large (>1000 pF). The oxide layer gives good insulating property by providing the SiO2 layer that isolates the gate terminal from the body layer.

2. Explain the V-I characteristics of MOSFET ?

V-I characteristics

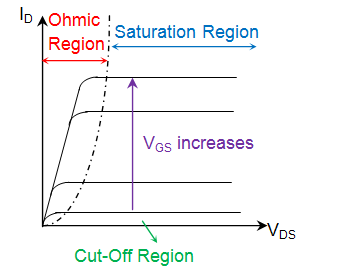
Figure 2. V-I characteristics of MOSFET

It has three regions: saturation, cut-off, and ohmic region.

When the gate-source voltage is less than the threshold voltage, the MOSFET is in the cut-off state. To avoid breakdown the drain to source breakdown voltage should be greater than the applied voltage. The avalanche breakdown takes place.

When the gate-source voltage is greater than threshold the power MOSFET goes into the ohmic region and the drain to source voltage is small. In this region, the power dissipation is low.

In the saturation region, the drain current is almost independent of the drain to source voltage. It is only dependent on the gate to source voltage. The gate voltage is greater than the threshold voltage. The drain current increase with the increase in the gate to source voltage.

3. Explain MOSFET as a switch?

The drain terminal (D) of the MOSFET is connected to the supply voltage VS via the drain resistor RD while its source terminal (S) is grounded. It has an input voltage Vi applied at its gate terminal (G) while the output Vo is drawn from its drain.

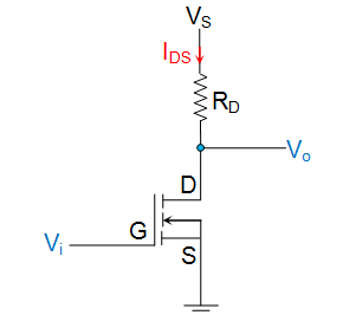
Figure 3. n-channel Enhancement MOSFET functioning as a switch

When Vi = 0V, which means the gate terminal of the MOSFET is left unbiased. As a result, the MOSFET will be OFF and operates in its cut-off region wherein it offers a high impedance path to the flow of current which makes the IDS almost equivalent to zero.

As a result, even the voltage drop across RD will become zero due to which the output voltage Vo will become almost equal to VS.
When Vi > VT under this condition, the MOSFET will start to conduct and if the VS provided is greater than the pinch-off voltage VP of the device then the MOSFET starts to operate in its saturation region.

The device will offer low resistance path for the flow of constant IDS, almost acting like a short circuit. As a result, the output voltage will be pulled towards low voltage level, which will be ideally zero.

Thus, the output voltage alters between VS and zero depending on whether the input provided is less than or greater than VT, respectively. Thus, it can be concluded that MOSFET can be made to function as electronic switches when made to operate between cut-off and saturation operating regions.

4. Explain MOSFET as an amplifier?

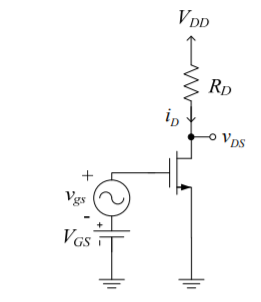
Figure 4. MOSFET as as Amplifier

This is a conceptual amplifier for two resons:

The bias with VGs is impractical.

In ICs large valued resistors take up too much physical space.

To operate as small -signal amplifier we bias MOSFET in saturation region. For analysis of DC operating point we set vgs =0 so that

iD = ½ Kn’ W/L (vgs -Vt) 2 --------------------(1)

From the circuit VDS = VDD – ID RD ------------------------------(2)

For operation in saturation region

vGD ≤ Vt ------ vgs – vds ≤ Vt

or vds ≥ vgs – Vt --------------------------------------------------(3)

where the total drain to source voltage is

vds = Vds + vds

(bias) AC

With an AC signal applied at the gate

Vgs = VGS + vgs -------------------------------(4)

Substituting (4) in (1) we get

iD = ½ kn’ W/L (VGS + vgs – Vt) 2 = ½ kn’ W/L (VGS – Vt) + vgs ] 2 ----------(5)

= ½ kn’ W/L (VGS – Vt) 2 + 2/2 kn ‘ W/L (VGS – Vt) vgs + ½ kn’ W/L v 2 gs ---------(6)

The last term is non linear in vgs which is not desorable for linear amplifier. Hence for linear operation the last term should be small with respect to linear term and the second term is proportional to vgs.

Or vgs<< 2 (VGS – Vt) ------------------------------------------(7)

If this small signal condition (7) is satisfied then from (6) the total drain current is a approximately linear summation.

iD ͌ ID + i d --------------------------------------------------------------(8)

where

id = kn’ W/L (VGS – Vt) vgs ‘ ---------------------------------------(9)

From this expression (9) we see that AC drain current id is related to vgs by transistor transconductance gm.

gm = id / vgs = kn’ W/L (VGS – Vt) [S]

which is sometimes expressed in terms of overdrive voltage VoV = Vgs – Vt

gm = kn’ W/L Vov [S]

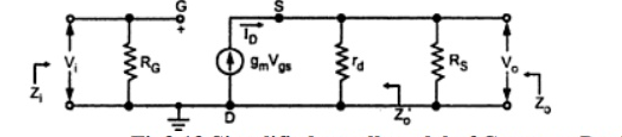
5. Explain small signal model ?

In saturation mode the MOSFET acts as a voltage controlled device . The control voltage is vgs and output current is id which gives rise to small signal model π model.

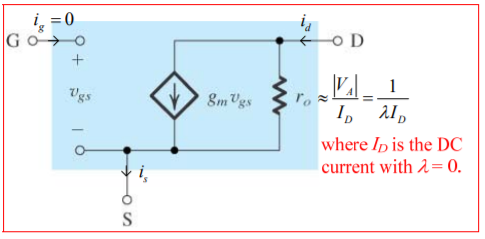
Figure 5. Small signal model of MOSFET

Ig=0 and vgs ≠ 0 the infinite input impedance

ro models the finite output resistance .

We know that gm = k’n W/L (Vgs – Vt)

Hence it can be shown that

gm = 2Id/ Vov = Id / (Vgs – Vt) /2

6.For the circuit shown in figure calculate ID , VDS, VG and VS

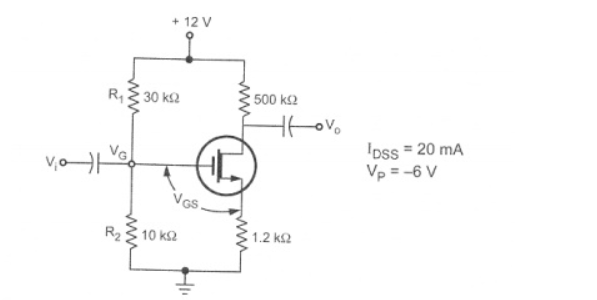
Applying KVL to the input circuit.

VGS = VG – VS

= 3 – IS RS Since VS = IS RS

= 3 – ID RS Since ID = IS

We have

ID = IDSS ( 1 – VGS / VP ) 2

Substituting the value of VGS we get

ID = IDSS ( 1 – (3 – ID RS)/Vp) 2 = 20 x 10 -3 ( 1 – ( 3 – ID x 1.2 x 10 3 / -6)

= 20 x 10 -3 ( 1 – [ (-0.5) + 200 ID ]) 2 = 20 x 10 -3 ( 1.5 -2)

= 20 x 10 -3 (2.25 – 600ID + 40000ID 2)

I D = 0.045 – 12 I D + 800 I D 2

800 I D 2 – 13 I D + 0.045 =0

Solving for quadratic equation we get

= -(-13) ± [ (13) 2 – 4(800)(0.045)] ½ / 2(800)

= 13 ± [ 169 -144] ½ / 1600 = 13 ± 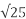/ 1600 = 13 ± 5 /1600 = 5mA or 11.25 mA

If we calculate the value of VDS taking ID = 11.25mA we get

VDS = VDD – ID ( RD + RS)

= 12 – 11.25 x 10 -3 ( 500 + 1.2 x 10 3)

= 12 – 19.125 = -7.125

Practically the value of VDS must be positive hence ID= 11.25 mA is invalid

Hence take ID = 5mA

VDS = VDD – ID (RD + RS) = 12 – 5 x 10 -3 (500 + 1.2 x 10 3) = 12 – 8.5 = 3.5 V

VGS = 3 – ID RS = 3- 5 x 10 -3 x 1.2 x 10 3 = 3 – 6 = -3 V

Vs = ID RS = 5 x 10 -3 x 1.2 x 10 3 = 6V

7.Explain common source amplifier?

Common source amplifier with Voltage divider bias

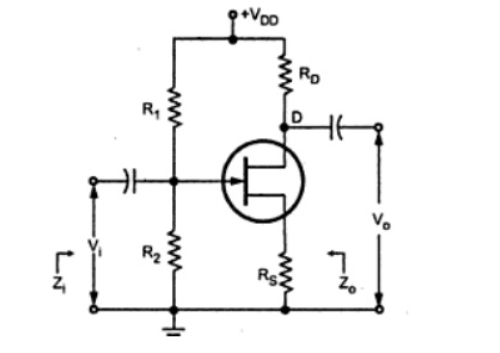
Figure 7. Common Source Amplifier

Now Rs will be the part of low frequency equivalent model as shown in figure.

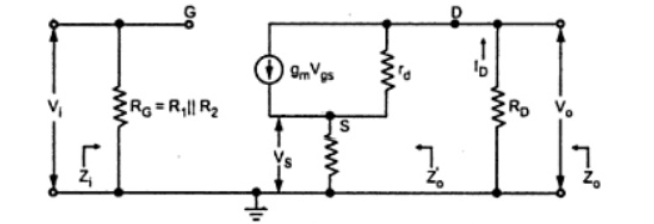
Figure 8. Equivalent model

Note that RG = R1 || R2

Z1 = RG = R1 || R@

Zo’ = rd + gm Rs rd + Rs

Zo’ = rd + Rs ( μ + 1)

Zo = [ rd + gm Rs rd + Rs] || RD

Zo = [ rd + Rs (( μ + 1)] || RD

Av = -gm RD/ 1+ gm Rs + Rs + RD/ rd

8. Explain common gate amplifier?

In this circuit, input is applied between source and gate and output is taken between drain and gate.

Figure 9. Common Gate Amplifier

In CG Configuration, gate potential is at constant potential. so, increase in input voltage Vi in positive direction increase the negative gate source voltage. Due to ID reduces, reduces, reducing the drop IDRD.

Since VD= VDD-IDRD, the reduction in ID results in an increase in output voltage.

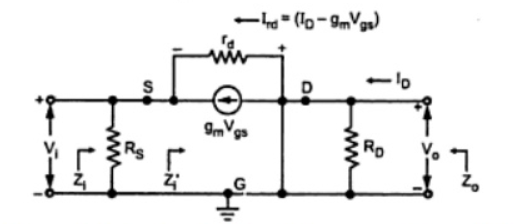
Figure 10. Equivalent model

Input Impedance (Zi)

Zi = Rs || Zi’

And

Zi’ = Vi/I

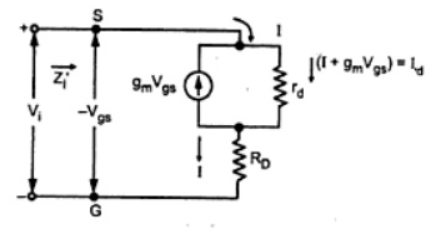
After substituting and simplification,

Vi/I = 1 + RD/rd / 1/rd + gm = rd + RD / 1 + gm rd

Zi = Rs || Zi’ = Rs || rd + RD / 1+gm rd

If rd >> RD and gm rd >> 1 then we can write

Z1 = Rs || rd / gm rd = Rs || 1/gm

Output Impedance

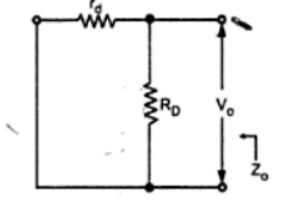
It is given by

Zo = rd || RD

If rd >> RD

Zo = RD

Voltage gain:

Av = Vo/Vi

Vo = - I D R D

Vi = - Vgs

Using KVL to the outer loop after simplication

Av = Vo/ Vi = - Id + RD / -Id ( rd + RD) / 1+ gm rd

If rd >> RD and gmrd >>1

Av = RD (gm rd) / rd = RD gm

9. Explain common drain amplifier ?

In this circuit, input is applied between gate and source and output is taken between source and drain.

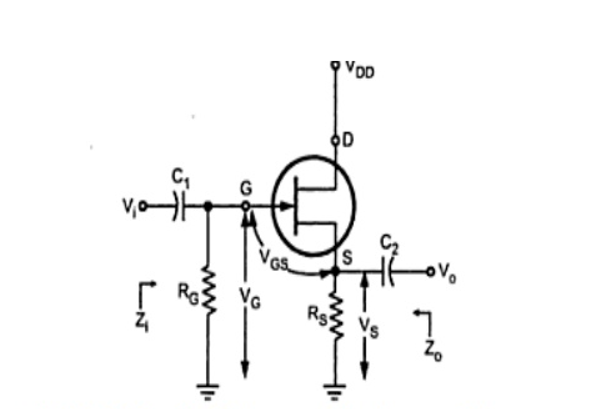
Figure 11. Common Drain Amplifier

In this circuit, the source voltage is

Vs = VG+VGS

When a signal is applied to the JFET gate via C1 ,VG varies with the signal. As VGS is fairly constant and Vs = VG+VGS, Vs varies with Vi.

The following figure shows the low frequency equivalent model for common drain circuit.

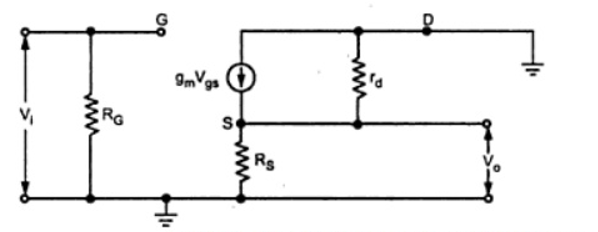
Input Impedance Zi

Zi = RG

Output Impedance Zo

It is given by

Zo = Zo’ || Rs

Where Zo’ = Vo/Id | Vi=0

Applying KVL to the outer loop we have

Vi + Vgs -Vo =0

Vi=0

Looking at the figure we can write

gm Vgs = Id

But Vgs = Vo

gm Vo = Id

Zo’ = Vo/Id = 1/gm

Zo = 1/gm || Rs

Voltage gain (Av)

It is given by

Av = Vo/Vi

Looking at the figure we can write

Vo = -Id (rd|| Rs)

And Id = gm Vgs

Vo = -gm Vgs (rd||Rs)

But

Vi = -Vgs + Vo

= - Vgs + [ -gm Vgs (rd||Rs)

Substitute the value Vo and Vi. Then

Av = -gm vgs (rd||Rs) / -Vgs (1+gm (rd||Rs)

= gm (rd||Rs) / 1+gm (rd || Rs)

If rd >> Rs

Av = gm Rs / 1+ gm Rs

If gm Rs >> 1

Av = 1 but it is always less than one.

Common drain circuit does not provide voltage gain.& there is no phase shift between input and output voltages.

10. Explain small signal equivalent circuits?

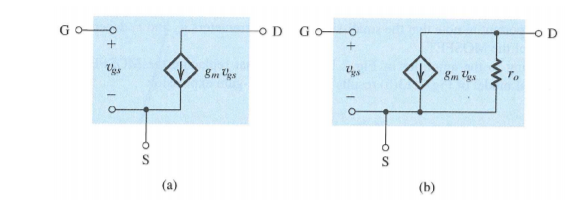
a- Without early affect

b- With early affect

Figure 12. Small signal equivalent circuit

This relationship can be modelled by a current source. Moreover, the gate of the MOSFET is essentially an open circuit at DC. Hence, the small-signal equivalent-circuit model is presented in Figure

When the Early effect has to be accounted for, an output resistor ro can be added as shown in Figure . The value of ro is given as

r o = |VA|/ID where ID = ½ kn V 2 ov

The voltage gain is

Av = vds / vgs = -gm (RD ||ro)

The transconductance is given by

gm = k’n (W/L) (VGS – Vt) = k’n (W/L) VOV = μ n Cox (W/L) VOV

The transconductance can be increased by increasing the W/L ratio, and also increasing the overdrive voltage VOV. But increasing VOV implies that the operating point for VDS has to increase in order for the MOSFET to be in the saturation region. Also, by using the fact that

ID = ½ Kn V2 OV = ½ k’n (W/L) V2 ov

V ov = [ 2ID / k’n (W/L)] ½

gm = [ 2 k’n (W/L) I D ] ½

This implies that gm is proportional to the square roots of the drain current ID, and W/L.

11. Explain high frequency equivalent circuit ?

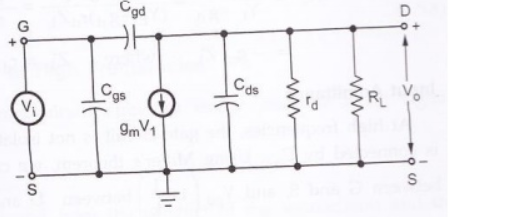
Figure 13. High frequency equivalent circuit.

Y = 1/Z = YL + Yds + gd + Ygd

Where

YL = 1/RL ; admittance corresponding to RL

Yds = jw Cds ; admittance corresponding to Cds

Gd = 1/rd ; conductance corresponding to rd

Ygd = jw Cgd ;admittance corresponding to Cgd.

I = -gm Vi + Vi Ygd = Vi(-gm + Ygd)

Voltage gain:

The voltage gain for common source amplifier circuit with load RL is given by

Av = Vo/Vi = IZ/Vi = 1/ViY

Substituting the values of I nd Y we get

AV = -gm + Ygd/ YL + Yds + gd + Ygd

At low frequencies Yds and Ygd =0 hence

Av = -gm +Ygd/YL + gd = -gm rd ZL/ (YL +gd) rd ZL = -gmrdZL/ rd + ZL

= -gm ZL where ZL = rd ||ZL

Input Admittance :

Yi = Ygs + (1-Av) Ygd

Input capacitance

Av = -gm R’d

Substituting the value of Av

Yi/jw = Ci= Cgs +(1+gmR’d) Cgd

This increase in input capacitance Ci over the capacitance from gate to source is called Miller effect.

This input capacitance affects the gain at high frequencies in the operation of cascaded amplifiers.

In cascaded amplifiers, the output from one stage is used as the input to a second amplifier. The input impedance of a second stage acts as a shunt across output of the first stage and Rd is shunted by the capacitance Ci.

Output Admittance:

The output impedance is obtained by looking into the drain with the input voltage set equal to zero. If Vi = 0 in figure, rd , Cds and Cgd in parallel. Hence the output admittance with RL considered external to the amplifier is given by,

Yo = gd + Yds + Ygd

Sign Up