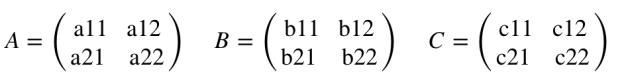undefined | unit 2 introduction to divide and conquer paradigm 1

Design & Analysis of Algorithms

Unit-2Introduction to Divide and Conquer paradigm Q1) What is binary search ?A1) : Binary Search ● It is the searching method where we search an element in the given array● Method starts with the middle element.● if the key element is smaller than the middle element then it searches the key element into first half of the array ie. Left sub-array.● If the key element is greater than the middle element then it searches into the second half of the array ie. Right sub-array.
This process continues until the key element is found. If there is no key element present in the given array then its searches fail. Algorithm Algorithms can be implemented as algorithms that are recursive or non-recursive.

ALGORITHM BinSrch ( A[0 … n-1], key)

//implements non-recursive binary search

//i/p: Array A in ascending order, key k

//o/p: Returns position of the key matched else -1

l 0

r n-1

while l ≤ r do

m ( l + r) / 2

if key = = A[m]

return m

else

if key < A[m]

r m-1

else

l m+1

return -1

Analysis :● Input size: Array size, n ● Basic operation: key comparison● Depend on Best – Matching the key with the middle piece. Worst – Often a key is not identified or a key in the list.● Let C(n) denote the number of times the fundamental operation is performed. Then one, then Cworst t(n)= Performance in worst case. Since the algorithm after each comparison is the issue is divided into half the size we have,Cworst (n) = Cworst (n/2) + 1 for n > 1C(1) = 1● Using the master theorem to solve the recurrence equation, to give the number of when the search key is matched against an element in the list, we have:

C(n) = C(n/2) + 1

a = 1

b = 2

f(n) = n0 ;

d = 0

case 2 holds:

C(n) = Θ (nd log n)

= Θ (n0 log n)

= Θ ( log n)

Application :

Guessing Number game

Word Lists/Dictionary Quest, etc

Limitations :

Interacting badly with the hierarchy of memory

Allows the list to be sorted

Because of the list element's random access, you need arrays instead of a linked list.

Advantages :

Efficient on an incredibly broad list

Iteratively/recursively applied can be

Q2) Define quick sort ?A2) : Quick Sort● Quick sort algorithm works on the pivot element.● Select the pivot element (partitioning element) first. Pivot element can be a random number from a given unsorted array.● Sort the given array according to pivot as the smaller or equal to pivot comes into the left array and greater than or equal to pivot comes into the right array.● Now select the next pivot to divide the elements and sort the sub arrays recursively.
Features ● Developed by C.A.R. Hoare ● Efficient algorithm ● NOT stable sort ● Significantly faster in practice, than other algorithms Algorithm

ALGORITHM Quicksort (A[ l …r ])

//sorts by quick sort

//i/p: A sub-array A[l..r] of A[0..n-1],defined by its left and right indices l and r //o/p: The sub-array A[l..r], sorted in ascending order

if l < r

Partition (A[l..r]) // s is a split position

Quicksort(A[l..s-1])

Quicksort(A[s+1..r]

ALGORITHM Partition (A[l ..r])

//Partitions a sub-array by using its first element as a pivot

//i/p: A sub-array A[l..r] of A[0..n-1], defined by its left and right indices l and r (l <r)

//o/p: A partition of A[l..r], with the split position returned as this function‘s value p→A[l]

i→l

j→r + 1;

Repeat

repeat i→i + 1 until A[i] >=p //left-right scan

repeat j→j – 1 until A[j] < p //right-left scan

if (i < j) //need to continue with the scan

swap(A[i], a[j])

until i >= j //no need to scan

swap(A[l], A[j])

return j

Analysis of Quick Sort Algorithm

Best case: The pivot which we choose will always be swapped into exactly the middle of the list. And also consider pivot will have an equal number of elements both to its left and right sub arrays.

II. Worst case: Assume that the pivot partition the list into two parts, so that one of the partitions has no elements while the other has all the other elements. III. Average case: Assume that the pivot partition the list into two parts, so that one of the partitions has no elements while the other has all the other elements.

Best Case	O (n log n)
Worst Case	O (n2)
Average Case	O (n log n )

Q3) Explain merge sort ?A3) : Merge Sort ● Merge sort consists of two phases as divide and merge.● In the divide phase, each time it divides the given unsorted list into two sublists until each sub list gets a single element then sorts the elements.● In the merge phase, it merges all the solutions of sub lists and finds the original sorted list.Features :● Is an algorithm dependent on comparison?● A stable algorithm is● A fine example of the strategy of divide & conquer algorithm design● John Von Neumann invented it. Steps to solve the problem:Step 1: if the length of the given array is 0 or 1 then it is already sorted, else follow step 2. Step 2: split the given unsorted list into two half partsStep 3: again divide the sub list into two parts until each sub list get single elementStep 4: As each sub list gets the single element compare all the elements with each other & swap in between the elements.Step 5: merge the elements same as divide phase to get the sorted list Algorithm:

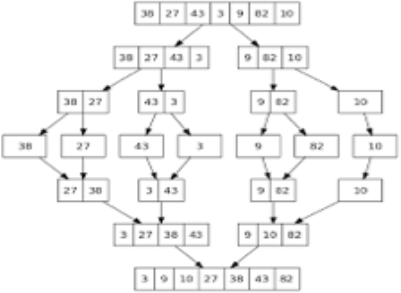
ALGORITHM Mergesort ( A[0… n-1] )

//sorts array A by recursive mergesort

//i/p: array A

//o/p: sorted array A in ascending order

if n > 1

copy A[0… (n/2 -1)] to B[0… (n/2 -1)]

copy A[n/2… n -1)] to C[0… (n/2 -1)]

Mergesort ( B[0… (n/2 -1)] )

Mergesort ( C[0… (n/2 -1)] )

Merge ( B, C, A )

ALGORITHM Merge ( B[0… p-1], C[0… q-1], A[0… p+q-1] )

//merges two sorted arrays into one sorted array

//i/p: arrays B, C, both sorted

//o/p: Sorted array A of elements from B & C

I →0

j→0

k→0

while i < p and j < q do

if B[i] ≤ C[j]

A[k] →B[i]

i→i + 1

else

A[k] →C[j]

j→j + 1

k→k + 1

if i == p

copy C [ j… q-1 ] to A [ k… (p+q-1) ]

else

copy B [ i… p-1 ] to A [ k… (p+q-1) ]

Example :Apply merge sort for the following list of elements: 38, 27, 43, 3, 9, 82, 10

Analysis of merge sort: All cases having same efficiency as: O (n log n) T (n) =T ( n / 2 ) + O ( n )T (1) = 0Space requirement: O (n) Advantages ● The number of comparisons carried out is almost ideal.● Mergesort is never going to degrade to O (n2)● It is applicable to files of any size.Limitations ● Using extra memory O(n). Q4) What do you mean by Strassen’s matrix?A4) : Strassen's MatrixThe standard method of matrix multiplication of two n x n matrices takes T(n) = O(n3). The following algorithm multiplies nxn matrices A and B: // Initialize C.for i = 1 to nfor j = 1 to nfor k = 1 to n C [i, j] += A[i, k] * B[k, j];Strassen’s algorithm is a Divide-and-Conquer algorithm that beats the bound. The usual multiplication of two n x n matrices takes

If C=AB, then we have the following:c11 = a11 b11 + a12 b21c12 = a11 b12 + b12 b22c21 = a21 b11 + a22 b21c22 = a21 b12 + a22 b22 8 n/2 * n/2 matrix multiples plus4 n/2 * n/2 matrix additions T(n) = 8T(n/2) + O(n2)Plug in a = 8, b = 2, k = 2 →logba=3 → T(n)= O(n3)Strassen showed how two matrices can be multiplied using only 7 multiplications and 18 additions:Consider calculating the following 7 products:q1 = (a11 + a22) * (b11 + b22)q2 = (a21 + a22) * b11q3 = a11*( b12 – b22)q4 = a22 * (b21 – b11)q5 = (a11 + a12) * b22q6 = (a21 – a11) * (b11 + b12)q7 = (a12 – a22) * (b21 + b22)It turns out thatc11 = q1 + q4 – q5 + q7c12 = q3 + q5c21 = q2 + q4c22 = q1 + q3 – q2 + q6 Code for Implementation of Strassen’s Matrix Multiplication

#include <assert.h>

#include <stdio.h>

#include <stdlib.h>

#include <time.h>

#define M 2

#define N (1<<M)

typedef double datatype;

#define DATATYPE_FORMAT "%4.2g"

typedefdatatype mat[N][N];

typedefstruct

{

intra, rb, ca, cb;

} corners;

void identity(mat A, corners a)

{

int i, j;

for (i = a.ra; i<a.rb; i++)

for (j = a.ca; j <a.cb; j++)

A[i][j] = (datatype) (i == j);

}

void set(mat A, corners a, datatype k)

{

int i, j;

for (i = a.ra; i<a.rb; i++)

for (j = a.ca; j <a.cb; j++)

A[i][j] = k;

}

voidrandk(mat A, corners a, double l, double h)

{

int i, j;

for (i = a.ra; i<a.rb; i++)

for (j = a.ca; j <a.cb; j++)

A[i][j] = (datatype) (l + (h - l) * (rand() / (double) RAND_MAX));

}

void print(mat A, corners a, char *name)

{

int i, j;

printf("%s = {\n", name);

for (i = a.ra; i<a.rb; i++)

{

for (j = a.ca; j <a.cb; j++)

printf(DATATYPE_FORMAT ", ", A[i][j]);

printf("\n");

}

printf("}\n");

}

void add(mat A, mat B, mat C, corners a, corners b, corners c)

{

intrd = a.rb - a.ra;

int cd = a.cb - a.ca;

int i, j;

for (i = 0; i<rd; i++)

{

for (j = 0; j < cd; j++)

{

C[i + c.ra][j + c.ca] = A[i + a.ra][j + a.ca] + B[i + b.ra][j

+ b.ca];

}

void sub(mat A, mat B, mat C, corners a, corners b, corners c)

{

intrd = a.rb - a.ra;

int cd = a.cb - a.ca;

int i, j;

for (i = 0; i<rd; i++)

{

for (j = 0; j < cd; j++)

{

C[i + c.ra][j + c.ca] = A[i + a.ra][j + a.ca] - B[i + b.ra][j

+ b.ca];

} }

}

voidfind_corner(corners a, inti, int j, corners *b)

{

intrm = a.ra + (a.rb - a.ra) / 2;

int cm = a.ca + (a.cb - a.ca) / 2;

*b = a;

if (i == 0)

b->rb = rm;

else

b->ra = rm;

if (j == 0)

b->cb = cm;

else

b->ca = cm;

}

voidmul(mat A, mat B, mat C, corners a, corners b, corners c)

{

cornersaii[2][2], bii[2][2], cii[2][2], p;

mat P[7], S, T;

int i, j, m, n, k;

m = a.rb - a.ra;

assert(m==(c.rb-c.ra));

n = a.cb - a.ca;

assert(n==(b.rb-b.ra));

k = b.cb - b.ca;

assert(k==(c.cb-c.ca));

assert(m>0);

if (n == 1)

{

C[c.ra][c.ca] += A[a.ra][a.ca] * B[b.ra][b.ca];

return;

}

for (i = 0; i < 2; i++)

{

for (j = 0; j < 2; j++)

{

find_corner(a, i, j, &aii[i][j]);

find_corner(b, i, j, &bii[i][j]);

find_corner(c, i, j, &cii[i][j]);

}

p.ra = p.ca = 0;

p.rb = p.cb = m / 2;

#define LEN(A) (sizeof(A)/sizeof(A[0]))

for (i = 0; i < LEN(P); i++)

set(P[i], p, 0);

#define ST0 set(S,p,0); set(T,p,0)

ST0;

add(A, A, S, aii[0][0], aii[1][1], p);

add(B, B, T, bii[0][0], bii[1][1], p);

mul(S, T, P[0], p, p, p);

ST0;

add(A, A, S, aii[1][0], aii[1][1], p);

mul(S, B, P[1], p, bii[0][0], p);

ST0;

sub(B, B, T, bii[0][1], bii[1][1], p);

mul(A, T, P[2], aii[0][0], p, p);

ST0;

sub(B, B, T, bii[1][0], bii[0][0], p);

mul(A, T, P[3], aii[1][1], p, p);

ST0;

add(A, A, S, aii[0][0], aii[0][1], p);

mul(S, B, P[4], p, bii[1][1], p);

ST0;

sub(A, A, S, aii[1][0], aii[0][0], p);

add(B, B, T, bii[0][0], bii[0][1], p);

mul(S, T, P[5], p, p, p);

ST0;

sub(A, A, S, aii[0][1], aii[1][1], p);

add(B, B, T, bii[1][0], bii[1][1], p);

mul(S, T, P[6], p, p, p);

add(P[0], P[3], S, p, p, p);

sub(S, P[4], T, p, p, p);

add(T, P[6], C, p, p, cii[0][0]);

add(P[2], P[4], C, p, p, cii[0][1]);

add(P[1], P[3], C, p, p, cii[1][0]);

add(P[0], P[2], S, p, p, p);

sub(S, P[1], T, p, p, p);

add(T, P[5], C, p, p, cii[1][1])

}

int main()

{

mat A, B, C;

cornersai = { 0, N, 0, N };

corners bi = { 0, N, 0, N };

corners ci = { 0, N, 0, N };

srand(time(0));

randk(A, ai, 0, 2);

randk(B, bi, 0, 2);

print(A, ai, "A");

print(B, bi, "B");

set(C, ci, 0);

mul(A, B, C, ai, bi, ci);

print(C, ci, "C");

return 0

}

Q5) Describe Karatsuba algorithm for fast multiplications?A5) : Karatsuba Algorithm for Fast Multiplication A fast multiplication algorithm that uses a divide and conquer approach to multiply two numbers is the Karatsuba algorithm. Anatoly Karatsuba discovered it in 1960 and published it in 1962. Given two binary strings representing the value of two integers, find the two string product. For example, the output should be 120 if the first bit string is "1100" and the second bit string is "1010".For simplicity, let the length be the same for two strings and be n. One by one, take all bits of the second number and multiply it with all bits of the first number in the naive method. Finally, all multiplications are added. This algorithm takes O(n^2) time. Using Divide and Conquer, with less time complexity, we can multiply two integers. We divide the numbers given into two halves. Let X and Y be the numbers given. Let us assume for simplicity that n is evenXl*2n/2 + Xr [Xl and Xr contain n/2 bits of X on the leftmost and rightmost]Yl*2n/2 + Yr [Yl and Yr contain n/2 bits of Y on the leftmost and rightmost] The product XY can be written as the following :

XY = (Xl*2n/2 + Xr)(Yl*2n/2 + Yr)

= 2n XlYl + 2n/2(XlYr + XrYl) + XrYr

There are four multiplications of size n/2 if we take a look at the above formula, so we basically divided the size n problem into four subproblems of size n/2. But that does not help, because T(n) = 4T(n/2) + O(n) recurrence solution is O(n^2). The difficult part of this algorithm is to change the middle two terms to some other form so that it would be sufficient for only one extra multiplication.For the middle two terms, the following is a tricky expression XlYr + XrYl = (Xl + Xr)(Yl + Yr) - XlYl- XrYr In this way, the final value of XY becomesXY = 2n XlYl + 2n/2 * [(Xl + Xr)(Yl + Yr) - XlYl - XrYr] + XrYr The recurrence becomes T(n) = 3T(n/2) + O(n) with the above trick and O(n) is the solution to this recurrence O(n1.59 ). What if the input string lengths are different and they are not even? We attach 0's at the beginning to accommodate the different length case. We put floor(n/2) bits in the left half and ceil(n/2) bits in the right half to manage the odd length. So the XY expression switches to the following one. The algorithm above is referred to as the Karatsuba algorithm and can be used on any basis.XY = 22ceil(n/2) XlYl + 2ceil(n/2) * [(Xl + Xr)(Yl + Yr) - XlYl - XrYr] + XrYr Application :● In tasks that involve integer multiplication, the Karatsuba algorithm is very effective. For polynomial multiplications, it may also be useful. ● It is to be remembered that algorithms for faster multiplication exist. Q6) Write about max and min heap ?A6) : Max and Min HeapHeap is the special tree based data structure in which it has to satisfy the condition of a complete binary tree.Following are two types of heap:Max-heap: In this key present at root node must be greater among all key present at all of its children.A [PARENT (i) ≥A[i] For all the sub-trees in that binary tree, the same property must be recursively valid. The minimum main factor present at the root is present in a Min-Heap. Below is the binary tree that satisfies all of Min Heap's assets.Min-heap: In this key present at root node must be minimum among all key present at all of its children.A [PARENT (i) ≤A[i]For all the sub-trees in that binary tree, the same property must be recursively valid. The maximum main factor present at the root is in the Max-Heap. Below is the binary tree that satisfies all of Min Heap's assets.

Fig 1: min and max heap Q7) What do you mean by heap sort?A7) : Heap SortHeap Sort is one of the best in-place sorting strategies with no worst-case quadratic runtime. Heap sort requires the creation of a Heap data structure from the specified array and then the use of the Heap to sort the array. You should be wondering how it can help to sort the array by converting an array of numbers into a heap data structure. To understand this, let's begin by knowing what a heap is. Heap is a unique tree-based data structure that meets the following special heap characteristics:

Shape property : The structure of Heap data is always a Complete Binary Tree, which means that all tree levels are fully filled.

2. Heap property : Every node is either greater or equal to, or less than, or equal to, each of its children. If the parent nodes are larger than their child nodes, the heap is called Max-Heap, and the heap is called Min-Heap if the parent nodes are smaller than their child nodes. The Heap sorting algorithm is split into two basic components: ● Creating an unsorted list/array heap.● By repeatedly removing the largest/smallest element from the heap, and inserting it into the array, a sorted array is then created. Complexity analysis of heap sortTime complexity :● Worst case : O(n*log n)● Best case : O(n*log n)● Average case : O(n*log n) Space complexity : O(1) Q8) Write any example of binary search ?A8) : Example of Binary Search Let us explain the following 9 elements of binary search:

The number of comparisons required to check for various components is as follows: 1. Searching for x = 101 low high mid 1 9 5 6 9 7 8 9 8 9 9 9 Found Number of comparison : 4 2. Searching for x = 82 low high mid 1 9 5 6 9 7 8 9 8 Found Number of comparison : 3 3. Searching for x = 42 low high mid 1 9 5 6 9 7 6 6 6 7 6 not Found Number of comparison : 4 4. Searching for x = -14 low high mid 1 9 5 1 4 2 1 1 1 2 1 not Found Number of comparison : 3 The number of element comparisons required to find each of the nine elements continues in this manner:

Index	1	2	3	4	5	6	7	8	9
Elements	-1	-6	0	7	9	23	54	82	10
Comparison	3	2	3	4	1	3	2	3	4

No part needs seeking more than 4 comparisons. Summarizing theComparisons were required for all nine things to be identified and divided by 9, yielding 25/9 . On average, there are around 2.77 comparisons per effective quest. Depending on the value of x, there are ten possible ways that an un-successful quest will end. If x < a[1], a[1] < x < a[2], a[2] < x < a[3], a[5] < x < a[6], a[6] < x < a[7] or a[7] < x < a[8] The algorithm requires 3 comparisons of components to decide the 'x'This isn't present. Binsrch needs 4 part comparisons for all of the remaining choices. Thus, the average number of comparisons of elements for a failed search is: (3 + 3 + 3 + 4 + 4 + 3 + 3 + 3 + 4 + 4) / 10 = 34/10 =3.4 The time complexity for a successful search is O(log n) and for an unsuccessful search is Θ(log n). Q9) Write the difference between max and min heap ?A9) : Difference between Max and Min Heap

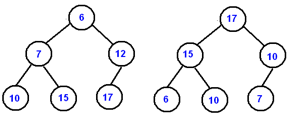
Min Heap	Max Heap
The key present at the root node in a Min-Heap must be less than or equal to one of the keys present in all of its children.	The key present at the root node in a Max-Heap must be greater than or equal to one of the keys present in all of its children.
The minimum main factor present at the root is present in a Min-Heap.	The maximum main factor present at the root is in the Max-Heap.
The ascending priority is used by A Min-Heap.	The descending priority is used by the Max-Heap.
The smallest component has priority in the design of a Min-Heap.	In the construction of a Max-Heap, priority is given to the largest element.
The smallest item in a Min-Heap is the first to pop from the heap.	In a Max-Heap, the first to pop from the heap is the largest element.

Q10) What is the build heap ?A10) : Build Heap BUILDHEAP (array A, int n) for i ← n/2 down to 1 do HEAPIFY (A, i, n) Heap-Sort Algorithm HEAP-SORT (A)BUILD-MAX-HEAP (A)For I ← length[A] down to ZDo exchange A [1] ←→ A [i]Heap-size [A] ← heap-size [A]-1MAX-HEAPIFY (A,1) Analysis :Building a max-heap requires O(n) run time. The Heap Sort algorithm makes a call to 'Construct Max-Heap' that we use to address a new heap with O(n) time & each of the (n-1) calls to Max-heap. We know it takes time to 'Max-Heapify' O (log n).The total running time of Heap-Sort is O (n log n).

Sign Up