Design & Analysis of Algorithms
UNIT-3Overview of Brute-Force Q1) What is Brute force attack and what are its types?A1)Brute Force AttackA Brute force attack is a well-known breaking technique, by certain records, brute force attacks represented five percent of affirmed security ruptures. A brute force attack includes ‘speculating’ username and passwords to increase unapproved access to a framework. Brute force is a straightforward attack strategy and has a high achievement rate.A few attackers use applications and contents as brute force devices. These instruments evaluate various secret word mixes to sidestep confirmation forms. In different cases, attackers attempt to get to web applications via scanning for the correct session ID. Attacker inspiration may incorporate taking data, contaminating destinations with malware, or disturbing help. While a few attackers still perform brute force attacks physically, today practically all brute force attacks are performed by bots. Attackers have arrangements of usually utilized accreditations, or genuine client qualifications, got through security breaks or the dull web. Bots deliberately attack sites and attempt these arrangements of accreditations, and advise the attacker when they obtain entrance.Types of Brute Force Attacks:Dictionary attacks – surmises usernames or passwords utilizing a dictionary of potential strings or phrases. Rainbow table attacks – a rainbow table is a precomputed table for turning around cryptographic hash capacities. It very well may be utilized to figure a capacity up to a specific length comprising of a constrained arrangement of characters. Reverse brute force attack – utilizes a typical password or assortment of passwords against numerous conceivable usernames. Focuses on a network of clients for which the attackers have recently acquired information. Hybrid brute force attacks – begins from outer rationale to figure out which password variety might be destined to succeed, and afterward proceeds with the simple way to deal with attempt numerous potential varieties. Simple brute force attack – utilizes an efficient way to deal with ‘surmise’ that doesn’t depend on outside rationale. Credential stuffing – utilizes beforehand known password-username sets, attempting them against numerous sites. Adventures the way that numerous clients have the equivalent username and password across various frameworks. Q2) How to Prevent Brute Force Password Hacking?A2)
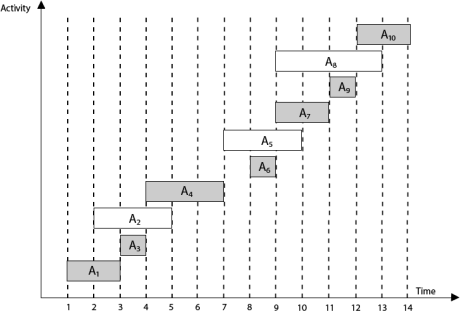
To protect your organization from brute force password hacking, enforce the use of strong passwords.Passwords should:Never use information that can be found online (like names of family members). Have as many characters as possible. Combine letters, numbers, and symbols. Avoid common patterns. Be different for each user account. Change your password periodically Use strong and long password Use multifactor authentication Q3) What is Greedy Programming method?A3)"Greedy Method finds out of many options, but you have to choose the best option."In this method, we have to find out the best method/option out of many present ways.In this approach/method we focus on the first stage and decide the output, don't think about the future. This method may or may not give the best output.Greedy Algorithm solves problems by making the best choice that seems best at the particular moment. Many optimization problems can be determined using a greedy algorithm. Some issues have no efficient solution, but a greedy algorithm may provide a solution that is close to optimal. A greedy algorithm works if a problem exhibits the following two properties:Greedy Choice Property: A globally optimal solution can be reached at by creating a locally optimal solution. In other words, an optimal solution can be obtained by creating "greedy" choices. Optimal substructure: Optimal solutions contain optimal subsolutions. In other words, answers to subproblems of an optimal solution are optimal. Example:machine scheduling Fractional Knapsack Problem Minimum Spanning Tree Huffman Code Job Sequencing Activity Selection Problem Steps for achieving a Greedy Algorithm are:Feasible: Here we check whether it satisfies all possible constraints or not, to obtain at least one solution to our problems. Local Optimal Choice: In this, the choice should be the optimum which is selected from the currently available Unalterable: Once the decision is made, at any subsequence step that option is not altered. Q4) Write an Algorithm of Greedy- Activity Selector with exampleA4) GREEDY- ACTIVITY SELECTOR (s, f)1. n ← length [s]2. A ← {1}3. j ← 1.4. for i ← 2 to n5. do if si ≥ fi6. then A ← A ∪ {i}7. j ← i8. return AExample: Given 10 activities along with their start and end time asS = (A1 A2 A3 A4 A5 A6 A7 A8 A9 A10)Si = (1,2,3,4,7,8,9,9,11,12)fi = (3,5,4,7,10,9,11,13,12,14)Compute a schedule where the greatest number of activities takes place.Solution: The solution to the above Activity scheduling problem using a greedy strategy is illustrated below:Arranging the activities in increasing order of end time
Now, schedule A1Next schedule A3 as A1 and A3 are non-interfering.Next skip A2 as it is interfering.Next, schedule A4 as A1 A3 and A4 are non-interfering, then next, schedule A6 as A1 A3 A4 and A6 are non-interfering.Skip A5 as it is interfering.Next, schedule A7 as A1 A3 A4 A6 and A7 are non-interfering.Next, schedule A9 as A1 A3 A4 A6 A7 and A9 are non-interfering.Skip A8 as it is interfering.Next, schedule A10 as A1 A3 A4 A6 A7 A9 and A10 are non-interfering.Thus the final Activity schedule is:
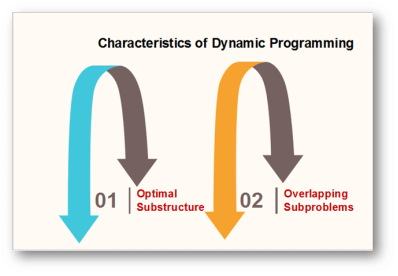
Q5) What is dynamic programming and what are its characteristics, elements and components? A5) Dynamic Programming is the most powerful design technique for solving optimization problems.Divide & Conquer algorithm partition the problem into disjoint subproblems solve the subproblems recursively and then combine their solution to solve the original problems.Dynamic Programming is used when the subproblems are not independent, e.g. when they share the same subproblems. In this case, divide and conquer may do more work than necessary, because it solves the same sub problem multiple times.Dynamic Programming solves each subproblems just once and stores the result in a table so that it can be repeatedly retrieved if needed again.Dynamic Programming is a Bottom-up approach- we solve all possible small problems and then combine to obtain solutions for bigger problems.Dynamic Programming is a paradigm of algorithm design in which an optimization problem is solved by a combination of achieving sub-problem solutions and appearing to the "principle of optimality".Characteristics of Dynamic Programming:Dynamic Programming works when a problem has the following features:-
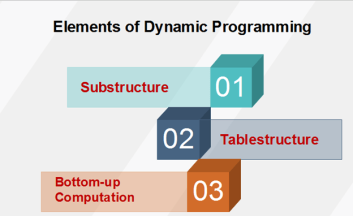
Fig 1 - Characteristics of Dynamic ProgrammingOptimal Substructure: If an optimal solution contains optimal sub solutions then a problem exhibits optimal substructure. Overlapping subproblems: When a recursive algorithm would visit the same subproblems repeatedly, then a problem has overlapping subproblems. If a problem has optimal substructure, then we can recursively define an optimal solution. If a problem has overlapping subproblems, then we can improve on a recursive implementation by computing each subproblem only once.If a problem doesn't have optimal substructure, there is no basis for defining a recursive algorithm to find the optimal solutions. If a problem doesn't have overlapping sub problems, we don't have anything to gain by using dynamic programming.If the space of subproblems is enough (i.e. polynomial in the size of the input), dynamic programming can be much more efficient than recursion.Elements of Dynamic ProgrammingThere are basically three elements that characterize a dynamic programming algorithm:-
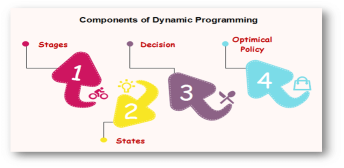
Fig 2 - Elements of Dynamic ProgrammingSubstructure: Decompose the given problem into smaller subproblems. Express the solution of the original problem in terms of the solution for smaller problems. Table Structure: After solving the sub-problems, store the results to the sub problems in a table. This is done because subproblem solutions are reused many times, and we do not want to repeatedly solve the same problem over and over again. Bottom-up Computation: Using table, combine the solution of smaller subproblems to solve larger subproblems and eventually arrives at a solution to complete problem. Note: Bottom-up means:-Start with smallest subproblems. Combining their solutions obtain the solution to sub-problems of increasing size. Until solving at the solution of the original problem. Components of Dynamic programming
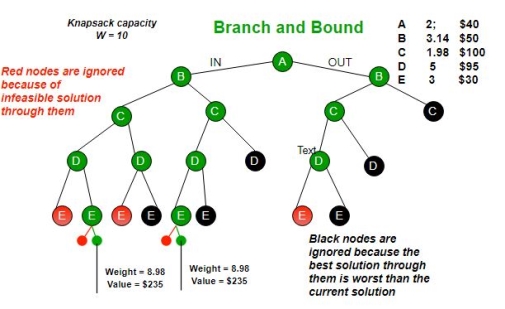
Fig 3 - Components of Dynamic programmingStages: The problem can be divided into several subproblems, which are called stages. A stage is a small portion of a given problem. For example, in the shortest path problem, they were defined by the structure of the graph. States: Each stage has several states associated with it. The states for the shortest path problem was the node reached. Decision: At each stage, there can be multiple choices out of which one of the best decisions should be taken. The decision taken at every stage should be optimal; this is called a stage decision. Optimal policy: It is a rule which determines the decision at each stage; a policy is called an optimal policy if it is globally optimal. This is known as Bellman principle of optimality. Given the current state, the optimal choices for each of the remaining states does not depend on the previous states or decisions. In the shortest path problem, it was not necessary to know how we got a node only that we did. There exist a recursive relationship that identify the optimal decisions for stage j, given that stage j+1, has already been solved. The final stage must be solved by itself. Q6) Write the development of dynamic programming algorithm and its applicationA6) Development of Dynamic Programming AlgorithmIt can be broken into four steps:Characterize the structure of an optimal solution. Recursively defined the value of the optimal solution. Like Divide and Conquer, divide the problem into two or more optimal parts recursively. This helps to determine what the solution will look like. Compute the value of the optimal solution from the bottom up (starting with the smallest subproblems) Construct the optimal solution for the entire problem form the computed values of smaller subproblems. Applications of dynamic programming0/1 knapsack problem Mathematical optimization problem All pair Shortest path problem Reliability design problem Longest common subsequence (LCS) Flight control and robotics control Time-sharing: It schedules the job to maximize CPU usage Q7) Explain Branch and Bound and back tracking methodologiesA7) Branch and bound is an algorithm design paradigm which is generally used for solving combinatorial optimization problems. These problems are typically exponential in terms of time complexity and may require exploring all possible permutations in worst case. The Branch and Bound Algorithm technique solves these problems relatively quickly.Let us consider the 0/1 Knapsack problem to understand Branch and Bound.There are many algorithms by which the knapsack problem can be solved:Greedy Algorithm for Fractional KnapsackDP solution for 0/1 KnapsackBacktracking Solution for 0/1 Knapsack.Let’s see the Branch and Bound Approach to solve the 0/1 Knapsack problem: The Backtracking Solution can be optimized if we know a bound on best possible solution subtree rooted with every node. If the best in subtree is worse than current best, we can simply ignore this node and its subtrees. So we compute bound (best solution) for every node and compare the bound with current best solution before exploring the node.Example bounds used in below diagram are, A down can give $315, B down can $275, C down can $225, D down can $125 and E down can $30.
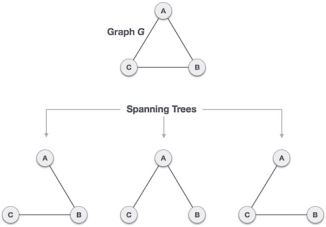
Q8) Explain in detail Minimum Cost Spanning TreeA8) A spanning tree is a subset of Graph G, which has all the vertices covered with minimum possible number of edges. Hence, a spanning tree does not have cycles and it cannot be disconnected..By this definition, we can draw a conclusion that every connected and undirected Graph G has at least one spanning tree. A disconnected graph does not have any spanning tree, as it cannot be spanned to all its vertices.
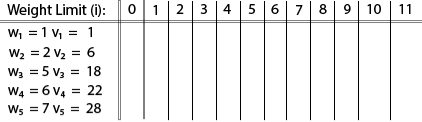
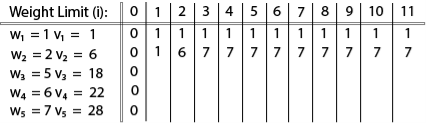
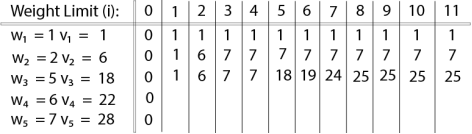
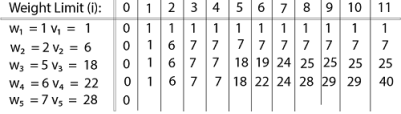
Fig 6 – Spanning TreeWe found three spanning trees off one complete graph. A complete undirected graph can have maximum nn-2 number of spanning trees, where n is the number of nodes. In the above addressed example, n is 3, hence 33−2 = 3 spanning trees are possible.General Properties of Spanning TreeWe now understand that one graph can have more than one spanning tree. Following are a few properties of the spanning tree connected to graph G −A connected graph G can have more than one spanning tree. All possible spanning trees of graph G, have the same number of edges and vertices. The spanning tree does not have any cycle (loops). Removing one edge from the spanning tree will make the graph disconnected, i.e. the spanning tree is minimally connected. Adding one edge to the spanning tree will create a circuit or loop, i.e. the spanning tree is maximally acyclic. Mathematical Properties of Spanning TreeSpanning tree has n-1 edges, where n is the number of nodes (vertices). From a complete graph, by removing maximum e - n + 1 edges, we can construct a spanning tree. A complete graph can have maximum nn-2 number of spanning trees. Thus, we can conclude that spanning trees are a subset of connected Graph G and disconnected graphs do not have spanning tree.Application of Spanning TreeSpanning tree is basically used to find a minimum path to connect all nodes in a graph. Common application of spanning trees are −Civil Network Planning Computer Network Routing Protocol Cluster Analysis Let us understand this through a small example. Consider, city network as a huge graph and now plans to deploy telephone lines in such a way that in minimum lines we can connect to all city nodes. This is where the spanning tree comes into picture.Minimum Spanning Tree (MST)In a weighted graph, a minimum spanning tree is a spanning tree that has minimum weight than all other spanning trees of the same graph. In real-world situations, this weight can be measured as distance, congestion, traffic load or any arbitrary value denoted to the edges.Minimum Spanning-Tree AlgorithmWe shall learn about two most important spanning tree algorithms here −Kruskal's Algorithm Prim's Algorithm Both are greedy algorithms. Q9) Explain in detail Knapsack problem with example and write algorithm alsoA9) Knapsack is basically means bag. A bag of given capacity.We want to pack n items in your luggage.The ith item is worth vi dollars and weight wi pounds. Take as valuable a load as possible, but cannot exceed W pounds. vi wi W are integers. W ≤ capacity Value ← Max Input:Knapsack of capacity List (Array) of weight and their corresponding value. Output: To maximize profit and minimize weight in capacity.The knapsack problem where we have to pack the knapsack with maximum value in such a manner that the total weight of the items should not be greater than the capacity of the knapsack.Knapsack problem can be further divided into two parts: 1. Fractional Knapsack: Fractional knapsack problem can be solved by Greedy Strategy where as 0 /1 problem is not. It cannot be solved by Dynamic Programming Approach.0/1 Knapsack Problem:In this item cannot be broken which means thief should take the item as a whole or should leave it. That's why it is called 0/1 knapsack Problem.Each item is taken or not taken. Cannot take a fractional amount of an item taken or take an item more than once. It cannot be solved by the Greedy Approach because it is enable to fill the knapsack to capacity. Greedy Approach doesn't ensure an Optimal Solution. Example of 0/1 Knapsack Problem:Example: The maximum weight the knapsack can hold is W is 11. There are five items to choose from. Their weights and values are presented in the following table:
The [i, j] entry here will be V [i, j], the best value obtainable using the first "i" rows of items if the maximum capacity were j. We begin by initialization and first row.
V [i, j] = max {V [i - 1, j], vi + V [i - 1, j -wi]
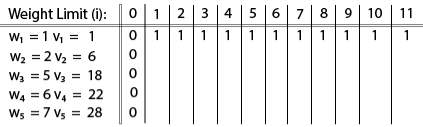
The maximum value of items in the knapsack is 40, the bottom-right entry). The dynamic programming approach can now be coded as the following algorithm:Algorithm of Knapsack ProblemKNAPSACK (n, W) 1. for w = 0, W 2. do V [0,w] ← 0 3. for i=0, n 4. do V [i, 0] ← 0 5. for w = 0, W 6. do if (wi≤ w & vi + V [i-1, w - wi]> V [i -1,W]) 7. then V [i, W] ← vi + V [i - 1, w - wi] 8. else V [i, W] ← V [i - 1, w] Q10) What is Job Sequencing Problem explain with examples?A10) Problem StatementIn job sequencing problem, the objective is to find a sequence of jobs, which is completSed within their deadlines and gives maximum profit.SolutionLet us consider, a set of n given jobs which are associated with deadlines and profit is earned, if a job is completed by its deadline. These jobs need to be ordered in such a way that there is maximum profit.It may happen that all of the given jobs may not be completed within their deadlines.Assume, deadline of ith job Ji is di and the profit received from this job is pi. Hence, the optimal solution of this algorithm is a feasible solution with maximum profit.Thus, D(i)>0for 1⩽i⩽nInitially, these jobs are ordered according to profit, i.e. p1⩾p2⩾p3⩾...⩾pnAlgorithm: Job-Sequencing-With-Deadline (D, J, n, k) D(0) := J(0) := 0 k := 1 J(1) := 1 // means first job is selected for i = 2 … n do r := k while D(J(r)) > D(i) and D(J(r)) ≠ r do r := r – 1 if D(J(r)) ≤ D(i) and D(i) > r then for l = k … r + 1 by -1 do J(l + 1) := J(l) J(r + 1) := i k := k + 1 AnalysisIn this algorithm, we are using two loops, one is within another. Hence, the complexity of this algorithm is O(n2)ExampleLet us consider a set of given jobs as shown in the following table. We have to find a sequence of jobs, which will be completed within their deadlines and will give maximum profit. Each job is associated with a deadline and profit.
SolutionTo solve this problem, the given jobs are sorted according to their profit in a descending order. Hence, after sorting, the jobs are ordered as shown in the following table.
From this set of jobs, first we select J2, as it can be completed within its deadline and contributes maximum profit.Next, J1 is selected as it gives more profit compared to J4. In the next clock, J4 cannot be selected as its deadline is over, hence J3 is selected as it executes within its deadline. The job J5 is discarded as it cannot be executed within its deadline. Thus, the solution is the sequence of jobs (J2, J1, J3), which are being executed within their deadline and gives maximum profit.Total profit of this sequence is 100 + 60 + 20 = 180.
To protect your organization from brute force password hacking, enforce the use of strong passwords.Passwords should:
|
Now, schedule A1Next schedule A3 as A1 and A3 are non-interfering.Next skip A2 as it is interfering.Next, schedule A4 as A1 A3 and A4 are non-interfering, then next, schedule A6 as A1 A3 A4 and A6 are non-interfering.Skip A5 as it is interfering.Next, schedule A7 as A1 A3 A4 A6 and A7 are non-interfering.Next, schedule A9 as A1 A3 A4 A6 A7 and A9 are non-interfering.Skip A8 as it is interfering.Next, schedule A10 as A1 A3 A4 A6 A7 A9 and A10 are non-interfering.Thus the final Activity schedule is:
|
|
|
|
|
|
|
|
The value of V [3, 7] was computed as follows: V [3, 7] = max {V [3 - 1, 7], v3 + V [3 - 1, 7 - w3] = max {V [2, 7], 18 + V [2, 7 - 5]} = max {7, 18 + 6} = 24
Finally, the output is:
|
The maximum value of items in the knapsack is 40, the bottom-right entry). The dynamic programming approach can now be coded as the following algorithm:Algorithm of Knapsack ProblemKNAPSACK (n, W) 1. for w = 0, W 2. do V [0,w] ← 0 3. for i=0, n 4. do V [i, 0] ← 0 5. for w = 0, W 6. do if (wi≤ w & vi + V [i-1, w - wi]> V [i -1,W]) 7. then V [i, W] ← vi + V [i - 1, w - wi] 8. else V [i, W] ← V [i - 1, w] Q10) What is Job Sequencing Problem explain with examples?A10) Problem StatementIn job sequencing problem, the objective is to find a sequence of jobs, which is completSed within their deadlines and gives maximum profit.SolutionLet us consider, a set of n given jobs which are associated with deadlines and profit is earned, if a job is completed by its deadline. These jobs need to be ordered in such a way that there is maximum profit.It may happen that all of the given jobs may not be completed within their deadlines.Assume, deadline of ith job Ji is di and the profit received from this job is pi. Hence, the optimal solution of this algorithm is a feasible solution with maximum profit.Thus, D(i)>0for 1⩽i⩽nInitially, these jobs are ordered according to profit, i.e. p1⩾p2⩾p3⩾...⩾pnAlgorithm: Job-Sequencing-With-Deadline (D, J, n, k) D(0) := J(0) := 0 k := 1 J(1) := 1 // means first job is selected for i = 2 … n do r := k while D(J(r)) > D(i) and D(J(r)) ≠ r do r := r – 1 if D(J(r)) ≤ D(i) and D(i) > r then for l = k … r + 1 by -1 do J(l + 1) := J(l) J(r + 1) := i k := k + 1 AnalysisIn this algorithm, we are using two loops, one is within another. Hence, the complexity of this algorithm is O(n2)ExampleLet us consider a set of given jobs as shown in the following table. We have to find a sequence of jobs, which will be completed within their deadlines and will give maximum profit. Each job is associated with a deadline and profit.
Job | J1 | J2 | J3 | J4 | J5 |
Deadline | 2 | 1 | 3 | 2 | 1 |
Profit | 60 | 100 | 20 | 40 | 20 |
Job | J2 | J1 | J4 | J3 | J5 |
Deadline | 1 | 2 | 2 | 3 | 1 |
Profit | 100 | 60 | 40 | 20 | 20 |
0 matching results found