SN

Traversal

Description

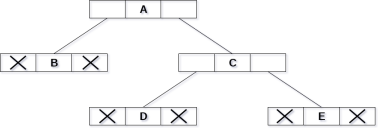
1

Pre-order Traversal

Traverse the root first then traverse into the left sub-tree and right sub-tree respectively. This procedure will be applied to each sub-tree of the tree recursively.

2

In-order Traversal

Traverse the left sub-tree first, and then traverse the root and the right sub-tree respectively. This procedure will be applied to each sub-tree of the tree recursively.

3

Post-order Traversal

Traverse the left sub-tree and then traverse the right sub-tree and root respectively. This procedure will be applied to each sub-tree of the tree recursively.

#include<bits/stdc++.h>

using namespace std;

// An expression tree node

struct et

{

    char value;

    et* left, *right;

};

// A utility function to check if 'c'

// is an operator

bool isOperator(char c)

{

    if (c == '+' || c == '-' ||

            c == '*' || c == '/' ||

            c == '^')

        return true;

    return false;

}

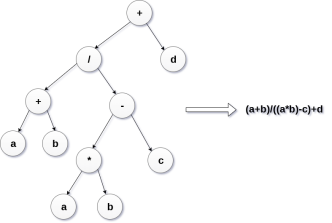
// Utility function to do inorder traversal

void inorder(et *t)

{

    if(t)

    {

        inorder(t->left);

        printf("%c ", t->value);

        inorder(t->right);

    }

}

// A utility function to create a new node

et* newNode(char v)

{

    et *temp = new et;

    temp->left = temp->right = NULL;

    temp->value = v;

    return temp;

};

// Returns root of constructed tree for given

// postfix expression

et* constructTree(char postfix[])

{

    stack<et *> st;

    et *t, *t1, *t2;

    // Traverse through every character of

    // input expression

    for (int i=0; i<strlen(postfix); i++)

    {

        // If operand, simply push into stack

        if (!isOperator(postfix[i]))

        {

            t = newNode(postfix[i]);

            st.push(t);

        }

        else // operator

        {

            t = newNode(postfix[i]);

            // Pop two top nodes

            t1 = st.top(); // Store top

            st.pop();      // Remove top

            t2 = st.top();

            st.pop();

            //  make them children

            t->right = t1;

            t->left = t2;

            // Add this subexpression to stack

            st.push(t);

        }

    }

    //  only element will be root of expression

    // tree

    t = st.top();

    st.pop();

    return t;

}

 // Driver program to test above

int main()

{

    char postfix[] = "ab+ef*g*-";

    et* r = constructTree(postfix);

    printf("infix expression is \n");

    inorder(r);

    return 0;

}

BFS

DFS

BFS finds the shortest path to the destination.

DFS goes to the bottom of a subtree, then backtracks.

The full form of BFS is Breadth-First Search.

The full form of DFS is Depth First Search.

It uses a queue to keep track of the next location to visit.

It uses a stack to keep track of the next location to visit.

BFS traverses according to tree level.

DFS traverses according to tree depth.

It is implemented using FIFO list.

It is implemented using LIFO list.

It requires more memory as compare to DFS.

It requires less memory as compare to BFS.

This algorithm gives the shallowest path solution.

This algorithm doesn't guarantee the shallowest path solution.

There is no need of backtracking in BFS.

There is a need of backtracking in DFS.

You can never be trapped into finite loops.

You can be trapped into infinite loops.

If you do not find any goal, you may need to expand many nodes before the solution is found.

If you do not find any goal, the leaf node backtracking may occur.

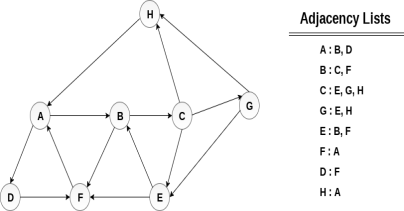
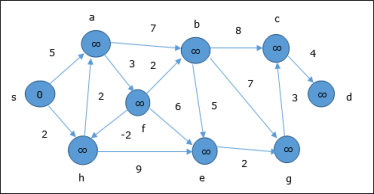
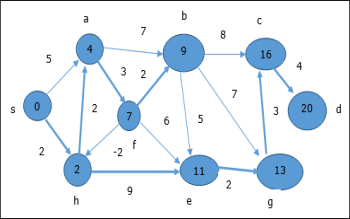
In the first step, all the vertices which are reachable from the source are updated by minimum cost. Hence, vertices a and h are updated.

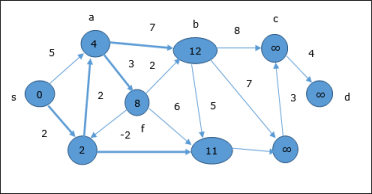
In the next step, vertices a, b, f and e are updated.

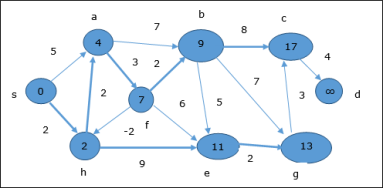
Following the same logic, in this step vertices b, f, c and g are updated.

Here, vertices c and d are updated.