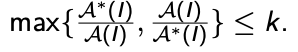Design & Analysis of Algorithms
Uinit-5Tractable and Intractable Problems Q1) What do you mean by NP complete ?A1) : NP Complete ● NP complete class is used to solve the problems of no polynomial time algorithm.● If a polynomial time algorithm exists for any of these problems, all problems in NP would be polynomial time solvable. These problems are called NP-complete.● The phenomenon of NP-completeness is important for both theoretical and practical reasons.● Following are the no polynomial run time algorithm: Hamiltonian cycles Optimal graph coloring Travelling salesman problem Finding the longest path in graph, etc Q2) Write the application of NP complete class ?A2) : NP Complete ClassClique ● A clique is a complete sub graph which is made by given undirected graph.● All the vertices are connected to each other i.e.one vertex of undirected graph is connected to all other vertices in graph.● There is the computational problem in clique where we can find the maximum clique of graph this known as max clique.● Max clique is used in many real world problems and in many application.● Assume a social networking where peoples are the vertices and they all are connected to each other via mutual acquaintance that becomes edges in graph.● In the above example clique represents a subset of people who know each other.● We can find max clique by taking one system which inspect all subsets.● But the brute force search is too time consuming for a network which has more than a few dozen vertices present in the graph.Example: ● Let's take an example where 1, 2, 3, 4, 5, 6 are the vertices that are connected to each other in an undirected graph.● Here subgraph contains 2,3,4,6 vertices which form a complete graph.● Therefore subgraph is a clique.● As this is a complete subgraph of a given graph. So it’s a 4-clique.
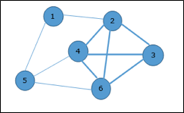
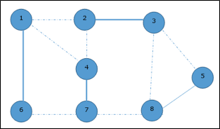
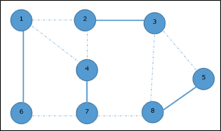
Analysis of Clique Algorithm● Non-deterministic algorithms use max clique algorithms to solve problems.● In this algorithm we first find all the vertices in the given graph.● Then we check if the graph is complete or not i.e. all vertices should form a complete graph.● The no polynomial time deterministic algorithm is used to solve this problem which is known as NP complete. 2. Vertex Cover● A vertex-cover of an undirected graph G = (V, E) is a subset of vertices V' ⊆ V such that if edge (u, v) is an edge of G, then either u in V or v in V' or both.● In a given undirected graph we need to find the maximum size of vertex cover.● It is the optimization version of NP complete problems.● It is easy to find vertex cover.Example:Given graph with set of edges are {(1,6),(1,2),(1,4),(2,3),(2,4),(6,7),(4,7),(7,8),(3,8),(3,5),(8,5)}
Now, start by selecting an edge (1, 6). Eliminate all the edges, which are either incident to vertex 1 or 6 and we add edge (1, 6) to cover.
In the next step, we have chosen another edge (2, 3) at random
Now we select another edge (4, 7).
We select another edge (8, 5).
Hence, the vertex cover of this graph is {1, 2, 4, 5}. Analysis of Vertex Cover Algorithm● In this algorithm, by using an adjacency list to represent E it is easy to see the running time of this algorithm is O (V+E). Q3) Write short notes on p class ?A3) : P Classes● The P class solves the problem of deterministic computation.● P class is used to solve the problems that are solvable in polynomial run time.● The problem belongs to class P if it’s easy to find a solution for the problem.● This problem can be solved by the worst case in O(nK) where k is constant.● The problems which are solved by P class are known as tractable problems and others are known as intractable or superpolynomial.● If polynomial time is P(n) then the algorithm can solve in time O (P(n)) with input size n.● The advantage of the class of polynomial time algorithms is that all reasonable deterministic single processor models of computation can be simulated on each other with at most polynomial slow-d. Q4) What are the np classes ?A4) : NP Classes ● The NP class solves the problem of non-deterministic computation.● The problem belongs to NP, if it’s easy to check a solution that may have been very tedious to find.● It solves the problem which is verifiable by polynomial time.● It is a class of decision problems.● For using this class, it is easy to check the correctness of the claimed answer even if it has extra information added in it.● Hence it is used to verify the solution is correct, not for finding the solution.● If there is a problem in this class then it can be solved by exhaustive search in exponential time. Q5) Write about np hard ?A5) : NP Hard ● A problem is in the class NPC if it is in NP and is as hard as any problem in NP.● A problem is NP-hard if all problems in NP are polynomial time reducible to it, even though it may not be in NP itself.● The problem in NP-Hard cannot be solved in polynomial time, until P = NP. ● If a problem is proved to be NPC, there is no need to waste time on trying to find an efficient algorithm for it. ● Instead, we can focus on design approximation algorithms.● Following are the NP hard class problems: Circuit satisfiability problem Set cover Vertex cover Travelling salesman problem Q6) Explain np complete problem ?A6) : NP Complete ProblemSteps for proving a problems as NP-completeFirst, try to prove it to be NP-hard, by :- Finding a related problem which is already found to be NP-hard (choosing such a suitable "source" problem close to your "target" problem, for the purpose of developing poly-trans, is the most difficult step), and then 2. Developing a truth-preserving polynomial problem-transformation from that source problem to your target problem. Significance : if anyone finds a poly algorithm for your “target” problem, then by using your poly-trans algorithm one would be able to solve that “source” NP-hard problem in poly-time, or in other words P would be = NP.Second, try to prove that the given problem is in NP-class: by developing a polynomial algorithm for checking any "certificate" of any problem-instance.The class P is the set of decision problems that can be solved in polynomial time. P = {L | L ⊆ {0, 1}* and there exists an algorithm A that decides L in polynomial time}. Q7) Describe approximation algorithm ?A7) : Approximation Algorithm An Approximate Algorithm is a way of approaching the optimization problem of NP-COMPLETENESS. This approach does not guarantee the right solution. The purpose of an approximation algorithm is to get as close as possible in a reasonable amount of time to the optimum value, which is at the most polynomial moment. These algorithms are called approximation algorithms or heuristic algorithms. ● The optimization issue is to find the shortest cycle for the travelling salesperson problem, and the approximation issue is to find a short cycle.● The optimization problem for the vertex cover problem is finding the vertex cover with the fewest vertices, and the approximation problem is finding the vertex cover with the fewest vertices. An algorithm A is said to be an algorithm, given an optimization problem P.Approximation algorithm for P if it returns an approximation algorithm for any given instance I, approximate solution, that is a feasible solution. Types of ApproximationP An optimization problem A An approximation algorithm I An instance of P A∗ (I) Optimal value for the instance I A(I) Value for the instance I generated by A Absolute Approximation ● A is an absolute approximation algorithm if a constant k exists. Such that I, of P, for every case, |A∗ (I) − A(I)| ≤ k.● Planar graph colouring, for instance. 2. Relative Approximation
Example :1. Vertex Cover 2. Traveling Salesman Problem 3. Bin Packing Q8) What is a randomized algorithm ?A8) : Randomized AlgorithmRandomized Algorithms use random numbers in order to decide what should be the next step to be performed. An example of the random algorithm can be like suppose there is a group of students in class and a professor is randomly making a student stand to answer the question. Randomized algorithms sometimes have deterministic time complexity. Algorithms like Monte Carlo algorithm use a randomized approach and its worst case complexity can be easily identified, whereas randomized algorithms like Las Vegas are dependent on the value of random variables and hence in these algorithms worst case identification becomes tougher.In order to compute expected time taken in the worst case an time taken by every possible value needs to be evaluated. Average of all evaluated times is the expected worst case time complexityRandomized algorithms are mainly used either to reduce the time complexity or the space complexity in the given algorithm. Q9) Define las vegas randomized algorithm ?A9) : Las Vegas Algorithm Las Vegas: - Lag Vegas algorithms usually produce correct or optimum results, here the time complexity is based on the random value and is evaluated as the expected value. An example of the Las Vegas algorithm is Randomized Quick sort in which the expected worst case time complexity is O(nlogn). Las Vegas algorithm is a randomized algorithm that always gives the correct result but gambles with resources.Example of Las VegasFinding Random point in the circleIt is easy and convenient to find a random point in the circle using these approach, here the idea is to first generate a point(x, y) with -1< x <1 and -1<y <1. So if the random selected point appear in this unit circle we keep it else we will throw it and repeat until the point in the unit circle is found Algorithm for finding Random point in the circle
Q10) What do you mean by monte carlo randomized algorithm ?A10) : Monte Carlo Algorithm Monte Carlo: - These algorithms produce the correct or optimum result on the basis of probability. Monte Carlo algorithm has deterministic running time and it is generally easier to find out worst case time complexity. For example implementation of Karger’s algorithm produces a minimum cut with probability greater than or equal to (1/n2) where n is the number of vertices in Karger’s algorithm and it has the worst case time complexity as O(E).Monte Carlo simulations are a broad class of algorithms that use repeated random sampling to obtain numerical results; these are generally used to simulate the behavior of other systems.If a point(x, y) with -1< x <1 and -1<y <1 are placed randomly then the ratio of points that fall within the unit circle will be close to .Algorithm to find a random point in the given circle using Monte Carlo approach
|
|
|
|
|
|
● A is a relative approximation algorithm if there exists a constant k Such that I, of P, for every case, ● Vertex cover
|
funpoint()(x,y float64) { for { x=2* rand.Float64()-1 y=2* rand.Float64()-1 if x*x+y*y < 1 { Return } } }
|
const a = 99999 count := 0 for i := 0; i <a; i++ { x := 2*rand.Float64() - 1 y := 2*rand.Float64() - 1 if x*x+y*y < 1 { count++ } }
|
0 matching results found