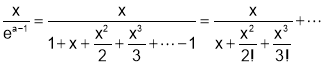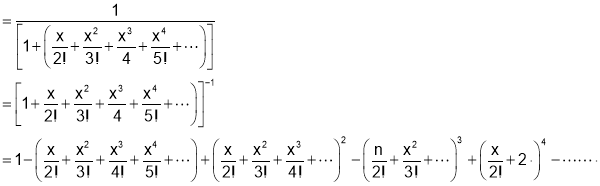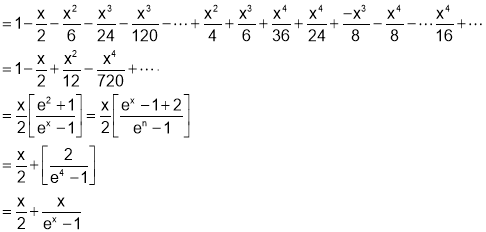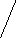Module 2
Limits, homogenous, Maxima Minima
Q1. If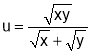 then verify Euler’s theorem for u.
then verify Euler’s theorem for u.
Sol 1. 
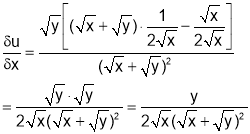
By symmetry,
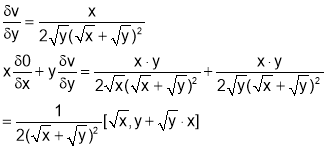

b) Put x=xt, y=yt we get
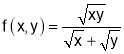
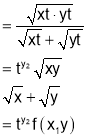
Thus u is homogenous function of 
Hence, by Euler’s Theorem
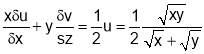
Q2. If 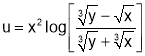 prove that
prove that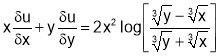
Sol 2. Putting x=xt, y=yt we get

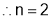
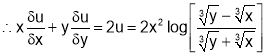
Q3. If 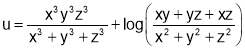 find value of
find value of 
Sol 3. Let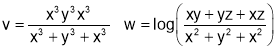
Let u=v+w
Putting x=xt, y=yt, z=zt
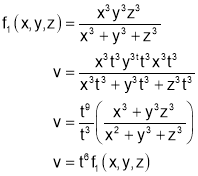
Thus v is homogenous function of degree 6.
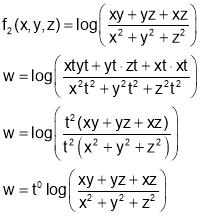
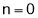
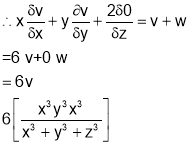
Q4. Find all stationary values of 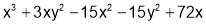
Sol 4: We have 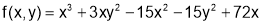
Step I: 
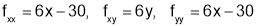
Step II: We now solve 
 i.e.
i.e. 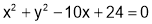
And 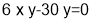
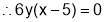
 or
or 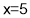
(i) When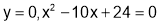

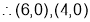 are stationary points.
are stationary points.
(ii) When 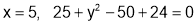
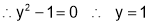 or
or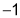 .
.
 and
and are stationary points.
are stationary points.
Step III: (i) When 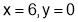
 and
and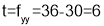
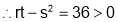 and
and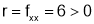
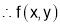 is minimum at
is minimum at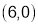 .
.
The minimum value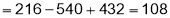 .
.
(ii) When 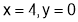
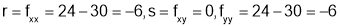
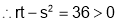 and
and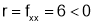
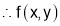 is maximum at
is maximum at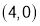 .
.
The maximum value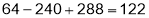
(iii) When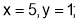

 is neither maximum nor minimum.
is neither maximum nor minimum.
(iv) When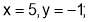
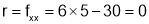
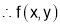 is neither maximum nor minimum
is neither maximum nor minimum
Q5. Find the minimum distance from the point 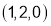 to the cone
to the cone 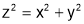
Sol 5: If 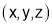 is any point on the cone, its distance from the point
is any point on the cone, its distance from the point 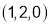 is
is
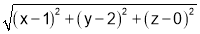
When the distance is minimum, its square is also minimum.
Step I : We have to find the stationary value of
 ………………(1)
………………(1)
With the condition that 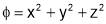 ………………….(2)
………………….(2)
Consider the Lagrange’s function
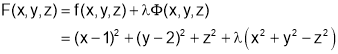
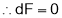 gives
gives
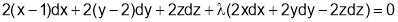
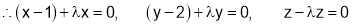 ………………….(3)
………………….(3)
Step II : We have to eliminate x, y, z from (1), (2) and (3).
From (3),
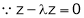
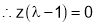
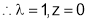
Hence, 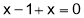
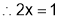
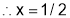

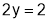

Hence, the required point is 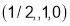 .
.
The distance between 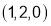 and
and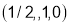 is
is
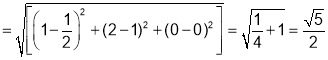
Q6. If 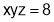 , find the values of x, y, z for which
, find the values of x, y, z for which 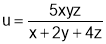 is maximum.
is maximum.
Sol6 : We have to maximize 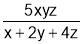 with the condition that
with the condition that 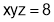 .
.
This means we have to maximize 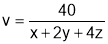
i.e. we have to minimize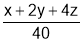 i.e.
i.e. 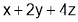
Step I : We have to minimize 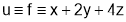 ………………(1)
………………(1)
With the condition that 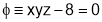 ……………….(2)
……………….(2)
Consider the Lagrange’s function,
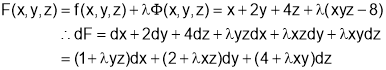
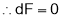 gives
gives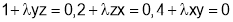
But 
and
Q7. Prove that 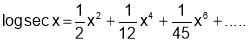
SOL7: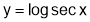

Diff wrt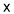
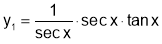
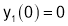
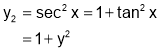
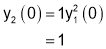
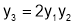
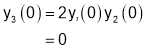
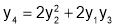

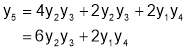
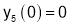
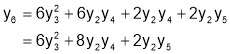
Hence by Maclaurin’s Series
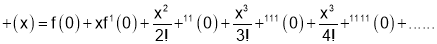 we get
we get
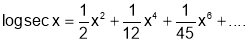
Q8. Expand 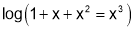 upto
upto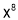
Sol 8:We have 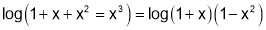
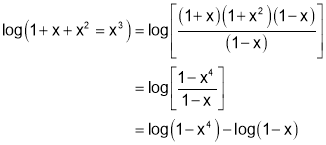

Q9. Prove that 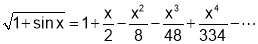
Sol 9. We have
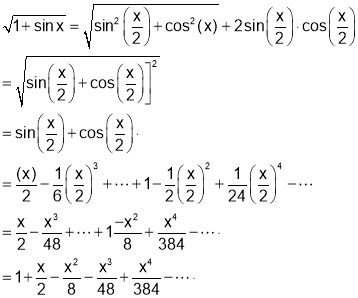
Q10. Expand in Power of 
Hence Prove that 
Sol 10.