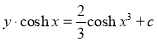Module 4
First Order Ordinary Differential Equations
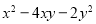

Solution
We have 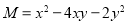 and
and 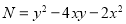
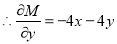 and
and 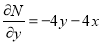
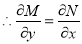
Hence, the given equation is exact.
Now, 
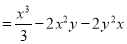
And 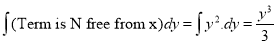
 The Solution is
The Solution is 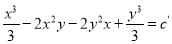
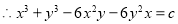
2. Solve 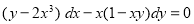
Solution:
We have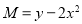 and
and 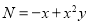
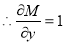 and
and 

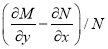 =
=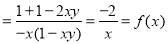
 I.F.
I.F. 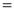
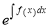
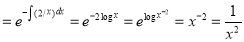
Multiplying by 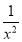 we get
we get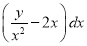
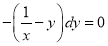 , which is exact.
, which is exact.

And 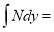
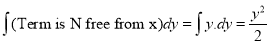
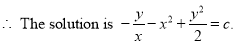
3. Solve 
Solution:
We have  and
and 
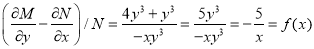
 I.F
I.F 
Multiplying the given equation by , we get
, we get 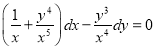
which is exact

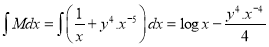
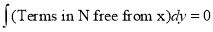
 The solution is
The solution is 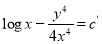

4. Solve 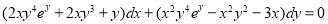
Solution:
We have, 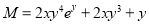
and 
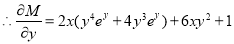
And 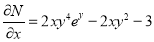

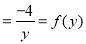
 I.F
I.F 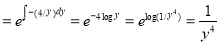
Multiplying the given equation by I.F, we get
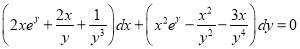 which is exact
which is exact
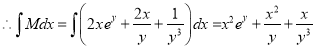

 The solution is
The solution is 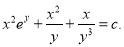
5. Solve 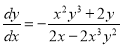
Solution:
The equation can be written as
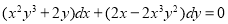
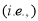
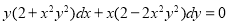
The equation is of the above form and
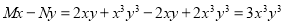
Dividing the equation by 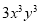 , we get
, we get
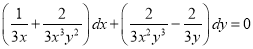
Now, 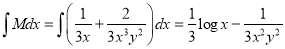
And 
 The solution is
The solution is 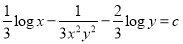
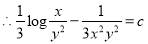
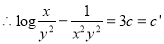
6. Solve 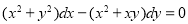
Solution:
The equation is homogeneous and
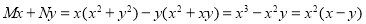
Hence, 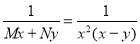 is an integrating factor.
is an integrating factor.
Dividing by 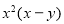 , we get
, we get 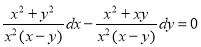
Now this is an exact differential equation.
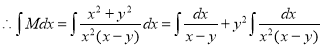
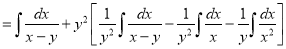
(By partial fraction treating y constant. Let 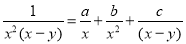 )
)
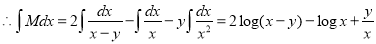
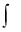 (Terms in N free from x)
(Terms in N free from x) 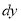
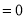
 The solution is
The solution is 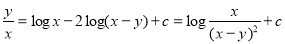
7. Solve 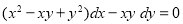
Solution:
The equation is homogeneous and
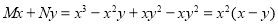
Hence,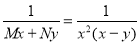 is an integrating factor.
is an integrating factor.
Dividing by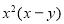 we get
we get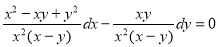
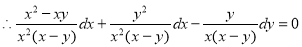

By partial fraction as in(A) of Ex.3 above)
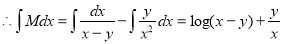
 (Terms in N free from x)
(Terms in N free from x) 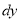
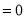
 The solution is
The solution is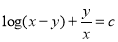
8. Solve 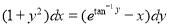
Solution:
Equation can be written as
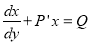

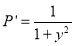 and
and 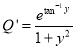
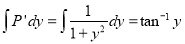
Solution is
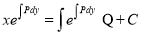
To solve put 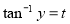
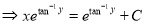
9. Solve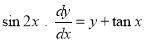
Solution:
The equation can be written as 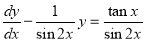 , which is linear.
, which is linear.
Now, 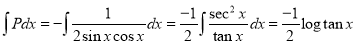
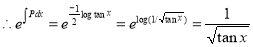
 The solution is
The solution is 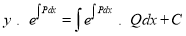
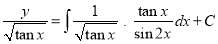
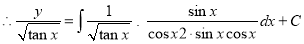
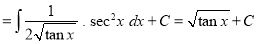
 The solution is
The solution is 
10. Solve 
Solution:
We have 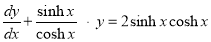
This is linear of the form 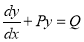
I.F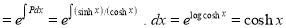
 The solution is
The solution is 
Put 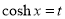

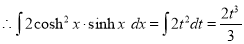
 The solution is
The solution is