Unit - 2
Problem-solving
Q1) What do you mean by solving problems by searching?
A1) In Artificial Intelligence, search techniques are universal problem-solving procedures. To solve a given problem and deliver the optimum outcome, rational agents or problem-solving agents in AI used these search techniques or algorithms. Problem-solving agents are goal-based agents that use atomic representation. In this subject, we will explore a variety of problem-solving search approaches.
Searching Algorithms Terminologies:
- Search: In a given search space, searching is a step-by-step procedure for addressing a search problem. There are three primary variables that can influence the outcome of a search:
- Search space: A search space is a collection of probable solutions that a system could have.
- Start state: It's the starting point for the agent's quest.
- Goal test: It's a function that looks at the current state and returns whether or not the goal state has been reached.
- Search tree: Search tree is a tree representation of a search problem. The root node, which corresponds to the initial state, is at the top of the search tree.
- Actions: It provides the agent with a list of all available actions.
- Transition model: A transition model is a description of what each action does.
- Path cost: It's a function that gives each path a numerical cost.
- Solutions: It is an action sequence that connects the start and end nodes.
- Optimal solutions: If a solution is the cheapest of all the options.
Formulating problems
The problem of getting to Bucharest had been previously defined in terms of the starting state, activities, transition model, goal test, and path cost. Despite the fact that this formulation appears to be reasonable, it is still a model—an abstract mathematical description—rather than the real thing.
Compare our simple state description, In (Arad), to a cross-country trip, where the state of the world includes a wide range of factors such as the traveling companions, what's on the radio, the scenery out the window, whether there are any law enforcement officers nearby, how far it is to the next rest stop, the road condition, the weather, and so on.
All of these factors aren't mentioned in our state descriptions because they have nothing to do with finding a route to Bucharest. The process of removing details from a representation is known as abstraction.
In addition to the state description, we must abstract both the state description and the actions themselves. A driving action can result in a number of different outcomes. It takes time, consumes fuel, emits emissions, and changes the agent, in addition to shifting the vehicle's and its occupants' positions (as they say, travel is broadening). In our system, only the change in position is taken into account.
Can we be more precise about the proper level of abstraction? Consider the abstract states and actions we've selected as large collections of detailed world states and action sequences. Consider a path from Arad to Sibiu to Rimnicu Vilcea to Pitesti to Bucharest as an example of a solution to the abstract problem. A wide number of more detailed paths correlate to this abstract solution.
Searching for solution
We must now address the issues we've identified. Because a solution consists of a series of activities, search algorithms consider a number of different action sequences. The SEARCH TREE possible action sequences start with the starting state and build a search tree with the initial state NODE at the root; the branches are actions, and the nodes are states in the problem's state space.
Figure depicts the first few steps in developing a search tree for finding a route from Arad to Bucharest. The root node of the tree represents the initial state (Arad). The first stage is to determine whether or not this is a goal state. (Of course, it isn't, but it's worth double-checking to avoid problems like "starting in Arad, get to Arad.") Then we must weigh a number of possibilities. This is done by extending the current state; in other words, each legal action is applied to the existing state, resulting in the production of a new set of states. In this scenario, we create three additional child nodes from the parent node In(Arad): In(Sibiu), In(Timisoara), and In(Sibiu) (Zerind).
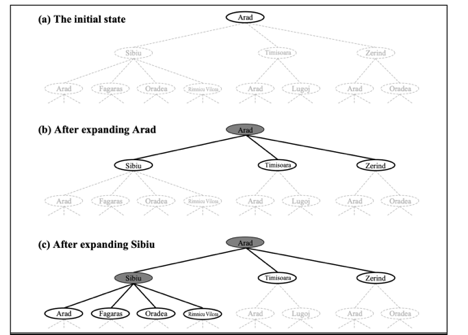
Fig 1: Partial search tree
This is the essence of searching: pursuing one option at a time while putting the others on hold in the event that the first does not yield a solution. Let's use Sibiu as an example. We first check to see whether it's a target state (it isn't), then expand it to get In(Arad), In(Fagaras), In(Oradea), and In(Oradea) (RimnicuVilcea). Then we can choose one of these four possibilities, or we can go back to LEAF NODE and choose Timisoara or Zerind. Each of these six nodes in the tree is a leaf node, which means it has no progeny.
At any given FRONTIER point, the frontier is the collection of all leaf nodes that are available for expansion. Each tree's border is defined by the nodes with bold outlines in Figure.
The process of choosing and expanding nodes on the frontier continues until a solution is found or no more states can be added to the frontier. Informally, the TREE-SEARCH algorithm is depicted in the figure. All search algorithms have the same core basis; the difference is in how they choose which state to expand next—the so-called search strategy.
Function TREE-SEARCH (problem) returns a solution, or failure
Initialize the frontier using the initial state of problem
Loop do
If the frontier is empty then return failure
Choose a leaf node and remove it from the frontier
If the node contains a goal state then return the corresponding solution
Expand the chosen node, adding the resulting nodes to the frontier
Function GRAPH-SEARCH(problem) returns a solution, or failure
Initialize the explored set to be empty
Loop do
If the frontier is empty then return failure
Choose a leaf node and remove it from the frontier
If the node contains a goal state then return the corresponding solution
Add the node to the explored set
Expand the chosen node, adding the resulting nodes to frontier
Only if not in the frontier or explored set
Q2) What are Problem solving agents?
A2) By defining problems and their various solutions, the problem-solving agent performs exactly.
In the field of Artificial Intelligence, a problem-solving agent is a goal-based agent that focuses on goals. It is one embodiment of a combination of algorithms and strategies to tackle a well-defined problem. These agents differ from reflex agents in that they only have to map states into actions and are unable to map when storing and learning are both larger. The following are the stages that problem-solving agents go through to reach a desired state or solution:
● Articulating or expressing the desired goal and the problem is tried upon, clearly.
● Explore and examine
● Find the solution from the various algorithms on the table.
● The final step is Execution!
The steps taken by the problem-solving agent
● Goal formulation: is the first and most basic step in solving a problem. It organises the steps/sequence needed to construct a single goal from many goals, as well as the actions needed to achieve that goal. The existing circumstance and the agent's performance measure are used to formulate goals.
● Problem formulation: is the most crucial step in the problem-solving process because it determines what activities should be taken to attain the stated goal. In the formulation of a problem, there are five elements to consider:
● First State: This is the agent's initial state, or first step toward its goal.
● Actions: This is a list of the several options available to the agent.
● Transition Model: The Transition Model explains what each step does.
● Goal test: It determines whether or not a given state is a desired state.
● Path cost: Each path that leads to the goal is given a numerical cost. A cost function is chosen by the problem-solving agent to reflect its performance measure. Remember that the optimal option has the cheapest path cost of all the alternatives.
Note that the problem's state-space is implicitly defined by the initial state, actions, and transition model. A problem's state-space is a collection of all states that can be achieved by following any series of activities from the beginning state. The state-space is represented as a directed map or graph, with nodes representing states, links between nodes representing actions, and a path representing a series of states connected by a series of actions.
● Search - It determines the best potential sequence of actions to get from the current condition to the goal state. It receives an issue as input and returns a solution as output.
● Solution - It selects the best algorithm from a set of algorithms that can be demonstrated to be the most optimal solution.
● Execution - It uses the best optimal solution found by the searching algorithms to get from the present state to the goal state.
Q3) Write any example of problems?
A3) In general, there are two sorts of problem-solving strategies:
● Toy problem - Researchers use it to compare the performance of algorithms because it provides a succinct and clear explanation of the problem.
● Real world problem - The problems that need to be solved are those that occur in the real world. It does not require descriptions, unlike a toy problem, yet we can have a generic formulation of the problem.
- Some Toy Problems
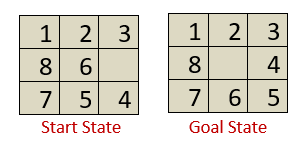
8 Puzzle Problem: A 33 matrix with moveable tiles numbered 1 to 8 and a vacant area is shown. The tile to the left of the vacant spot can be slid into it. The goal is to achieve a goal state that is similar to the one indicated in the diagram below.
Our goal is to slide digits into the blank space in the figure to change the current state to the goal state.
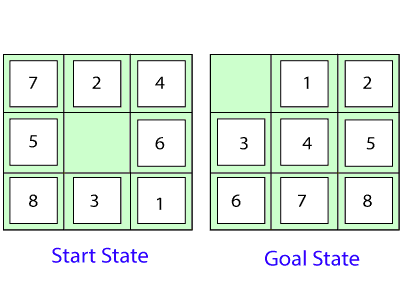
Fig 2: 8 puzzle problem
By sliding digits into the vacant space in the above diagram, we can change the current (Start) state to the desired state.
The following is the problem statement:
● States: It shows where each numbered tile and the blank tile are located.
● Initial State: Any state can be used as the starting point.
● Actions: The blank space's actions are defined here, i.e., left, right, up, or down.
● Transition model: It returns the final state, which is determined by the provided state and actions.
● Goal test: It determines if we have arrived at the correct goal-state.
● Path cost: The path cost is the number of steps in a path where each step costs one dollar.
8-queens problem: The goal of this issue is to arrange eight queens on a chessboard in such a way that none of them can attack another queen. A queen can attack other queens in the same row and column or diagonally.
We can grasp the problem and its correct solution by looking at the diagram below.

Fig 3: 8 queen puzzle
As can be seen in the diagram above, each queen is put on the chessboard in such a way that no other queen is placed diagonally, in the same row or column. As a result, it is one viable solution to the eight-queens dilemma.
For this problem, there are two main kinds of formulation:
Incremental formulation: It begins with an empty state and progresses in steps, with the operator augmenting a queen at each step.
Following steps are involved in this formulation:
● States: Arrangement of any 0 to 8 queens on the chessboard.
● Initial State: An empty chessboard
● Actions: Add a queen to any empty box.
● Transition model: Returns the chessboard with the queen added in a box.
● Goal test: Checks whether 8-queens are placed on the chessboard without any attack.
● Path cost: There is no need for path cost because only final states are counted.
In this formulation, there is approximately 1.8 x 1014 possible sequence to investigate.
Complete-state formulation: It starts with all the 8-queens on the chessboard and moves them around, saving from the attacks.
In this formulation, the steps are as follows:
States: Each of the eight queens is arranged in a column, with no queen assaulting the other.
Actions: Move the queen to a spot where it will be secure from attacks.
This formulation is superior to the incremental formulation since it shrinks the state space from 1.8 x 1014 to 2057 and makes finding solutions much easier.
2. Some Real-world problems
Traveling salesperson problem(TSP): It's a problem of touring, because the salesman can only visit each city once. The goal is to discover the shortest tour and sell out all of the merchandise in each place.
VLSI Layout problem: Millions of components and connections are placed on a chip in order to reduce area, circuit delays, and stray capacitances while increasing manufacturing yield.
The layout problem is split into two parts:
● Cell layout: The circuit's primitive components are arranged into cells, each of which performs a distinct purpose. Each cell is the same size and shape. The goal is to arrange the cells on the chip so that they do not overlap.
● Channel routing: It determines a unique path through the spaces between the cells for each wire.
● Protein Design: The goal is to develop an amino acid sequence that will fold into a 3D protein with the ability to treat an illness.
Q4) Write about search algorithms?
A4) Problem-solving agents:
In Artificial Intelligence, Search techniques are universal problem-solving methods. Rational agents or Problem-solving agents in AI mostly used these search strategies or algorithms to solve a specific problem and provide the best result. Problem-solving agents are the goal-based agents and use atomic representation.
Search Algorithm Terminologies:
● Search: Searching Is a step by step procedure to solve a search-problem in a given search space. A search problem can have three main factors:
- Search Space: Search space represents a set of possible solutions, which a system may have.
- Start State: It is a state from where agent begins the search.
- Goal test: It is a function which observe the current state and returns whether the goal state is achieved or not.
● Search tree: A tree representation of search problem is called Search tree. The root of the search tree is the root node which is corresponding to the initial state.
● Actions: It gives the description of all the available actions to the agent.
● Transition model: A description of what each action do, can be represented as a transition model.
● Path Cost: It is a function which assigns a numeric cost to each path.
● Solution: It is an action sequence which leads from the start node to the goal node.
● Optimal Solution: If a solution has the lowest cost among all solutions.
Properties of Search Algorithms:
Following are the four essential properties of search algorithms to compare the efficiency of these algorithms:
Completeness: A search algorithm is said to be complete if it guarantees to return a solution if at least any solution exists for any random input.
Optimality: If a solution found for an algorithm is guaranteed to be the best solution (lowest path cost) among all other solutions, then such a solution for is said to be an optimal solution.
Time Complexity: Time complexity is a measure of time for an algorithm to complete its task.
Space Complexity: It is the maximum storage space required at any point during the search, as the complexity of the problem.
Types of search algorithms
Based on the search problems we can classify the search algorithms into uninformed (Blind search) search and informed search (Heuristic search) algorithms.
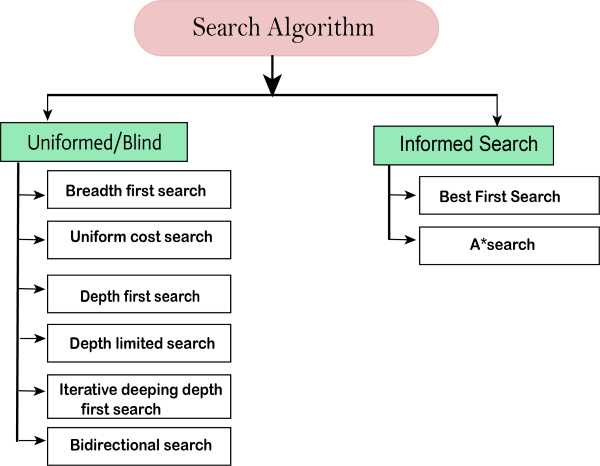
Fig 4: Search algorithm
Uninformed/Blind Search:
The uninformed search does not contain any domain knowledge such as closeness, the location of the goal. It operates in a brute-force way as it only includes information about how to traverse the tree and how to identify leaf and goal nodes. Uninformed search applies a way in which search tree is searched without any information about the search space like initial state operators and test for the goal, so it is also called blind search. It examines each node of the tree until it achieves the goal node.
It can be divided into five main types:
● Breadth-first search
● Uniform cost search
● Depth-first search
● Iterative deepening depth-first search
● Bidirectional Search
Informed Search
Informed search algorithms use domain knowledge. In an informed search, problem information is available which can guide the search. Informed search strategies can find a solution more efficiently than an uninformed search strategy. Informed search is also called a Heuristic search.
A heuristic is a way which might not always be guaranteed for best solutions but guaranteed to find a good solution in reasonable time.
Informed search can solve much complex problem which could not be solved in another way.
An example of informed search algorithms is a traveling salesman problem.
- Greedy Search
- A* Search
Q5) Describe breadth first search?
A5) Breadth-first Search:
● Breadth-first search is the most common search strategy for traversing a tree or graph. This algorithm searches breadthwise in a tree or graph, so it is called breadth-first search.
● BFS algorithm starts searching from the root node of the tree and expands all successor node at the current level before moving to nodes of next level.
● The breadth-first search algorithm is an example of a general-graph search algorithm.
● Breadth-first search implemented using FIFO queue data structure.
Advantages:
● BFS will provide a solution if any solution exists.
● If there are more than one solutions for a given problem, then BFS will provide the minimal solution which requires the least number of steps.
Disadvantages:
● It requires lots of memory since each level of the tree must be saved into memory to expand the next level.
● BFS needs lots of time if the solution is far away from the root node.
Example:
In the below tree structure, we have shown the traversing of the tree using BFS algorithm from the root node S to goal node K. BFS search algorithm traverse in layers, so it will follow the path which is shown by the dotted arrow, and the traversed path will be:
S---> A--->B---->C--->D---->G--->H--->E---->F---->I---->K
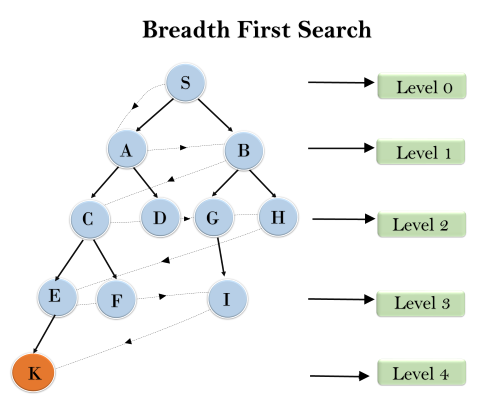
Time Complexity: Time Complexity of BFS algorithm can be obtained by the number of nodes traversed in BFS until the shallowest Node. Where the d= depth of shallowest solution and b is a node at every state.
T (b) = 1+b2+b3+.......+ bd= O (bd)
Space Complexity: Space complexity of BFS algorithm is given by the Memory size of frontier which is O(bd).
Completeness: BFS is complete, which means if the shallowest goal node is at some finite depth, then BFS will find a solution.
Optimality: BFS is optimal if path cost is a non-decreasing function of the depth of the node.
Q6) Explain depth first search?
A6) Depth-first Search
● Depth-first search isa recursive algorithm for traversing a tree or graph data structure.
● It is called the depth-first search because it starts from the root node and follows each path to its greatest depth node before moving to the next path.
● DFS uses a stack data structure for its implementation.
● The process of the DFS algorithm is similar to the BFS algorithm.
Note: Backtracking is an algorithm technique for finding all possible solutions using recursion.
Advantage:
● DFS requires very less memory as it only needs to store a stack of the nodes on the path from root node to the current node.
● It takes less time to reach to the goal node than BFS algorithm (if it traverses in the right path).
Disadvantage:
● There is the possibility that many states keep re-occurring, and there is no guarantee of finding the solution.
● DFS algorithm goes for deep down searching and sometime it may go to the infinite loop.
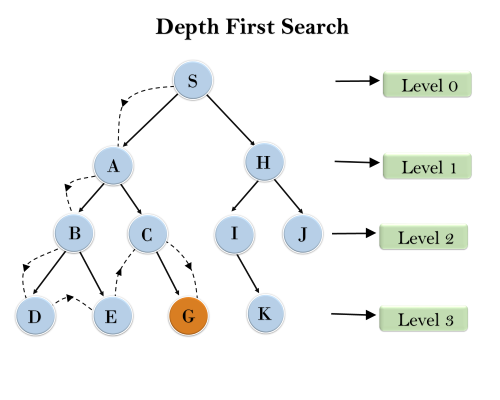
Example:
In the below search tree, we have shown the flow of depth-first search, and it will follow the order as:
Root node--->Left node ----> right node.
It will start searching from root node S, and traverse A, then B, then D and E, after traversing E, it will backtrack the tree as E has no other successor and still goal node is not found. After backtracking it will traverse node C and then G, and here it will terminate as it found goal node.
Completeness: DFS search algorithm is complete within finite state space as it will expand every node within a limited search tree.
Time Complexity: Time complexity of DFS will be equivalent to the node traversed by the algorithm. It is given by:
T(n)= 1+ n2+ n3 +.........+ nm=O(nm)
Where, m= maximum depth of any node and this can be much larger than d (Shallowest solution depth)
Space Complexity: DFS algorithm needs to store only single path from the root node, hence space complexity of DFS is equivalent to the size of the fringe set, which is O(bm).
Optimal: DFS search algorithm is non-optimal, as it may generate a large number of steps or high cost to reach to the goal node.
Q7) What is depth limited search algorithm?
A7) Depth-Limited Search Algorithm:
A depth-limited search algorithm is similar to depth-first search with a predetermined limit. Depth-limited search can solve the drawback of the infinite path in the Depth-first search. In this algorithm, the node at the depth limit will treat as it has no successor nodes further.
Depth-limited search can be terminated with two Conditions of failure:
● Standard failure value: It indicates that problem does not have any solution.
● Cutoff failure value: It defines no solution for the problem within a given depth limit.
Advantages:
Depth-limited search is Memory efficient.
Disadvantages:
● Depth-limited search also has a disadvantage of incompleteness.
● It may not be optimal if the problem has more than one solution.
Example:
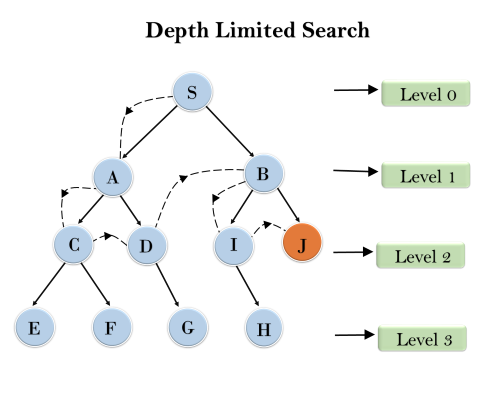
Completeness: DLS search algorithm is complete if the solution is above the depth-limit.
Time Complexity: Time complexity of DLS algorithm is O(bℓ).
Space Complexity: Space complexity of DLS algorithm is O(b×ℓ).
Optimal: Depth-limited search can be viewed as a special case of DFS, and it is also not optimal even if ℓ>d.
Q8) Define uniform cost search algorithm?
A8) Uniform-cost Search Algorithm:
Uniform-cost search is a searching algorithm used for traversing a weighted tree or graph. This algorithm comes into play when a different cost is available for each edge. The primary goal of the uniform-cost search is to find a path to the goal node which has the lowest cumulative cost. Uniform-cost search expands nodes according to their path costs form the root node. It can be used to solve any graph/tree where the optimal cost is in demand. A uniform-cost search algorithm is implemented by the priority queue. It gives maximum priority to the lowest cumulative cost. Uniform cost search is equivalent to BFS algorithm if the path cost of all edges is the same.
Advantages:
● Uniform cost search is optimal because at every state the path with the least cost is chosen.
Disadvantages:
● It does not care about the number of steps involve in searching and only concerned about path cost. Due to which this algorithm may be stuck in an infinite loop.
Example:
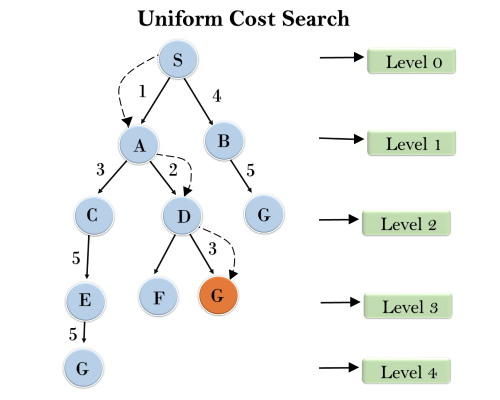
Completeness:
Uniform-cost search is complete, such as if there is a solution, UCS will find it.
Time Complexity:
Let C* is Cost of the optimal solution, and ε is each step to get closer to the goal node. Then the number of steps is = C*/ε+1. Here we have taken +1, as we start from state 0 and end to C*/ε.
Hence, the worst-case time complexity of Uniform-cost search isO(b1 + [C*/ε])/.
Space Complexity:
The same logic is for space complexity so, the worst-case space complexity of Uniform-cost search is O(b1 + [C*/ε]).
Optimal:
Uniform-cost search is always optimal as it only selects a path with the lowest path cost.
Q9) Explain iterative deepening depth first search?
A9) Iterative deepening depth-first Search:
The iterative deepening algorithm is a combination of DFS and BFS algorithms. This search algorithm finds out the best depth limit and does it by gradually increasing the limit until a goal is found.
This algorithm performs depth-first search up to a certain "depth limit", and it keeps increasing the depth limit after each iteration until the goal node is found.
This Search algorithm combines the benefits of Breadth-first search's fast search and depth-first search's memory efficiency.
The iterative search algorithm is useful uninformed search when search space is large, and depth of goal node is unknown.
Advantages:
● It Combines the benefits of BFS and DFS search algorithm in terms of fast search and memory efficiency.
Disadvantages:
● The main drawback of IDDFS is that it repeats all the work of the previous phase.
Example:
Following tree structure is showing the iterative deepening depth-first search. IDDFS algorithm performs various iterations until it does not find the goal node. The iteration performed by the algorithm is given as:
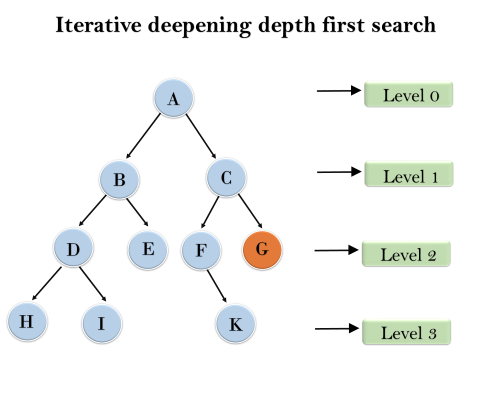
1'st Iteration-----> A
2'nd Iteration----> A, B, C
3'rd Iteration------>A, B, D, E, C, F, G
4'th Iteration------>A, B, D, H, I, E, C, F, K, G
In the fourth iteration, the algorithm will find the goal node.
Completeness:
This algorithm is complete is ifthe branching factor is finite.
Time Complexity:
Let's suppose b is the branching factor and depth is d then the worst-case time complexity is O(bd).
Space Complexity:
The space complexity of IDDFS will be O(bd).
Optimal:
IDDFS algorithm is optimal if path cost is a non- decreasing function of the depth of the node.
Q10) What is bidirectional search algorithm?
A10) Bidirectional Search Algorithm:
Bidirectional search algorithm runs two simultaneous searches, one form initial state called as forward-search and other from goal node called as backward-search, to find the goal node. Bidirectional search replaces one single search graph with two small subgraphs in which one starts the search from an initial vertex and other starts from goal vertex. The search stops when these two graphs intersect each other.
Bidirectional search can use search techniques such as BFS, DFS, DLS, etc.
Advantages:
● Bidirectional search is fast.
● Bidirectional search requires less memory
Disadvantages:
● Implementation of the bidirectional search tree is difficult.
● In bidirectional search, one should know the goal state in advance.
Example:
In the below search tree, bidirectional search algorithm is applied. This algorithm divides one graph/tree into two sub-graphs. It starts traversing from node 1 in the forward direction and starts from goal node 16 in the backward direction.
The algorithm terminates at node 9 where two searches meet.
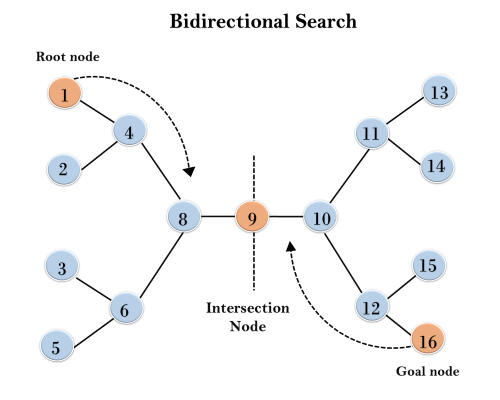
Completeness: Bidirectional Search is complete if we use BFS in both searches.
Time Complexity: Time complexity of bidirectional search using BFS is O(bd).
Space Complexity: Space complexity of bidirectional search is O(bd).
Optimal: Bidirectional search is Optimal.
Q11) Describe uninformed search strategies?
A11) Uninformed search, also known as blind, exhaustive, or brute-force search, is a type of search that doesn't use any information about the problem to guide it and so isn't very efficient.
Breadth first search
The breadth first search technique is a general strategy for traversing a graph. A breadth first search takes up more memory, but it always discovers the shortest path first. In this type of search, the state space is represented as a tree. The answer can be discovered by traveling the tree. The tree's nodes indicate the initial value of starting state, multiple intermediate states, and the end state.
This search makes use of a queue data structure, which is traversed level by level. In a breadth first search, nodes are extended in order of their distance from the root. It's a path-finding algorithm that, if one exists, can always find a solution. The answer that is discovered is always the alternative option. This task demands a significant amount of memory. At each level, each node in the search tree is increased in breadth.
Algorithm:
Step 1: Place the root node inside the queue.
Step 2: If the queue is empty then stops and returns failure.
Step 3: If the FRONT node of the queue is a goal node, then stop and return success. Step 4: Remove the FRONT node from the queue. Process it and find all its neighbours that are in a ready state then place them inside the queue in any order.
Step 5: Go to Step 3.
Step 6: Exit.
Implementations
Let us implement the above algorithm of BFS by taking the following suitable example
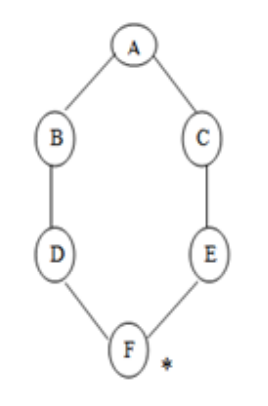
Fig 5: Example
Consider the graph below, where A is the initial node and F is the destination node (*).
Step 1: Place the root node inside the queue i.e. A
Step 2: The queue is no longer empty, and the FRONT node, i.e. A, is no longer our goal node. So, proceed to step three.
Step 3: Remove the FRONT node, A, from the queue and look for A's neighbors, B and C.
Step 4: Now, b is the queue's FRONT node. As a result, process B and look for B's neighbors, i.e., D.
Step 5: Find out who C's neighbors are, which is E.

Ste 6: As D is the queue's FRONT node, find out who D's neighbors are.
Step 7: E is now the queue's first node. As a result, E's neighbor is F, which is our objective node.
Step 8: Finally, F is the FRONT of the queue, which is our goal node. As a result, leave.
Advantages
● The goal will be achieved in whatever way possible using this strategy.
● It does not take any unproductive pathways for a long time.
● It finds the simplest answer in the situation of several pathways.
Disadvantages
● BFS consumes a significant amount of memory.
● It has a greater level of time complexity.
● It has long pathways when all paths to a destination have about the same search depth.
Q12) Explain informed search strategies?
A12) A heuristic is a technique for making our search process more efficient. Some heuristics assist in the direction of a search process without claiming completeness, whereas others do. A heuristic is a piece of problem-specific knowledge that helps you spend less time looking for answers. It's a strategy that works on occasion, but not all of the time.
The heuristic search algorithm uses the problem information to help steer the way over the search space. These searches make use of a number of functions that, assuming the function is efficient, estimate the cost of going from where you are now to where you want to go.
A heuristic function is a function that converts problem situation descriptions into numerical measures of desirability. The heuristic function's objective is to direct the search process in the most profitable routes by recommending which path to take first when there are multiple options.
The following procedures should be followed when using the heuristic technique to identify a solution:
1. Add domain—specific information to select what is the best path to continue searching along.
2. Define a heuristic function h(n) that estimates the ‘goodness’ of a node n. Specifically, h(n) = estimated cost (or distance) of minimal cost path from n to a goal state.
3. The term heuristic means ‘serving to aid discovery’ and is an estimate, based on domain specific information that is computable from the current state description of how close we are to a goal.
A search problem in which multiple search orders and the use of heuristic knowledge are clearly understood is finding a path from one city to another.
1. State: The current city in which the traveller is located.
2. Operators: Roads linking the current city to other cities.
3. Cost Metric: The cost of taking a given road between cities.
4. Heuristic information: The search could be guided by the direction of the goal city from the current city, or we could use airline distance as an estimate of the distance to the goal.
Q13) Define heuristic function?
A13) As we've seen, an informed search employs heuristic functions in order to get at the destination node in a more conspicuous manner. As a result, there are various ways to get from the present node to the goal node in a search tree. It is undeniably important to choose a decent heuristic function. The efficiency of a heuristic function determines its usefulness. The more knowledge about the problem there is, the longer it takes to solve it.
A heuristic function can help solve some toy problems more efficiently, such as 8-puzzle, 8-queen, tic-tac-toe, and so on. Let's have a look at how:
Consider the eight-puzzle issue below, which has a start and a target state. Our goal is to slide the tiles from the current/start state into the goal state in the correct order. There are four possible movements: left, right, up, and down. There are various ways to transform the current/start state to the desired state, but we can solve the problem more efficiently by using the heuristic function h(n).
The following is a heuristic function for the 8-puzzle problem:
h(n)=Number of tiles out of position.
So, there are three tiles that are out of place, namely 6, 5, and 4. The empty tile in the goal state is not counted). h(n)=3 in this case. The value of h(n) =0 must now be minimised.
To reduce the h(n) value to 0, we can build a state-space tree as shown below:
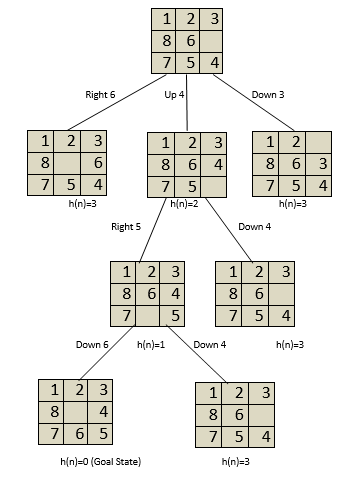
The objective state is minimised from h(n)=3 to h(n)=0, as seen in the state space tree above. However, depending on the requirement, we can design and employ a number of heuristic functions. A heuristic function h(n) can alternatively be defined as the knowledge needed to solve a problem more efficiently, as shown in the previous example. The information can be related to the nature of the state, the cost of changing states, the characteristics of target nodes, and so on, and is stated as a heuristic function.
Q14) What is search in complex environments?
A14) Agents rarely have complete control over their surroundings, and are more likely to have only partial control. This implies that they have control over the environment. Changes in the environment, in turn, will have a direct impact on the agents in the environment.
Environments are often described as non-deterministic. That is to say, activities taken in particular circumstances may fail. Furthermore, an agent executing the same task in two different contexts can provide radically different results.
An agent in an environment will have a pre-programmed set of talents that it may use to deal with various circumstances it may encounter. Effectoric capacities are the name given to these skills. The agent has a sensor that is plainly affected by the surroundings, as seen in the diagram on agents. The agent can use data from this sensor with previously collected data to determine which action to take.
Obviously, not every action can be carried out in every circumstance. An agent, for example, might be able to 'open door,' but only if the door is unlocked. A precondition is that the door must be unlocked before the action may be conducted.
The most difficult difficulty that agents face in an environment is determining which action to take at any given time in order to maximise their chances of achieving their goal, or at least working toward it. The qualities of an environment influence the complexity of a decision-making process.
There are several types of environments:
● Fully Observable vs Partially Observable
● Deterministic vs Stochastic
● Competitive vs Collaborative
● Single-agent vs Multi-agent
● Static vs Dynamic
● Discrete vs Continuous
Fully Observable vs Partially Observable
● A fully observable environment is one in which an agent sensor can perceive or access the complete state of an agent at any given time; otherwise, it is a partially observable environment.
● It's simple to preserve a completely observable environment because there's no need to keep track of the environment's past.
● When the agent has no sensors in all environments, it is said to be unobservable.
Deterministic vs Stochastic
● The environment is considered to be deterministic when a uniqueness in the agent's present state totally determines the agent's next state.
● The stochastic environment is random in nature, not unique, and the agent cannot entirely control it.
Competitive vs Collaborative
● When an agent competes with another agent to optimise the output, it is said to be in a competitive environment.
● Chess is a competitive game in which the agents compete against one another to win the game, which is the output.
● When numerous agents work together to generate the required result, the agent is said to be in a collaborative environment.
● When many self-driving cars are discovered on the road, they work together to avoid collisions and arrive at their planned destination.
Single-agent vs Multi-agent
● A single-agent environment is defined as one in which there is just one agent.
● A single-agent system is exemplified by a person who is left alone in a maze.
● A multi-agent environment is one in which there are multiple agents.
● Football is a multi-agent sport since each team has 11 players.
Dynamic vs Static
● Dynamic refers to an environment that changes constantly while the agent is engaged in some action.
● A roller coaster ride is dynamic since it is set in motion and the surroundings changes at all times.
● A static environment is one that is idle and does not modify its state.
● When an agent enters a vacant house, there is no change in the surroundings.
Discrete vs Continuous
● A discrete environment is one in which there are a finite number of actions that can be deliberated in the environment to produce the output.
● Chess is a discrete game since it has a limited number of moves. The amount of moves varies from game to game, but it is always finite.
● Continuous refers to an environment in which actions cannot be numbered, i.e. it is not discrete.
● Self-driving cars are an example of continuous environments as their actions are driving, parking, etc. which cannot be numbered.
Q15) Describe a local search algorithm?
A15) Local search algorithms
A local search algorithm completes its task by traversing on a single current node rather than multiple paths and following the neighbours of that node generally.
Although local search algorithms are not systematic, still they have the following two advantages:
● Local search algorithms use a very little or constant amount of memory as they operate only on a single path.
● Most often, they find a reasonable solution in large or infinite state spaces where the classical or systematic algorithms do not work.
Working of a Local search algorithm
Consider the below state-space landscape having both:
● Location: It is defined by the state.
● Elevation: It is defined by the value of the objective function or heuristic cost function.
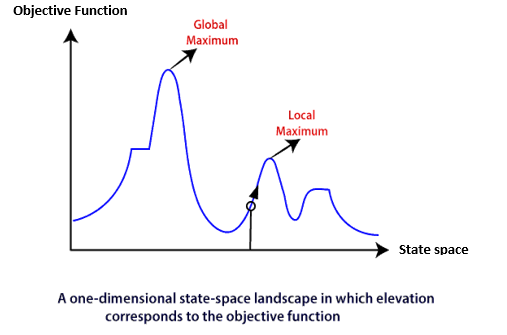
The local search algorithm explores the above landscape by finding the following two points:
● Global Minimum: If the elevation corresponds to the cost, then the task is to find the lowest valley, which is known as Global Minimum.
● Global Maxima: If the elevation corresponds to an objective function, then it finds the highest peak which is called as Global Maxima. It is the highest point in the valley.
Some different types of local searches:
● Hill-climbing Search
● Simulated Annealing
● Local Beam Search
Note: Local search algorithms do not burden to remember all the nodes in the memory; it operates on complete state-formulation.
Simulated Annealing
Simulated annealing is similar to the hill climbing algorithm. It works on the current situation. It picks a random move instead of picking the best move. If the move leads to the improvement of the current situation, it is always accepted as a step towards the solution state, else it accepts the move having a probability less than 1.
This search technique was first used in 1980 to solve VLSI layout problems. It is also applied for factory scheduling and other large optimization tasks.
Local Beam Search
Local beam search is quite different from random-restart search. It keeps track of k states instead of just one. It selects k randomly generated states, and expand them at each step. If any state is a goal state, the search stops with success. Else it selects the best k successors from the complete list and repeats the same process.
In random-restart search where each search process runs independently, but in local beam search, the necessary information is shared between the parallel search processes.
Disadvantages of Local Beam search
● This search can suffer from a lack of diversity among the k states.
● It is an expensive version of hill climbing search.
Q16) What is a hill climbing algorithm?
A16) Hill Climbing Algorithm:
Hill climbing search is a local search problem. The purpose of the hill climbing search is to climb a hill and reach the topmost peak/ point of that hill. It is based on the heuristic search technique where the person who is climbing up on the hill estimates the direction which will lead him to the highest peak.
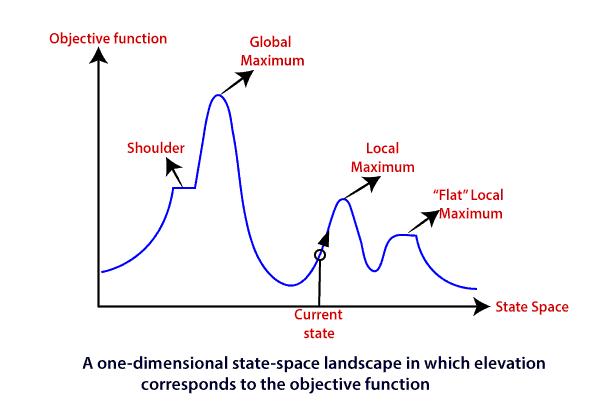
State-space Landscape of Hill climbing algorithm
To understand the concept of hill climbing algorithm, consider the below landscape representing the goal state/peak and the current state of the climber. The topographical regions shown in the figure can be defined as:
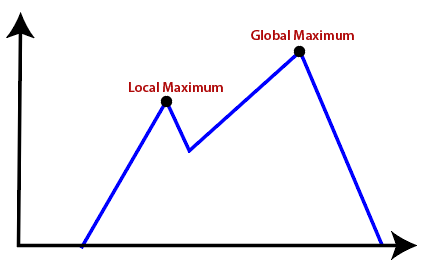
● Global Maximum: It is the highest point on the hill, which is the goal state.
● Local Maximum: It is the peak higher than all other peaks but lower than the global maximum.
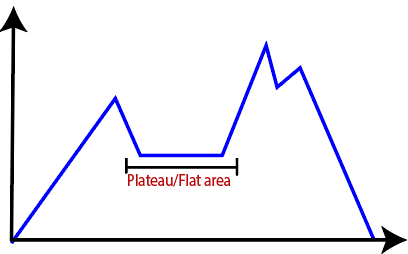
● Flat local maximum: It is the flat area over the hill where it has no uphill or downhill. It is a saturated point of the hill.
● Shoulder: It is also a flat area where the summit is possible.
● Current state: It is the current position of the person.
Q17) What are the types of hill climbing search algorithms?
A17) Types of Hill climbing search algorithm
There are following types of hill-climbing search:
● Simple hill climbing
● Steepest-ascent hill climbing
● Stochastic hill climbing
● Random-restart hill climbing
Simple hill climbing search
Simple hill climbing is the simplest technique to climb a hill. The task is to reach the highest peak of the mountain. Here, the movement of the climber depends on his move/steps. If he finds his next step better than the previous one, he continues to move else remain in the same state. This search focus only on his previous and next step.
Simple hill climbing Algorithm
- Create a CURRENT node, NEIGHBOUR node, and a GOAL node.
- If the CURRENT node=GOAL node, return GOAL and terminate the search.
- Else CURRENT node<= NEIGHBOUR node, move ahead.
- Loop until the goal is not reached or a point is not found.
Steepest-ascent hill climbing
Steepest-ascent hill climbing is different from simple hill climbing search. Unlike simple hill climbing search, It considers all the successive nodes, compares them, and choose the node which is closest to the solution. Steepest hill climbing search is similar to best-first search because it focuses on each node instead of one.
Note: Both simple, as well as steepest-ascent hill climbing search, fails when there is no closer node.
Steepest-ascent hill climbing algorithm
- Create a CURRENT node and a GOAL node.
- If the CURRENT node=GOAL node, return GOAL and terminate the search.
- Loop until a better node is not found to reach the solution.
- If there is any better successor node present, expand it.
- When the GOAL is attained, return GOAL and terminate.
Stochastic hill climbing
Stochastic hill climbing does not focus on all the nodes. It selects one node at random and decides whether it should be expanded or search for a better one.
Random-restart hill climbing
Random-restart algorithm is based on try and try strategy. It iteratively searches the node and selects the best one at each step until the goal is not found. The success depends most commonly on the shape of the hill. If there are few plateaus, local maxima, and ridges, it becomes easy to reach the destination.
Q18) Write the limitations of the hill climbing algorithm?
A18) Limitations of Hill climbing algorithm
Hill climbing algorithm is a fast and furious approach. It finds the solution state rapidly because it is quite easy to improve a bad state. But, there are following limitations of this search:
● Local Maxima: It is that peak of the mountain which is highest than all its neighbouring states but lower than the global maxima. It is not the goal peak because there is another peak higher than it.
● Plateau: It is a flat surface area where no uphill exists. It becomes difficult for the climber to decide that in which direction he should move to reach the goal point. Sometimes, the person gets lost in the flat area.
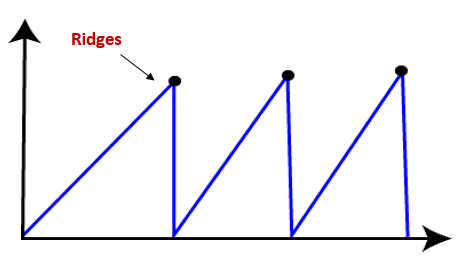
● Ridges: It is a challenging problem where the person finds two or more local maxima of the same height commonly. It becomes difficult for the person to navigate the right point and stuck to that point itself.
Q19) Write the difference between uninformed and informed search?
A19) Difference between uninformed and informed search
Informed Search | Uninformed Search |
It uses knowledge for the searching process. | It doesn’t use knowledge for searching process. |
It finds solution more quickly. | It finds solution slow as compared to informed search. |
It may or may not be complete. | It is always complete. |
Cost is low. | Cost is high. |
It consumes less time. | It consumes moderate time. |
It provides the direction regarding the solution. | No suggestion is given regarding the solution in it. |
It is less lengthy while implementation. | It is more lengthy while implementation. |
Greedy Search, A* Search, Graph Search | Depth First Search, Breadth First Search |
Q20) Write the difference between breadth first search and depth first search?
A20) Difference between Breadth first search and Depth first search
Sr. No. | Key | BFS | DFS |
1 | Definition | BFS, stands for Breadth First Search. | DFS, stands for Depth First Search. |
2 | Data structure | BFS uses Queue to find the shortest path. | DFS uses Stack to find the shortest path. |
3 | Source | BFS is better when target is closer to Source. | DFS is better when target is far from source. |
4 | Suitability for decision tree | As BFS considers all neighbour so it is not suitable for decision tree used in puzzle games. | DFS is more suitable for decision tree. As with one decision, we need to traverse further to augment the decision. If we reach the conclusion, we won. |
5 | Speed | BFS is slower than DFS. | DFS is faster than BFS. |
6 | Time Complexity | Time Complexity of BFS = O(V+E) where V is vertices and E is edges. | Time Complexity of DFS is also O(V+E) where V is vertices and E is edges. |