Unit - 4

Knowledge

Q1) What do you mean by knowledge based agents?

A1) An intelligent agent needs knowledge of the real world in order to make effective decisions and reasoning.

●      Knowledge-based agents are capable of retaining an internal state of knowledge, reasoning about it, updating it in response to observations, and acting on it. These agents can represent the world and operate intelligently using some type of formal representation.

●       Two major components make up knowledge-based agents:

○       Knowledge-base and

○       Inference system.

The following tasks must be performed by a knowledge-based agent:

●       Agents should be able to represent states, actions, and other things.

●       A representative new percept should be able to be incorporated.

●       The internal representation of the world can be updated by an agent.

●       The internal representation of the world can be deduced by an agent.

●       An agent can deduce the best course of action.

The Architecture of knowledge-based agents

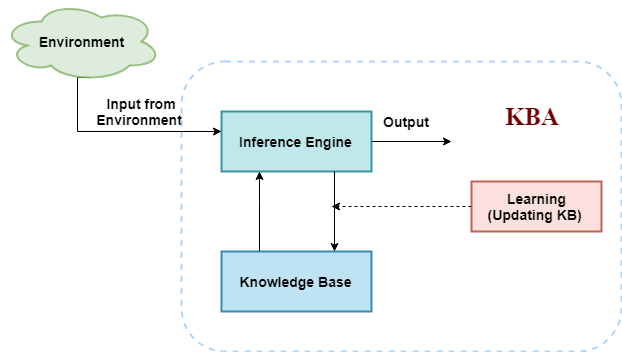
Fig 1: Architecture of knowledge-based agents

The graphic above shows a general design for a knowledge-based agent. The knowledge-based agent (KBA) collects input from the environment by monitoring it. The agent's inference engine processes the data and communicates with KB to make judgments based on the knowledge contained in KB. The learning component of KBA keeps the knowledge base current by learning new material.

Q2) Describe the wumpus world?

A2) The Wumpus world is a basic world example that demonstrates the value of a knowledge-based agent and how knowledge representation is represented. It was inspired by Gregory Yob's 1973 video game Hunt the Wumpus.

The Wumpus world is a cave with four rooms and pathways connecting them. As a result, there are a total of 16 rooms that are interconnected. We now have a knowledge-based AI capable of progressing in this world. There is an area in the cave with a beast named Wumpus who eats everybody who enters. The agent can shoot the Wumpus, but he only has a single arrow. There are some Pits chambers in the Wumpus universe that are bottomless, and if an agent falls into one, he will be stuck there indefinitely.

The intriguing thing about this cave is that there is a chance of finding a gold heap in one of the rooms. So the agent's mission is to find the gold and get out of the cave without getting eaten by Wumpus or falling into Pits. If the agent returns with gold, he will be rewarded, but if he is devoured by Wumpus or falls into the pit, he will be penalised.

A sample diagram for portraying the Wumpus planet is shown below. It depicts some rooms with Pits, one room with Wumpus, and one agent in the world's (1, 1) square position.

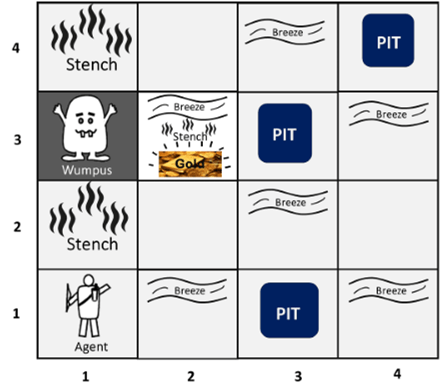
There are some elements that can assist the agent in navigating the cave. The following are the components:

●      The rooms adjacent to the Wumpus room are stinky, thus there is a stench there.

●      The room next to PITs has a breeze, so if the agent gets close enough to PIT, he will feel it.

●      If and only if the room contains gold, there will be glitter.

●      If the agent is facing the Wumpus, the agent can kill it, and the Wumpus will cry horribly, which can be heard throughout the cave.

PEAS description of Wumpus world:

Performance Measures, Environment, Actuators, and Sensors (PEAS) are acronyms for Performance Measures, Environment, Actuators, and Sensors. The PEAS description aids in the classification of the agents.

The Wumpus World problem has the following PEAS description:

Performance measures:

●      Agent gets the gold and return back safe = +1000 points

●      Agent dies = -1000 points

●      Each move of the agent = -1 point

●      Agent uses the arrow = -10 points

Environment:

●      There are 16(4x4) rooms in this cave.

●      The rooms opposite to the Wumpus (not diagonally) stink.

●      Rooms adjacent to the pit (but not diagonally) are cool.

●      The gold-studded chamber gleams.

●      Agent's first position is in Room[1, 1], facing the right side.

●      Wumpus, gold, and the three pits can be found anywhere except in Room[1, 1].

Actuators:

Devices that enable the agent to carry out the operations listed below in the surroundings.

●      Move forward

●      Turn right

●      Turn left

●      Shoot

●      Grab

●      Release

Sensors:

Devices that assist the agent in detecting the following from their surroundings.

●      Breeze

●      Stench

●      Glitter

●      Scream (When the Wumpus is killed)

●      Bump (when the agent hits a wall)

Q3) Write the property of wumpus world?

A3) The Wumpus world Properties:

●      Partially observable: Because the agent can only observe the immediate environment, such as a nearby room, the Wumpus universe is only partially visible.

●      Deterministic: It is deterministic since the world's consequence and outcome are already known.

●      Sequential: It is sequential because the order is critical.

●      Static: Wumpus and Pits aren't moving, thus it's static.

●      Discrete: The setting is distinct.

●      One agent: We only have one agent, and Wumpus is not regarded as an agent, hence the environment is single agent.

Q4) Define logic?

A4) A logic is a formal language that allows sound inference and has well defined syntax and semantics. There are various logics that allow you to represent various types of things and allow for more or less efficient inference. Different varieties of logic exist, such as propositional logic, predicate logic, temporal logic, and description logic. However, expressing something in logic may not be natural, and conclusions may be ineffective.

Example of logic

Language of numerical constraints:

●      A sentence:

x + 3 ≤ z x,

z - variable symbols (primitives in the language)

●      An interpretation:

I:   x = 5, z = 2

Variables mapped to specific real numbers

●      Valuation (meaning) function V:

V (x + 3 ≤ z, I) is False for I: x = 5, z = 2

Is True for I: x = 5, z = 10

Fig 2: Logic

Types of logic

●      Different types of logics possible

●      Propositional logic

●      First-order logic

●      Temporal logic

●      Numerical constraints logic

●      Map-coloring logic

Q5) Describe propositional logic?

A5) Propositional logic (PL) is the simplest form of logic where all the statements are made by propositions. A proposition is a declarative statement which is either true or false. It is a technique of knowledge representation in logical and mathematical form.

Example:

1. a) It is Sunday.  
2. b) The Sun rises from West (False proposition)  
3. c) 3+3= 7(False proposition)  
4. d) 5 is a prime number.   

Following are some basic facts about propositional logic:

●        Propositional logic is also called Boolean logic as it works on 0 and 1.

●        In propositional logic, we use symbolic variables to represent the logic, and we can use any symbol for a representing a proposition, such A, B, C, P, Q, R, etc.

●        Propositions can be either true or false, but it cannot be both.

●        Propositional logic consists of an object, relations or function, and logical connectives.

●        These connectives are also called logical operators.

●        The propositions and connectives are the basic elements of the propositional logic.

●        Connectives can be said as a logical operator which connects two sentences.

●        A proposition formula which is always true is called tautology, and it is also called a valid sentence.

●        A proposition formula which is always false is called Contradiction.

●        A proposition formula which has both true and false values is called

●        Statements which are questions, commands, or opinions are not propositions such as "Where is Rohini", "How are you", "What is your name", are not propositions.

Syntax of propositional logic:

The syntax of propositional logic defines the allowable sentences for the knowledge representation. There are two types of Propositions:

1. Atomic Propositions
2. Compound propositions

1. Atomic Proposition: Atomic propositions are the simple propositions. It consists of a single proposition symbol. These are the sentences which must be either true or false.

Example:

1. a) 2+2 is 4, it is an atomic proposition as it is a true fact.  
2. b) "The Sun is cold" is also a proposition as it is a false fact.   

2. Compound proposition: Compound propositions are constructed by combining simpler or atomic propositions, using parenthesis and logical connectives.

Example:

1. a) "It is raining today, and street is wet."  
2. b) "Ankit is a doctor, and his clinic is in Mumbai."   

Logical Connectives:

Logical connectives are used to connect two simpler propositions or representing a sentence logically. We can create compound propositions with the help of logical connectives. There are mainly five connectives, which are given as follows:

1. Negation: A sentence such as ¬ P is called negation of P. A literal can be either Positive literal or negative literal.
2. Conjunction: A sentence which has ∧connective such as, P ∧ Q is called a conjunction.
   Example: Rohan is intelligent and hardworking. It can be written as,
   P= Rohan is intelligent, Q= Rohan is hardworking. → P∧ Q.
3. Disjunction: A sentence which has ∨ connective, such as P ∨ Q. Is called disjunction, where P and Q are the propositions.

Example: "Ritika is a doctor or Engineer",

Here P= Ritika is Doctor. Q= Ritika is Doctor, so we can write it as P ∨ Q.

4.     Implication: A sentence such as P → Q, is called an implication. Implications are also known as if-then rules. It can be represented as

If it is raining, then the street is wet.

Let P= It is raining, and Q= Street is wet, so it is represented as P → Q

5.     Biconditional: A sentence such as P⇔ Q is a Biconditional sentence, example If I am breathing, then I am alive

P= I am breathing, Q= I am alive, it can be represented as P ⇔ Q.

Following is the summarized table for Propositional Logic Connectives:

Connective symbols	Word	Technical term	Example
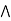	AND	Conjunction	A 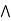B
∨	OR	Disjunction	A∨B
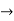	Implies	Implication	AB
⟺	If and only if	Biconditional	A⟺B
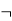Or	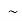Not	Negation	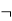Aor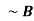

Truth Table:

In propositional logic, we need to know the truth values of propositions in all possible scenarios. We can combine all the possible combination with logical connectives, and the representation of these combinations in a tabular format is called Truth table. Following are the truth table for all logical connectives:

For negation

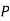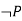True	False
False	True

For conjunction

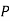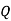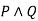True	True	True
True	False	False
False	True	False
False	False	False

For disjunction

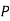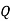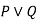True	True	True
False	True	True
True	False	True
False	False	False

For implication

P	Q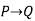
True	True	True
True	False	False
False	True	True
False	False	True

For Biconditional

Truth table with three propositions:

We can build a proposition composing three propositions P, Q, and R. This truth table is made-up of 8n Tuples as we have taken three proposition symbols.

P	Q	R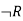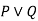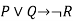
True	True	True	False	True	False
True	True	False	True	True	True
True	False	True	False	True	False
True	False	False	True	True	True
False	True	True	False	True	False
False	True	False	True	True	True
False	False	True	False	False	True
False	False	False	True	False	True

Precedence of connectives:

Just like arithmetic operators, there is a precedence order for propositional connectors or logical operators. This order should be followed while evaluating a propositional problem. Following is the list of the precedence order for operators:

Note: For better understanding use parenthesis to make sure of the correct interpretations. Such as ¬R∨ Q, It can be interpreted as (¬R) ∨ Q.

Logical equivalence:

Logical equivalence is one of the features of propositional logic. Two propositions are said to be logically equivalent if and only if the columns in the truth table are identical to each other.

Let's take two propositions A and B, so for logical equivalence, we can write it as A⇔B. In below truth table we can see that column for ¬A∨ B and A→B, are identical hence A is Equivalent to B

A	B
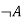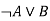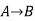T	T	F	T	T
T	F	F	F	F
F	T	T	T	T
F	F	T	T	T

Properties of Operators:

Commutativity:

• P∧ Q= Q ∧ P, or
• P ∨ Q = Q ∨ P.

Associativity:

• (P ∧ Q) ∧ R= P ∧ (Q ∧ R),
• (P ∨ Q) ∨ R= P ∨ (Q ∨ R)

Identity element:

• P ∧ True = P,
• P ∨ True= True.

Distributive:

• P∧ (Q ∨ R) = (P ∧ Q) ∨ (P ∧ R).
• P ∨ (Q ∧ R) = (P ∨ Q) ∧ (P ∨ R).

DE Morgan's Law:

• ¬ (P ∧ Q) = (¬P) ∨ (¬Q)
• ¬ (P ∨ Q) = (¬ P) ∧ (¬Q).

Double-negation elimination:

• ¬ (¬P) = P.

Limitations of Propositional logic:

●        We cannot represent relations like ALL, some, or none with propositional logic.

Example:

All the girls are intelligent.

Some apples are sweet.

●        Propositional logic has limited expressive power.

●        In propositional logic, we cannot describe statements in terms of their properties or logical relationships.

Q6) Explain propositional theorem proving?

A6) Using logical principles of inference to produce logical implications is an alternative method to using logic to solve problems.

This can be less work than model-checking (creating a truth table) or even SAT solving in some circumstances.

Furthermore, logical inference rules are at the level of logical reasoning that humans deliberately strive for.

Entailment is a topic of interest in theorem-proving; for example, given a logical sentence A and a logical phrase B, we can ask if A entails B.

The main notion is that sentence A is what the agent already knows, and sentence B is what the agent can deduce from what it already knows.

The complete "brain" of an agent could be encoded in logic in sentence A.

The deduction theorem is a fundamental fact in logic that states:

If and only if A => B (A implies B) is a tautology, A entails B. (i.e. valid for all assignments of values to its variables).

Such that we can respond to the question "Does A imply B?" by demonstrating that the phrase A => B is a tautology

Remember that a phrase is unsatisfiable if it cannot be made true by assigning values to its variables.

So A => B is a tautology, then !(A=>B) is unsatisfiable, and !(A=>B) == !(!(A & !B)) == A & !B.

As a result, we can rewrite the deduction theorem as follows:

If and only if, A &!B is unsatisfactory, A entails B.

This means you can figure out entailment using a SAT solver!

Rules of Inference

Remember that proofs, or chains of accurate inferences, can be created using a variety of inference procedures.

Modus ponens, for example, is an inference rule that states:

A, A => B

---------   modus ponens

B

This rule states that if you're given a sentence A and a sentence A => B, you can infer B. For example, and-elimination is a set of rules that states:

A & B

-----       and-elimination

A

A & B

-----

B

These two rules encode the (obvious!) fact that if the sentences A and B are both true, then A and B are both true.

Inference rules can also be used to express logical equivalences, such as:

A <==> B

---------------

(A=>B) & (B=>A)

There are many different inference rules, and selecting an acceptable set of rules for a theorem-prover is crucial.

●      The application of a rule of inference can be thought of as an action taken on the state of the world, in which the rule of inference adds more facts to the knowledge base.

●      If there are several inference rules to pick from, knowledge (i.e. heuristics) is required to assist in the decision-making process.

○      Alternatively, we could use backtracking, which entails picking a rule at random, applying it, and continuing until it "appears" that no proof is being achieved.

●      Furthermore, how do we know that the inference rules we're employing are complete, i.e., how do we know that if a proof exists, our set of inference rules will locate it?

○      Is it enough to prove any entailment in propositional logic if the two and-elimination rules are our only rules of inference?

■      no!

■      for example, (P | P) -> P is clearly true, but and-elimination doesn’t apply to this sentence

Q7) Write the effectiveness of propositional model checking?

A7) Given a fixed propositional vocabulary, the collection of viable models is small, hence entailment can be checked by enumerating models. Backtracking and local search methods are two efficient model-checking inference algorithms for propositional logic that can typically solve enormous problems fast.

Based on model checking, there are two families of methods addressing the SAT problem:

a. Based on backtracking

b. Based on local hill-climbing search

1. A complete backtracking algorithm

David-Putnam algorithm (DPLL):

Function DPLL-SATISFIABLE?(s) returns true or false

Inputs: s, a sentence in propositional logic

Clauses 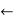the set of clauses in the CNF representation of s

Symbols 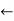a list of  the proposition symbols in s

Return DPLL (clauses, symbols, {})

Function DPLL (clauses, symbols, model) returns true or false

If every clause in clauses is true in model then return true

If some clause in clauses in clauses is false in model then return false

P, value 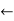FIND-UNIT-CLAUSE (clauses, model)

If P is non-null then return DPLL (clauses, symbols – P, model ∪ {P=value} )

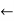P FIRST(symbols): rest REST(symbols)

Return DPLL(clauses, rest, model ∪ {P=true}) or

DPLL(clauses, rest, model ∪ {P=true})

DPLL algorithm for checking satisfiability of a sentence in propositional logic.

DPLL incorporates three enhancements over the TT-ENTAILS scheme: Early termination, pure symbol heuristic, and unit clause heuristic are all examples of heuristics.

Component analysis, variable and value ordering, intelligent backtracking, random restarts, and creative indexing are some of the tricks that SAT solvers use to scale up to huge problems.

Local search algorithms

Local search techniques can be easily applied to the SAT issue if the appropriate evaluation function is used. (An evaluation function that counts the amount of unsatisfied clauses can be used.)

These algorithms work by flipping the truth value of one symbol at a time in the space of full assignments.

Local minima are common in space, and escaping them necessitates various sorts of randomization.

WALKSAT and other local search methods can be utilised to identify solutions. These algorithms are sound, but they aren't complete.

WALKSAT: is one of the most basic and successful algorithms available.

Function WALKSAT (clauses, p, max, flips) returns a satisfying model or failure

Inputs: clauses, a set of clauses in propositional logic

p, the probability of choosing to do a “random walk” move, typically around 0.5

Max, flips, number of flips allowed before giving up

Model a random assignment of true/false to the symbols in clauses

For i=1 to max flips do

If model satisfies clauses then return model

Clause a randomly selected clause from clauses that is false in model

With probability p flip the value in model of a randomly selected symbol from      clause

Else flip whichever symbol in clause maximizes the number of satisfied clauses

Return failure

This is the WALKSAT algorithm for checking satisfiability by randomly flipping the value of variables

Every iteration, the algorithm selects an unsatisfied sentence and alternates between two methods for selecting a symbol to flip:

Either a. a "min-conflicts" step that reduces the number of unsatisfied clauses in the new state; or b. a "min-conflicts" step that reduces the number of unsatisfied clauses in the new state.

Alternatively, there is a "random walk" step that selects the symbol at random.

The input sentence is satisfied when the algorithm returns a model.

There are two possible reasons for the algorithm's failure:

Either a. The sentence is unsatisfiable;

Or b. We need to give the algorithm more time.

If we set max_flips=∞, p>0, the algorithm will:

Either a. If a model exists, eventually return it

Alternatively, b. If the statement is unsatisfactory, never end it.

As a result, WALKSAT is useful when we assume a solution but are unable to detect unsatisfiability.

The landscape of random SAT problems

When looking at satisfiability problems in CNF, an under constrained problem is one that has a small number of clauses confining the variables.

An issue that is over constrained has a large number of clauses compared to the number of variables and is likely to have no solutions.

The notation CNFk(m, n) denotes a k-CNF sentence with m clauses and n symbols. (with n variables and k literals per clause).

Given a set of random sentences, choose clauses consistently, independently, and without replacement from among those clauses with k distinct literals that are either positive or negative at random.

Hardness: problems right at the threshold > over constrained problems > under constrained problems

Fig 3: (a) graph showing the probability that random 3-CNF sentence with n = 50 symbols is satisfiable. (b) graph of the median run time on random 3-CNF sentences.

Satisfiability threshold conjecture: According to one hypothesis, there is a threshold ratio rk for any k3, such that when n approaches infinity, the likelihood that CNFk(n, rn) is satisfiable becomes 1 for all values or r below the threshold, and 0 for all values or r beyond the threshold.

Q8) What is an agent based on propositional logic?

A8) 1. The current state of the world

To avoid contradiction, we can link propositions to timestamps.

e.g. ¬ Stench, Stench

Fluent - Fluently refers to a changing aspect of the world. (For example, Ltx,y)

Atemporal variables - Symbols that represent eternal characteristics of the world do not require a time superscript.

Effect Axioms - define the result of an action at the following time step.

Frame problem - Because the effect axioms fail to define what remains unchanged as a result of an action, significant information is lost.

Solution: explicitly assert all the premises that remain the same by adding frame axioms.

Representation frame problem: In a universe with m distinct actions and n fluents, the proliferation of frame axioms is inefficient; the set of frame axioms will be O(mn).

Solution: Because the world is mobile, there is a solution (for humans each action typically changes no more than some number k of those fluents.) Instead of using a collection of axioms of size O(mk), define the transition model with a set of axioms of size O(mn).

Inferential frame problem: The difficulty of projecting the consequences of a t-step lan of action forward in time O(kt) rather than O(kt) (nt).

Solution: Change your focus from writing axioms about actions to writing axioms about fluents as a solution.

We'll have an axiom for each fluent F that describes the truth value of Ft+1 in terms of fluents at time t and possible actions at time t.

The truth value of Ft+1 can be set in one of 2 ways:

Either a. At time t, the action causes F to be true at time t+1.

Or b. F was already true at time t, and the activity at time t did not change that.

A successor-state axiom is a type of axiom that has the following schema:

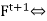Action causes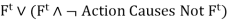

Qualification problem: Specifying any exceptional exceptions that could result in the action failing.

2. A hybrid agent

Hybrid agent: mixes condition-action rules and problem-solving algorithms to determine various aspects of the state of the world.

As a current plan, the agent maintains and updates KB.

The atemporal axioms are found in the first KB. (Don't rely on t.)

Each time step adds a new percept sentence, as well as all the axioms that are dependent on t. (such as the successor-state axioms).

The agent then employs logical inference by ASKING the KB questions (to work out which squares are safe and which have yet to be visited).

The agent program's main body creates a plan based on a diminishing priority of goals:

1. If there is a glint, devise a strategy for grabbing the gold, returning to the original place, and climbing out of the cave;

2. If there is no current plan, plan a route (using A* search) to the nearest safe square that has not yet been visited, ensuring that the path passes through only safe squares;

3. If there are no safe squares to investigate and you still have an arrow, try shooting at one of the available wumpus spots to create a safe square.

4. If this doesn't work, look for a square to explore that isn't shown to be dangerous.

5. If the job is difficult because there is no such square, return to the original spot and climb out of the cave.

Function HYBRID-WUMPUS_AGENT(percept) returns an action

Inputs: percept, a list, [stench, breeze, glitter, bump, scream]

Persisten: KB, a knowledge base, initially the atemporal “wumpus physics” t,  a counter, initially 0, indicating time plan, an action sequence, initially empty

TELL(KB, MAKE-PERCEPT-SENTENCE(percept, t))

TELL the KB the temporal “physics” sentences for time t

Safe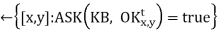

If ASK(KB, Glittert)=true then

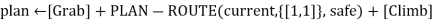
If plan is empty then

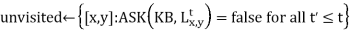
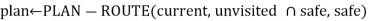
If plan is empty and ASK(KB, HaveArro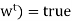 then

Possible_wumpus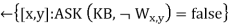

Plan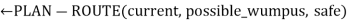

If plan is empty then  //no choice but to take a risk

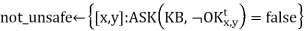
Plan 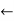 PLAN-ROUTE(current, unvisited ∩ not-unsafe, safe)

If plan is empty then

Plan 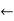 PLAN-ROUTE(current, {[1,1]}, safe) +[Climb]

Action

TELL(KB, MAKE-ACTION-SENTENCE(action, t))

Return action

Function PLAN_ROUTE(current, goals, allowed) returns  an action sequence

Inputs: currents, the agent’s current position

Goals, a set of squares; try to plan a route to one of them

Allowed,  a set of squares that can form part of the route

Problem ROUTE-PROBLEM (current, goals, allowed) (problem)

Return - GRAPH-SEARCH (problem)

This is the hybrid agent program for the wumpus world.

Weakness: The computational expense goes up as time goes by.

3. Logical state estimation

To maintain a consistent update time, we must cache the inference result.

Belief state: Some representation of the set of all current world states that could exist. (used to replace the previous history of percepts and all of its repercussions.)

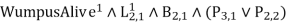
The proposition symbols linked with the current time step and the temporal symbols are used in a logical phrase.

Maintaining a logical statement that represents the set of probable states consistent with the observation history is required for logical state estimation. Each update step necessitates inference using the environment's transition model, which is comprised of successor-state axioms that define how each fluent changes.

State estimation: The process of updating one's belief state as new information becomes available.

Exact state estimation may necessitate logical formulations with exponentially increasing symbol counts.

One typical method for approximating state estimation is to characterise belief states as literal conjunctions (1-CNF formulas).

Given the belief state at t-1, the agent simply tries to prove Xt and Xt for each symbol Xt.

The new belief state is formed by the conjunction of verifiable literals, and the previous belief state is discarded.

(As time passes, this scheme may lose some information.)

Given the whole percept history, the set of feasible states represented by the 1-CNF belief state comprises all states that are in fact possible. The 1-CNF belief state serves as a conservative approximation or outer envelope.

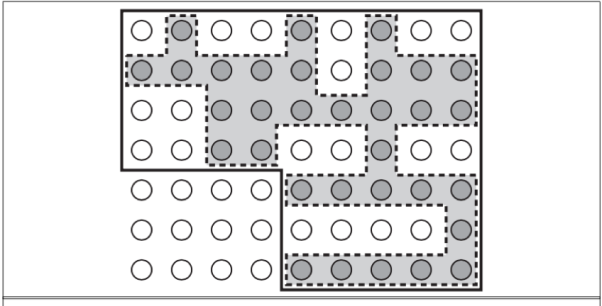
Fig 4: Depiction of 1-CNF belief state as a simply representable, conservative approximation to the exact belief state.

4. Making plans by propositional inference

Instead of using A* search, we can develop plans using logical inference.

Basic idea:

1. Make a sentence that incorporates the following elements:

a) Init0: a set of statements about the initial state; b) Init1: a set of assertions about the initial state; c) Init2:

b) Transition1,..., Transitiont: The successor-state axioms for all feasible actions at each time interval up to a maximum time interval t;

c) Have Goldt Climbed Outt: The claim that the goal has been reached at time t.

2. Use a SAT solver to complete the sentence. The aim can be achieved if the solver discovers a satisfying model; else, planning is impossible.

3. Assuming you've established a model, extract the variables that describe actions and set them to true.

They constitute a strategy for achieving the objectives when taken together.

SAT solution, or identifying feasible models detailing future action sequences that meet the objective, can be used to make decisions within a logical agent. This method only works in totally visible or sensor-free environments.

SATPLAN: is an acronym for "propositional planning." (Cannot be used in an environment that is just partially visible.

SATPLAN looks for models in a sentence that includes the beginning state, aim, successor-state axioms, and action exclusion axioms.

(Because the agent has no idea how many steps it will take to attain the goal, the algorithm tries every number of steps t up to some maximum plausible plan length Tmax.)

Function SATPLAN(init, transition, goal, returns solution or failure

Inputs: init, transition, goal, constitute a description of the problem

an upper limit for plan length

For t=0 t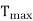o do

Cnf TRANSLATE-TO-SAT(init, transition, goat, t)

Model SAT-SOLVER(cnf)

If model is null then

Return EXTRACT-SOLUTION(model)

Return failure

This is the SATPlan algorithm.

Precondition axioms: added to avoid creating plans containing illegal actions, saying that an action occurrence requires the preconditions to be satisfied.

Action exclusion axioms were included to prevent the formation of plans that had many simultaneous activities that interfered with one another.

Because it lacks the expressive power to deal concisely with time, space, and universal patterns of relationships among things, propositional logic does not scale to unbounded settings.

Q9) Describe first order logic?

A9) In the topic of Propositional logic, we have seen how to represent statements using propositional logic. But unfortunately, in propositional logic, we can only represent the facts, which are either true or false. PL is not sufficient to represent complex sentences or natural language statements. The propositional logic has very limited expressive power. Consider the following sentence, which we cannot represent using PL logic.

●        "Some humans are intelligent", or

●        "Sachin likes cricket."

To represent the above statements, PL logic is not sufficient, so we required some more powerful logic, such as first-order logic.

First-Order logic:

●        First-order logic is another way of knowledge representation in artificial intelligence. It is an extension to propositional logic.

●        FOL is sufficiently expressive to represent the natural language statements in a concise way.

●        First-order logic is also known as Predicate logic or First-order predicate logic. First-order logic is a powerful language that develops information about the objects in a more easy way and can also express the relationship between those objects.

●        First-order logic (like natural language) does not only assume that the world contains facts like propositional logic but also assumes the following things in the world:

• Objects: A, B, people, numbers, colors, wars, theories, squares, pits, wumpus, ......
• Relations: It can be unary relation such as: red, round, is adjacent, or n-any relation such as: the sister of, brother of, has color, comes between
• Function: Father of, best friend, third inning of, end of, ......

●        As a natural language, first-order logic also has two main parts:

• Syntax
• Semantics

Syntax of First-Order logic:

The syntax of FOL determines which collection of symbols is a logical expression in first-order logic. The basic syntactic elements of first-order logic are symbols. We write statements in short-hand notation in FOL.

Basic Elements of First-order logic:

Following are the basic elements of FOL syntax:

Atomic sentences:

●        Atomic sentences are the most basic sentences of first-order logic. These sentences are formed from a predicate symbol followed by a parenthesis with a sequence of terms.

●        We can represent atomic sentences as Predicate (term1, term2, ......, term n).

Example: Ravi and Ajay are brothers: => Brothers(Ravi, Ajay).

Chinky is a cat: => cat (Chinky).

Complex Sentences:

●        Complex sentences are made by combining atomic sentences using connectives.

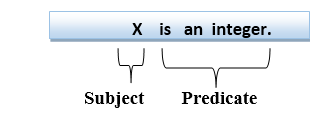
First-order logic statements can be divided into two parts:

●        Subject: Subject is the main part of the statement.

●        Predicate: A predicate can be defined as a relation, which binds two atoms together in a statement.

Consider the statement: "x is an integer.", it consists of two parts, the first part x is the subject of the statement and second part "is an integer," is known as a predicate.

Properties of Quantifiers:

●        In universal quantifier, ∀x∀y is similar to ∀y∀x.

●        In Existential quantifier, ∃x∃y is similar to ∃y∃x.

●        ∃x∀y is not similar to ∀y∃x.

Q10) Write about quantifier in first order logic?

A10) Quantifiers in First-order logic:

●        A quantifier is a language element which generates quantification, and quantification specifies the quantity of specimen in the universe of discourse.

●        These are the symbols that permit to determine or identify the range and scope of the variable in the logical expression. There are two types of quantifier:

1. Universal Quantifier, (for all, everyone, everything)
2. Existential quantifier, (for some, at least one).

Universal Quantifier:

Universal quantifier is a symbol of logical representation, which specifies that the statement within its range is true for everything or every instance of a particular thing.

The Universal quantifier is represented by a symbol ∀, which resembles an inverted A.

Note: In universal quantifier we use implication "→".

If x is a variable, then ∀x is read as:

●        For all x

●        For each x

●        For every x.

Example:

All man drink coffee.

Let a variable x which refers to a cat so all x can be represented in UOD as below:

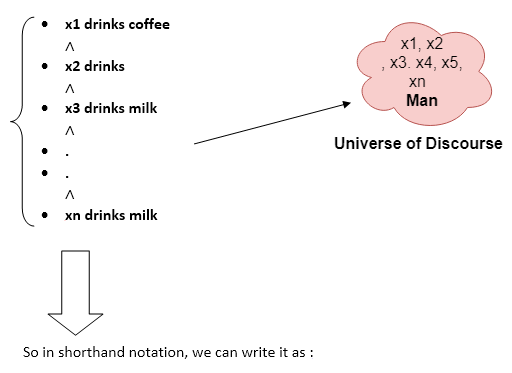
∀x man(x) → drink (x, coffee).

It will be read as: There are all x where x is a man who drink coffee.

Existential Quantifier:

Existential quantifiers are the type of quantifiers, which express that the statement within its scope is true for at least one instance of something.

It is denoted by the logical operator ∃, which resembles as inverted E. When it is used with a predicate variable then it is called as an existential quantifier.

Note: In Existential quantifier we always use AND or Conjunction symbol (∧).

If x is a variable, then existential quantifier will be ∃x or ∃(x). And it will be read as:

●        There exists a 'x.'

●        For some 'x.'

●        For at least one 'x.'

Example:

Some boys are intelligent.

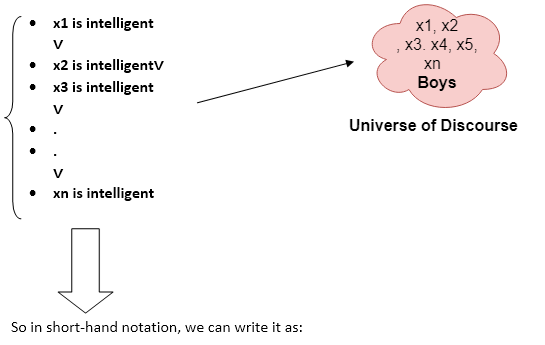
∃x: boys(x) ∧ intelligent(x)

It will be read as: There are some x where x is a boy who is intelligent.

Points to remember:

●        The main connective for universal quantifier ∀ is implication →.

●        The main connective for existential quantifier ∃ is and ∧.

Q11) Write some example of FOl using quantifier?

A11) Some Examples of FOL using quantifier:

1. All birds fly.

In this question the predicate is "fly(bird)."

And since there are all birds who fly so it will be represented as follows.

∀x bird(x) →fly(x).

2. Every man respects his parent.

In this question, the predicate is "respect(x, y)," where x=man, and y= parent.

Since there is every man so will use ∀, and it will be represented as follows:

∀x man(x) → respects (x, parent).

3. Some boys play cricket.

In this question, the predicate is "play(x, y)," where x= boys, and y= game. Since

There are some boys so we will use ∃, and it will be represented as:

∃x boys(x) → play(x, cricket).

4. Not all students like both Mathematics and Science.

In this question, the predicate is "like(x, y)," where x= student, and y= subject.

Since there are not all students, so we will use ∀ with negation, so following representation for this:

¬∀ (x) [ student(x) → like(x, Mathematics) ∧ like(x, Science)].

5. Only one student failed in Mathematics.

In this question, the predicate is "failed(x, y)," where x= student, and y= subject.
Since there is only one student who failed in Mathematics, so we will use following representation for this:

∃(x) [ student(x) → failed (x, Mathematics) ∧∀ (y) [¬(x==y) ∧ student(y) → ¬failed (x, Mathematics)].

Free and Bound Variables:

The quantifiers interact with variables which appear in a suitable way. There are two types of variables in First-order logic which are given below:

Free Variable: A variable is said to be a free variable in a formula if it occurs outside the scope of the quantifier.

Example: ∀x ∃(y)[P (x, y, z)], where z is a free variable.

Bound Variable: A variable is said to be a bound variable in a formula if it occurs within the scope of the quantifier.

Example: ∀x [A (x) B( y)], here x and y are the bound variables.

Q12) What do you mean by representation revisited?

A12) Programming languages (such as C++, Java, and Lisp) are by far the most widely used formal languages.

This procedural method contrasts with propositional logic's declarative character, in which knowledge and inference are separated and inference is domain-independent.

They lack the expressiveness required to deal with incomplete data.

●      Using disjunction and negation, propositional logic has enough expressive capability to deal with partial knowledge.

●      Compositionality is a third characteristic of propositional logic that is useful in representation languages.

The meaning of a sentence in a compositional language is determined by the meaning of its constituent elements.

For example, ―S1,4 ^ S1,2‖ is related to the meanings of ―S1,4‖ and ―S1,2‖.

Propositional logic lacks the expressive power to succinctly explain a complex environment with numerous items.

For example, we were compelled to establish a distinct regulation for each square regarding breezes and pits, such as

B 1,1⇔(P 1,2 or P 2,1)

In English, though, it seems simple enough to state unequivocally that squares near to pits are airy.

Natural languages are also non-compositional, in the sense that the meaning of a statement like "Then she saw it" might be influenced by the context created by numerous preceding and following sentences.

Finally, natural languages contain ambiguity, which can make thinking harder.

The following are the most obvious features of natural language syntax:

●      Object-referential nouns and noun phrases ( squares , pits, wumpuses ).

●      Verbs and verb phrases that allude to object relationships (is breezy, is adjacent to, shoots).

●      Some of these relationships are functions, meaning they have only one value for each input. It's simple to start a list of objects, relations, and functions:

Objects: People, houses, numbers, theories, Ronald McDonald, colors, baseball games, wars, centuries….

Relation: These can be unary relations or properties like red, round, bogus, prime, multi-storied............, or more general n-ary relations like brother of, bigger than, within, part of, has colour, happened after, owns, comes between, etc.

Functions: father of, closest friend, third inning of, more than, and the start of.

●      The first-order logic language has a syntax and semantics based on objects and relations.

●      First-order logic can also be used to convey facts about some or all of the universe's items.

●      This allows generic laws or norms to be represented, such as the sentence "Squares adjacent to the Wumpus are stinky."

The ontological commitment made by each language—that is, what it assumes about the nature of reality—is the basic difference between propositional and first-order logic.

●      Propositional logic, for example, assumes that there are facts in the world that either hold or do not hold. There are two possible states for each fact: true or untrue.

●      Temporal logic assumes that facts are true at specific moments and that those times (which can be points or intervals) are in chronological sequence.

Higher-order logic considers the first-order logic's relations and functions to be objects in and of themselves. This enables claims to be made about all object relations. A talent for dealing with logical notation is required of an AI student.

Language	Ontological Commitment (What exists in the world)	Epistemological Commitment (What an agent believes about facts)
Propositional logic	Facts	True/false/unknown
First-order logic	Facts, objects, relations	True/false/unknown
Temporal logic	Facts, objects, relations, times	True/false/unknown
Probability theory	Facts	Degree of belief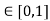
Fuzzy logic	Facts with degree of truth	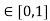Known interval value

Table 9: Formal language and their ontological and epistemological commitments

Q13) Explain the syntax of first order logic?

A13) First-order logic is a type of knowledge representation used in artificial intelligence. It's a propositional logic variation.

• FOL is expressive enough to convey natural language statements in a concise manner.
• First-order logic is sometimes known as predicate logic or first-order predicate logic. First-order logic is a complex language for constructing information about objects and expressing relationships between them.
• First-order logic (as does natural language) assumes not just that the world contains facts, as propositional logic does, but also that the world has the following:

○      Objects: People, numbers, colors, conflicts, theories, squares, pits, wumpus,

○      Relation: It can be a unary relation like red, round, or nearby, or an n-any relation like sister of, brother of, has color, or comes between.

○      Functions: Father of, best friend, third inning of, last inning of......

• First-order logic contains two basic pieces as a natural language:

○      Syntax

○      Semantics

Syntax

Syntax has to do with what ‘things’ (symbols, notations) one is allowed to use in the language and in what way; there is/are a(n):

●       Alphabet

●       Language constructs

●       Sentences to assert knowledge

Logical connectives (⇒, ∧, ∨, and ⇐⇒), negation (¬), and parentheses. These will be used to recursively build complex formulas, just as was done for propositional logic.

Constants symbols are strings that will be interpreted as representing objects, e.g., Bob might be a constant.

Variable symbols will be used as “place holders” for quantifying over objects.

Predicate symbols Each has an arity (number of arguments) associated with it, which can be zero or some other finite value. Predicates will be used to represent object characteristics and relationships.

Zero-arity Because predicate symbols are viewed as propositions in first-order logic, propositional logic is subsumed. These assertions can be thought of as world properties.

Predicates with a single parameter can be thought of as specifying object attributes. If Rich is a single-arity predicate, then Rich (Bob) is used to indicate that Bob is wealthy. Multi-arity predicates are used to describe relationships between items.

Formula 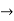   PrimitiveFormula

| (Formula Connective Formula)

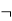|  Sentence

| Qualifier Variable Formula

PrimitiveFormula   Predicate(Term,…,Term)

Term     Function(Term,…,Term)

| Constant

| Variable

Connectifier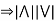   

Quantifier  

Constant   any string that is not used as a variable predicate or function

Variable   any string that is not used as a constant predicate or function

Predicate   any string that is not used as a constant variable or function

Function   any string that is not used as a constant predicate or constant

Function symbols Each has a specific arity (number of input arguments) and is understood as a function that maps the stated number of input objects to objects. Allowing FatherOf to be a single-arity function symbol, the natural interpretation of FatherOf (Bob) is Bob's father.

Zero-arity function symbols are considered to be constants.

Universal and existential quantifier symbols will be used to quantify over objects. For example, ∀ x Alive(x) ⇒ Breathing(x) is a universally quantified statement that uses the variable x as a placeholder.

Q14) What is the semantics of first order logic?

A14) Semantics of First-Order Logic

As with all logics, the first step in determining the semantics of first-order logic is to define the models of first-order logic. Remember that one of the benefits of using first-order logic is that it allows us to freely discuss objects and their relationships. As a result, our models will comprise objects as well as information about their properties and interactions with other items.

First order model

A first-order model is a tuple hD, Ii, where D denotes a non-empty object domain and I denote an interpretation function. D is nothing more than a collection of items or elements that can be finite, infinite, or uncountable. The interpretation function I gives each of the available constant, function, and predicate symbols a meaning or interpretation as follows:

• If c is a constant symbol, then I(c) is an object in D. Thus, given a model, a constant can be viewed as naming an object in the domain.
• If f is a function symbol of arity n, then I(f) is a total function from Dn to D. That is the interpretation of f is a function that maps n domain objects to the domain D.
• If p is a predicate symbol of arity n > 0, then I(p) is a subset of Dn; that is, a predicate symbol is interpreted as a set of tuples from the domain. If a tuple O = (o1, · · · , on) is in I(p) then we say that p is true for the object tuple O.
• If p is a predicate symbol of arity 0, i.e., a simple proposition, then I(p) is equal to either true or false.

Assume we have a single predicate TallerThan, a single function FatherOf, and a single constant Bob. The following could be a model M1 for these symbols:

D = {BOB, JON, NULL}

I(Bob) = BOB

I(TallerThan) = {hBOB, JONi}

Because I(FatherOf) is a function, we'll only show the value for each argument to give the FatherOf meaning.

I(FatherOf)(BOB) = JON

I(FatherOf)(JON) = NULL

I(FatherOf)(NULL) = NULL

M2 could also be interpreted as follows,

D = { BOB, JON }

I(Bob) = BOB

I(TallerThan) = { hBOB, JONi,hJON, BOBi }

I(FatherOf)(BOB) = BOB

I(FatherOf)(JON) = JON

It's vital to highlight the difference between Bob, which is a constant (a syntactic entity), and BOB, which is a domain object (a semantic entity). The second interpretation isn't exactly what we're looking for (the objects are dads of themselves, and TallerThan is inconsistent), but it's still a viable model. By imposing proper limitations on the symbols, the knowledge base can rule out such unexpected models from consideration.

Q15) Describe knowledge engineering in first order logic?

A15) Inference is used in First-Order Logic to generate new facts or sentences from current ones. It's crucial to understand some basic FOL terms before diving into the FOL inference rule.

Substitution:

Substitution is a fundamental approach for modifying phrases and formulations. All first-order logic inference systems contain it. The substitution becomes more difficult when there are quantifiers in FOL. We refer to the replacement of a constant "a" for the variable "x" when we write F[a/x].

Equality:

Atomic sentences are generated in First-Order Logic not only through the employment of predicate and words, but also through the application of equality. We can do this by using equality symbols, which indicate that the two terms relate to the same thing.

FOL inference rules for quantifier:

Because inference rules in first-order logic are comparable to those in propositional logic, below are some basic inference rules in FOL:

●       Universal Generalization

●       Universal Instantiation

●       Existential Instantiation

●       Existential introduction

Universal Generalization:

• Universal generalization is a valid inference rule that states that if premise P(c) is true for any arbitrary element c in the universe of discourse, we can arrive at the conclusion x P. (x).
• It can be represented as:
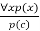
• If we want to prove that every element has a similar property, we can apply this rule.
• x must not be used as a free variable in this rule.

Example: Let's represent, P(c): "A byte contains 8 bits", so for ∀ x P(x) "All bytes contain 8 bits.", it will also be true.

Universal Instantiation:

• Universal instantiation, often known as universal elimination or UI, is a valid inference rule. It can be used numerous times to add more sentences.
• The new knowledge base is logically equivalent to the previous one.
• We can infer any phrase by replacing a ground word for the variable, according to the UI.
• According to the UI rule, any phrase P(c) can be inferred by substituting a ground term c (a constant inside domain x) for any object in the universe of discourse in x P(x).
• It can be represented as:

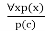
Example: IF "Every person like ice-cream"=> ∀x P(x) so we can infer that

"John likes ice-cream" => P(c)

Existential Instantiation:

• Existential Elimination, also known as Existential Instantiation, is a valid first-order logic inference rule.
• It can only be used once to substitute for the existential sentence.
• Despite the fact that the new KB is not conceptually identical to the previous KB, it will suffice if the old KB was.
• This rule states that one can infer P(c) from the formula given in the form of ∃x P(x) for a new constant symbol c.
• The only constraint with this rule is that c must be a new word for which P(c) is true.
• It can be represented as:

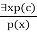
Existential introduction

• An existential generalization, also known as an existential introduction, is a valid inference rule in first-order logic.
• If some element c in the world of discourse has the characteristic P, we can infer that something else in the universe has the attribute P, according to this rule.
• It can be represented as:

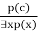
Example: Let's say that,

"Pritisha got good marks in English."

"Therefore, someone got good marks in English."

Propositional vs. First-Order Inference

Previously, inference in first order logic was checked via propositionalization, which is the act of turning the Knowledge Base included in first order logic into propositional logic and then utilizing any of the propositional logic inference mechanisms to check inference.

Q16) Write the difference between propositional logic and first order logic?

A16) Key differences between PL and FOL

●      Propositional Logic converts a complete sentence into a symbol and makes it logical whereas in First-Order Logic relation of a particular sentence will be made that involves relations, constants, functions, and constants.

●      The limitation of PL is that it does not represent any individual entities whereas FOL can easily represent the individual establishment that means if you are writing a single sentence then it can be easily represented in FOL.

●      PL does not signify or express the generalization, specialization or pattern for example ‘QUANTIFIERS’ cannot be used in PL but in FOL users can easily use quantifiers as it does express the generalization, specialization, and pattern.

Q17) Write the difference between propositional logic and predicate logic?

A17) Difference between propositional logic and predicate logic