Unit - 5

Reasoning

Q1) What do you mean by inference in first order logic?

A1) Inference in First-Order Logic is used to deduce new facts or sentences from existing sentences. Before understanding the FOL inference rule, let's understand some basic terminologies used in FOL.

Substitution:

Substitution is a fundamental operation performed on terms and formulas. It occurs in all inference systems in first-order logic. The substitution is complex in the presence of quantifiers in FOL. If we write F[a/x], so it refers to substitute a constant "a" in place of variable "x".

Note: First-order logic is capable of expressing facts about some or all objects in the universe.

Equality:

First-Order logic does not only use predicate and terms for making atomic sentences but also uses another way, which is equality in FOL. For this, we can use equality symbols which specify that the two terms refer to the same object.

Example: Brother (John) = Smith.

As in the above example, the object referred by the Brother (John) is similar to the object referred by Smith. The equality symbol can also be used with negation to represent that two terms are not the same objects.

Example: ￢(x=y) which is equivalent to x ≠y.

FOL inference rules for quantifier:

As propositional logic we also have inference rules in first-order logic, so following are some basic inference rules in FOL:

●        Universal Generalization

●        Universal Instantiation

●        Existential Instantiation

●        Existential introduction

1. Universal Generalization:

●        Universal generalization is a valid inference rule which states that if premise P(c) is true for any arbitrary element c in the universe of discourse, then we can have a conclusion as ∀ x P(x).

●        It can be represented as: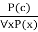

●        This rule can be used if we want to show that every element has a similar property.

●        In this rule, x must not appear as a free variable.

Example: Let's represent, P(c): "A byte contains 8 bits", so for ∀ x P(x) "All bytes contain 8 bits.", it will also be true.

2. Universal Instantiation:

●        Universal instantiation is also called as universal elimination or UI is a valid inference rule. It can be applied multiple times to add new sentences.

●        The new KB is logically equivalent to the previous KB.

●        As per UI, we can infer any sentence obtained by substituting a ground term for the variable.

●        The UI rule state that we can infer any sentence P(c) by substituting a ground term c (a constant within domain x) from ∀ x P(x) for any object in the universe of discourse.

●        It can be represented as:.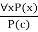

Example:1.

IF "Every person like ice-cream"=> ∀x P(x) so we can infer that

"John likes ice-cream" => P(c)

Example: 2.

Let's take a famous example,

"All kings who are greedy are Evil." So let our knowledge base contains this detail as in the form of FOL:

∀x king(x) ∧ greedy (x) → Evil (x),

So from this information, we can infer any of the following statements using

Universal Instantiation:

●        King(John) ∧ Greedy (John) → Evil (John),

●        King(Richard) ∧ Greedy (Richard) → Evil (Richard),

●        King(Father(John)) ∧ Greedy (Father(John)) → Evil (Father(John)),

3. Existential Instantiation:

●        Existential instantiation is also called as Existential Elimination, which is a valid inference rule in first-order logic.

●        It can be applied only once to replace the existential sentence.

●        The new KB is not logically equivalent to old KB, but it will be satisfiable if old KB was satisfiable.

●        This rule states that one can infer P(c) from the formula given in the form of ∃x P(x) for a new constant symbol c.

●        The restriction with this rule is that c used in the rule must be a new term for which P(c ) is true.

●        It can be represented as: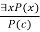

Example:

From the given sentence: ∃x Crown(x) ∧ OnHead(x, John),

So we can infer: Crown(K) ∧ OnHead( K, John), as long as K does not appear in the knowledge base.

●        The above used K is a constant symbol, which is called Skolem constant.

●        The Existential instantiation is a special case of Skolemization process.

4. Existential introduction

●        An existential introduction is also known as an existential generalization, which is a valid inference rule in first-order logic.

●        This rule states that if there is some element c in the universe of discourse which has a property P, then we can infer that there exists something in the universe which has the property P.

●        It can be represented as: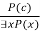

●        Example: Let's say that,

"Priyanka got good marks in English."

"Therefore, someone got good marks in English."

Q2) Compare propositional and first order logic?

A2) Propositional vs. First-Order Inference

Previously, inference in first order logic was checked via propositionalization, which is the act of turning the Knowledge Base included in first order logic into propositional logic and then utilizing any of the propositional logic inference mechanisms to check inference.

Inference rules for quantifiers:

To get sentences without quantifiers, several inference techniques can be applied to sentences containing quantifiers. We'll be able to make the conversion if we follow these requirements.

Universal Instantiation (UI):

The rule states that by substituting a ground word (a term without variables) for the variable, we can deduce any sentence. Let SUBST () stand for the outcome of the substitution on the sentence a. The rule is then written.

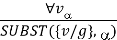
For any v and g ground term combinations. For example, in the knowledge base, there is a statement that states that all greedy rulers are Evil.

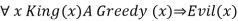
For the variable x, with the substitutions like {x/John}, {x/Richard} the following sentences can be inferred

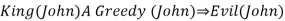
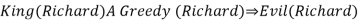
As a result, the set of all potential instantiations can be used to substitute a globally quantified phrase.

Existential Instantiation (EI):

The existential statement states that there is some object that fulfills a requirement, and that the instantiation process is simply giving that object a name that does not already belong to another object. A Skolem constant is the moniker given to this new name. Existential Instantiation is a subset of a broader process known as "skolemization."

If the statement a, variable v, and constant symbol k do not occur anywhere else in the knowledge base,

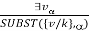
For example, from the sentence

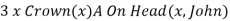
So we can infer the sentence

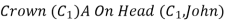
As long as C1 does not appear elsewhere in the knowledge base. Thus, an existentially quantified sentence can be replaced by one instantiation

Elimination of Universal and Existential quantifiers should give new knowledge base which can be shown to be inferentially equivalent to old in the sense that it is satisfiable exactly when the original knowledge base is satisfiable.

Q3) Explain unification?

A3) Unification is the process of finding a substitute that makes two separate logical atomic expressions identical. The substitution process is necessary for unification.

• It accepts two literals as input and uses substitution to make them identical.
• Let Ψ1 and Ψ2 be two atomic sentences and 𝜎 be a unifier such that, Ψ1𝜎 = Ψ2𝜎, then it can be expressed as UNIFY (Ψ1, Ψ2).
• Example: Find the MGU for Unify {King(x), King (John)}

Let Ψ1 = King(x), Ψ2 = King (John),

Substitution θ = {John/x} is a unifier for these atoms, and both phrases will be identical after this replacement.

• For unification, the UNIFY algorithm is employed, which takes two atomic statements and returns a unifier for each of them (If any exist).
• All first-order inference techniques rely heavily on unification.
• If the expressions do not match, the result is failure.
• The replacement variables are referred to as MGU (Most General Unifier).

Example: Let's say there are two different expressions, P (x, y), and P (a, f(z)).

In this example, we need to make both above statements identical to each other. For this, we will perform the substitution.

P (x, y)......... (i)

P (a, f(z))......... (ii)

• Substitute x with a, and y with f(z) in the first expression, and it will be represented as a/x and f(z)/y.
• With both the substitutions, the first expression will be identical to the second expression and the substitution set will be: [a/x, f(z)/y].

Conditions for Unification:

The following are some fundamental requirements for unification:

• Atoms or expressions with various predicate symbols can never be united since they have different predicate symbols.
• Both phrases must have the same number of arguments.
• If two comparable variables appear in the same expression, unification will fail.

Generalized Modus Ponens:

For atomic sentences pi, pi ', and q, where there is a substitution θ such that SU θ, pi) = SUBST (θ, pi '), for all i

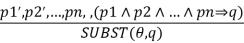
N + 1 premises = N atomic sentences + one implication. Applying SUBST (θ, q) yields the conclusion we seek.

p1’ = King (John)   p2’ = Greedy(y)

p1 = King(x)   p2 = Greedy(x)

θ = {x / John, y/ John}  q = Evil(x)

SUBST (θ, q) is Evil (John)

Generalized Modus Ponens = lifted Modus Ponens

Lifted - transformed from:

Propositional Logic → First-order Logic

Unification Algorithms

Algorithm: Unify (L1, L2)

1. If L1 or L2 are both variables or constants, then:

1. If L1 and L2 are identical, then return NIL.

2. Else if L1 is a variable, then if L1 occurs in L2 then return {FAIL}, else return (L2/L1).

3. Also, Else if L2 is a variable, then if L2 occurs in L1 then return {FAIL}, else return (L1/L2). d. Else return {FAIL}.

2. If the initial predicate symbols in L1 and L2 are not identical, then return {FAIL}.

3. If LI and L2 have a different number of arguments, then return {FAIL}.

4. Set SUBST to NIL. (At the end of this procedure, SUBST will contain all the substitutions used to unify L1 and L2.)

5. For I ← 1 to the number of arguments in L1:

1. Call Unify with the ith argument of L1 and the ith argument of L2, putting the result in S.

2. If S contains FAIL, then return {FAIL}.

3. If S is not equal to NIL, then:

2. Apply S to the remainder of both L1 and L2.

3. SUBST: = APPEND (S, SUBST).

6. Return SUBST.

Q4) Define first order inferences?

A4) Inference in first order logic was checked via propositionalization, which is the act of turning the Knowledge Base included in first order logic into propositional logic and then utilizing any of the propositional logic inference mechanisms to check inference.

Inference rules for quantifiers:

To get sentences without quantifiers, several inference techniques can be applied to sentences containing quantifiers. We'll be able to make the conversion if we follow these requirements.

Universal Instantiation (UI):

The rule states that by substituting a ground word (a term without variables) for the variable, we can deduce any sentence. Let SUBST () stand for the outcome of the substitution on the sentence a. The rule is then written.

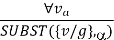
For any v and g ground term combinations. For example, in the knowledge base, there is a statement that states that all greedy rulers are Evil.

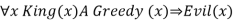
For the variable x, with the substitutions like {x/John},{x/Richard}the following sentences can be inferred

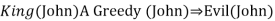
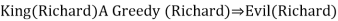
As a result, the set of all potential instantiations can be used to substitute a globally quantified phrase.

Existential Instantiation (EI):

The existential statement states that there is some object that fulfills a requirement, and that the instantiation process is simply giving that object a name that does not already belong to another object. A Skolem constant is the moniker given to this new name. Existential Instantiation is a subset of a broader process known as "skolemization."

If the statement a, variable v, and constant symbol k do not occur anywhere else in the knowledge base,

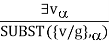
For example, from the sentence

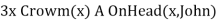
So we can infer the sentence

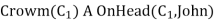
As long as C1 does not appear elsewhere in the knowledge base. Thus an existentially quantified sentence can be replaced by one instantiation

Elimination of Universal and Existential quantifiers should give new knowledge base which can be shown to be inferentially equivalent to old in the sense that it is satisfiable exactly when the original knowledge base is satisfiable.

Q5) Define forward chaining?

A5) Forward chaining is also known as forward deduction or forward reasoning when using an inference engine. Forward chaining is a method of reasoning that begins with atomic sentences in a knowledge base and uses inference rules to extract more information in the forward direction until a goal is reached.

Beginning with known facts, the Forward-chaining algorithm activates all rules with satisfied premises and adds their conclusion to the known facts. This procedure is repeated until the problem is resolved.

It's a method of inference that starts with sentences in the knowledge base and generates new conclusions that may then be utilized to construct subsequent inferences. It's a plan based on data. We start with known facts and organize or chain them to get to the query. The ponens modus operandi is used. It begins with the data that is already accessible and then uses inference rules to extract new data until the goal is achieved.

Example: To determine the color of Fritz, a pet who croaks and eats flies, for example. The Knowledge Base contains the following rules:

If X croaks and eats flies — → Then X is a frog.

If X sings — → Then X is a bird.

If X is a frog — → Then X is green.

If x is a bird — -> Then X is blue.

In the KB, croaks and eating insects are found. As a result, we arrive at rule 1, which has an antecedent that matches our facts. The KB is updated to reflect the outcome of rule 1, which is that X is a frog. The KB is reviewed again, and rule 3 is chosen because its antecedent (X is a frog) corresponds to our newly confirmed evidence. The new result is then recorded in the knowledge base (i.e., X is green). As a result, we were able to determine the pet's color based on the fact that it croaks and eats flies.

Properties of forward chaining

• It is a down-up approach since it moves from bottom to top.
• It is a process for reaching a conclusion based on existing facts or data by beginning at the beginning and working one's way to the end.
• Because it helps us to achieve our goal by exploiting current data, forward-chaining is also known as data-driven.
• The forward-chaining methodology is often used in expert systems, such as CLIPS, business, and production rule systems.

Q6) Write the property of forward chaining?

A6) Properties of forward chaining

• It is a down-up approach since it moves from bottom to top.
• It is a process for reaching a conclusion based on existing facts or data by beginning at the beginning and working one's way to the end.
• Because it helps us to achieve our goal by exploiting current data, forward-chaining is also known as data-driven.
• The forward-chaining methodology is often used in expert systems, such as CLIPS, business, and production rule systems.

Q7) Describe backward chaining?

A7) Backward-chaining is also known as backward deduction or backward reasoning when using an inference engine. A backward chaining algorithm is a style of reasoning that starts with the goal and works backwards through rules to find facts that support it.

It's an inference approach that starts with the goal. We look for implication phrases that will help us reach a conclusion and justify its premises. It is an approach for proving theorems that is goal-oriented.

Example: Fritz, a pet that croaks and eats flies, needs his color determined. The Knowledge Base contains the following rules:

If X croaks and eats flies — → Then X is a frog.

If X sings — → Then X is a bird.

If X is a frog — → Then X is green.

If x is a bird — -> Then X is blue.

The third and fourth rules were chosen because they best fit our goal of determining the color of the pet. For example, X may be green or blue. Both the antecedents of the rules, X is a frog and X is a bird, are added to the target list. The first two rules were chosen because their implications correlate to the newly added goals, namely, X is a frog or X is a bird.

Because the antecedent (If X croaks and eats flies) is true/given, we can derive that Fritz is a frog. If it's a frog, Fritz is green, and if it's a bird, Fritz is blue, completing the goal of determining the pet's color.

Q8) Write the property of backward chaining?

A8) Properties of backward chaining

• A top-down strategy is what it's called.
• Backward-chaining employs the modus ponens inference rule.
• In backward chaining, the goal is broken down into sub-goals or sub-goals to ensure that the facts are true.
• Because a list of objectives decides which rules are chosen and implemented, it's known as a goal-driven strategy.
• The backward-chaining approach is utilized in game theory, automated theorem proving tools, inference engines, proof assistants, and other AI applications.
• The backward-chaining method relied heavily on a depth-first search strategy for proof.

Q9) Describe a resolution?

A9) Resolution is a theorem proving technique that proceeds by building refutation proofs, i.e., proofs by contradictions. It was invented by a Mathematician John Alan Robinson in the year 1965.

Resolution is used, if there are various statements are given, and we need to prove a conclusion of those statements. Unification is a key concept in proofs by resolutions. Resolution is a single inference rule which can efficiently operate on the conjunctive normal form or clausal form.

Clause: Disjunction of literals (an atomic sentence) is called a clause. It is also known as a unit clause.

Conjunctive Normal Form: A sentence represented as a conjunction of clauses is said to be conjunctive normal form or CNF.

The resolution inference rule:

The resolution rule for first-order logic is simply a lifted version of the propositional rule. Resolution can resolve two clauses if they contain complementary literals, which are assumed to be standardized apart so that they share no variables.

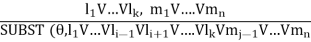
Where li and mj are complementary literals.

This rule is also called the binary resolution rule because it only resolves exactly two literals.

Example:

We can resolve two clauses which are given below:

[Animal (g(x) V Loves (f(x), x)] and [￢ Loves(a, b) V ￢Kills(a, b)]

Where two complimentary literals are: Loves (f(x), x) and ￢ Loves (a, b)

These literals can be unified with unifier θ= [a/f(x), and b/x], and it will generate a resolvent clause:

[Animal (g(x) V ￢ Kills(f(x), x)].

Steps for Resolution:

1. Conversion of facts into first-order logic.
2. Convert FOL statements into CNF
3. Negate the statement which needs to prove (proof by contradiction)
4. Draw resolution graph (unification).

To better understand all the above steps, we will take an example in which we will apply resolution.

Example:

John likes all kind of food.

Apple and vegetable are food

Anything anyone eats and not killed is food.

Anil eats peanuts and still alive

1. Harry eats everything that Anil eats.

Prove by resolution that:

John likes peanuts.

Step-1: Conversion of Facts into FOL

In the first step we will convert all the given statements into its first order logic.

a.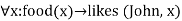

b.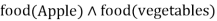

c.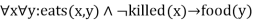

d.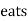

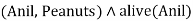
e.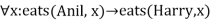

f.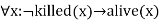

g.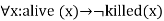

h.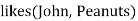

Here f and g are added predicates.

Step-2: Conversion of FOL into CNF

In First order logic resolution, it is required to convert the FOL into CNF as CNF form makes easier for resolution proofs.

Eliminate all implication (→) and rewrite

1. ∀x ¬ food(x) V likes(John, x)
2. Food(Apple) Λ food(vegetables)
3. ∀x ∀y ¬ [eats(x, y) Λ¬ killed(x)] V food(y)
4. Eats (Anil, Peanuts) Λ alive(Anil)
5. ∀x ¬ eats(Anil, x) V eats(Harry, x)
6. ∀x¬ [¬ killed(x) ] V alive(x)
7. ∀x ¬ alive(x) V ¬ killed(x)
8. Likes(John, Peanuts).

Move negation (¬)inwards and rewrite

9.     ∀x ¬ food(x) V likes(John, x)

10. Food(Apple) Λ food(vegetables)

11. ∀x ∀y ¬ eats(x, y) V killed(x) V food(y)

12. Eats (Anil, Peanuts) Λ alive(Anil)

13. ∀x ¬ eats(Anil, x) V eats(Harry, x)

14. ∀x ¬killed(x) ] V alive(x)

15. ∀x ¬ alive(x) V ¬ killed(x)

16. Likes(John, Peanuts).

Rename variables or standardize variables

17. ∀x ¬ food(x) V likes(John, x)

18. Food(Apple) Λ food(vegetables)

19. ∀y ∀z ¬ eats(y, z) V killed(y) V food(z)

20. Eats (Anil, Peanuts) Λ alive(Anil)

21. ∀w¬ eats(Anil, w) V eats(Harry, w)

22. ∀g ¬killed(g) ] V alive(g)

23. ∀k ¬ alive(k) V ¬ killed(k)

24. Likes(John, Peanuts).

●        Eliminate existential instantiation quantifier by elimination.

In this step, we will eliminate existential quantifier ∃, and this process is known as Skolemization. But in this example problem since there is no existential quantifier so all the statements will remain same in this step.

●        Drop Universal quantifiers.

In this step we will drop all universal quantifier since all the statements are not implicitly quantified so we don't need it.

1. ¬ food(x) V likes(John, x)
2. Food(Apple)
3. Food(vegetables)
4. ¬ eats(y, z) V killed(y) V food(z)
5. Eats (Anil, Peanuts)
6. Alive(Anil)
7. ¬ eats(Anil, w) V eats(Harry, w)
8. Killed(g) V alive(g)
9. ¬ alive(k) V ¬ killed(k)
10. Likes(John, Peanuts).

Note: Statements "food(Apple) Λ food(vegetables)" and "eats (Anil, Peanuts) Λ alive(Anil)" can be written in two separate statements.

●        Distribute conjunction ∧ over disjunction ¬.

This step will not make any change in this problem.

Step-3: Negate the statement to be proved

In this statement, we will apply negation to the conclusion statements, which will be written as ¬likes(John, Peanuts)

Step-4: Draw Resolution graph:

Now in this step, we will solve the problem by resolution tree using substitution. For the above problem, it will be given as follows:

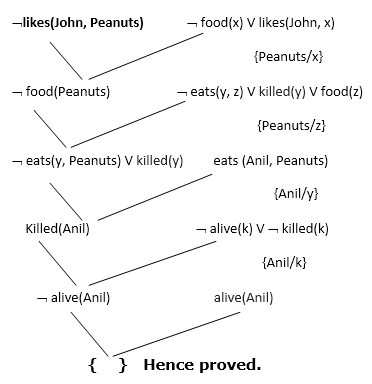
Hence the negation of the conclusion has been proved as a complete contradiction with the given set of statements.

Explanation of Resolution graph:

●        In the first step of resolution graph, ¬likes(John, Peanuts) , and likes(John, x) get resolved(cancelled) by substitution of {Peanuts/x}, and we are left with ¬ food(Peanuts)

●        In the second step of the resolution graph, ¬ food(Peanuts) , and food(z) get resolved (cancelled) by substitution of { Peanuts/z}, and we are left with ¬ eats(y, Peanuts) V killed(y) .

●        In the third step of the resolution graph, ¬ eats(y, Peanuts) and eats (Anil, Peanuts) get resolved by substitution {Anil/y}, and we are left with Killed(Anil) .

●        In the fourth step of the resolution graph, Killed(Anil) and ¬ killed(k) get resolve by substitution {Anil/k}, and we are left with ¬ alive(Anil) .

●        In the last step of the resolution graph ¬ alive(Anil) and alive(Anil) get resolved.

Q10) What do you mean by knowledge representation?

A10) Humans are best at understanding, reasoning, and interpreting knowledge. Humans know things, which is that of the knowledge and as per that of their knowledge they perform several of the actions in that of the real world. But how machines do all of these things come under the knowledge representation and the reasoning. Hence we can describe that of the Knowledge representation as follows they are:

●        Knowledge representation and the reasoning (KR, KRR) is the part of Artificial intelligence which concerned with AI agents thinking and how thinking contributes to intelligent behavior of agents.

●        It is responsible for representing information about the real world so that a computer can understand and then can utilize that of the knowledge to solve that of the complex real world problems for instance diagnosis a medical condition or communicating with humans in natural language.

●        It is also a way which describes that how we can represent that of the knowledge in that of the artificial intelligence. Knowledge representation is not just that of the storing data into some of the database, but it also enables of an intelligent machine to learn from that of the knowledge and experiences so that of the it can behave intelligently like that of a human.

What to Represent:

Following are the kind of knowledge which needs to be represented in that of the AI systems:

●        Object: All the facts about that of the objects in our world domain. Example Guitars contains strings, trumpets are brass instruments.

●        Events: Events are the actions which occur in our world.

●        Performance: It describes that of the behaviour which involves the knowledge about how to do things.

●        Meta-knowledge: It is knowledge about what we know.

●        Facts: Facts are the truths about the real world and what we represent.

●        Knowledge-Base: The central component of the knowledge-based agents is the knowledge base. It is represented as KB. The Knowledgebase is a group of the Sentences (Here, sentences are used as a technical term and not identical with the English language).

Knowledge: Knowledge is the awareness or familiarity gained by that of the experiences of facts, data, and situations. Following are the types of knowledge in artificial intelligence:

The relation between knowledge and intelligence they are as follows:

Knowledge of real-worlds plays a very important role in the intelligence and the same for creating the artificial intelligence. Knowledge plays an important role in that of the demonstrating intelligent behavior in the AI agents. An agent is the only able to accurately act on some of the input when he has some of the knowledge or the experience about that of the input.

Let's suppose if you met some of the person who is speaking in that of a language which you don't know, then how you will able to act on that. The same thing applies to that of the intelligent behavior of the agents.

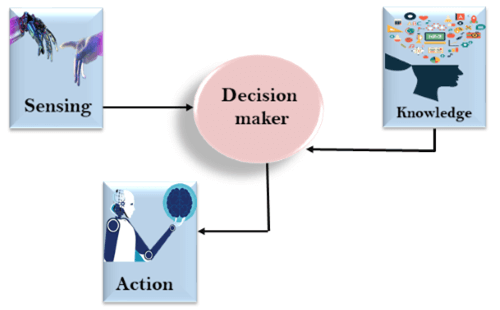
As we can see in below diagram, there is one decision maker which act by sensing that of the environment and using the knowledge. But if the knowledge part will not present then, it cannot display intelligent behavior.

Q11) What are the types of knowledge?

A11) Types of knowledge

Following are the various types of knowledge:

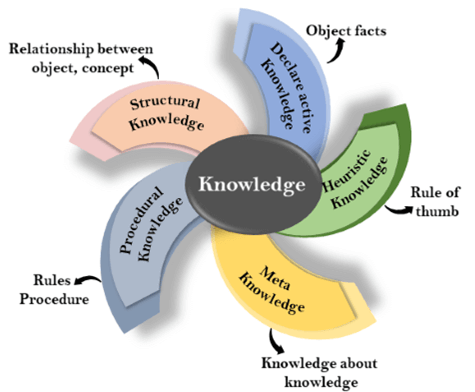
1. Declarative Knowledge:

●        Declarative knowledge is to know about something.

●        It includes the concepts, the facts, and the objects.

●        It is also called descriptive knowledge and expressed in declarative sentences.

●        It is simpler than procedural language.

2. Procedural Knowledge

●        It is also known as imperative knowledge.

●        Procedural knowledge is a type of knowledge which is responsible for knowing how to do something.

●        It can be directly applied to any task.

●        It includes rules, strategies, procedures, agendas, etc.

●        Procedural knowledge depends on the task on which it can be applied.

3. Meta-knowledge:

●        Knowledge about the other types of that of the knowledge is known as Meta-knowledge.

4. Heuristic knowledge:

●        Heuristic knowledge is representing knowledge of some experts in a filed or subject.

●        Heuristic knowledge is the rules of the thumb based on the previous experiences, awareness of the approaches, and which are good to that of the work but not guaranteed.

5. Structural knowledge:

●        Structural knowledge is basic knowledge to problem-solving.

●        It describes relationships between various concepts such as kind of, part of, and grouping of something.

●        It describes the relationship that exists between concepts or objects.

Q12) How to approach knowledge representation?

A12) Approaches to knowledge representation:

There are mainly four approaches to knowledge representation, which are given below:

1. Simple relational knowledge:

●        It is the simplest way of that of the storing facts which uses that of the relational method and each fact about that of a set of the object is set out systematically in that of the columns.

●        This approach of the knowledge representation is famous in the database systems where the relationship between that of the different entities is represented.

●        This approach has little opportunity for that of the inference.

Example: The following is the simple relational knowledge representation.

2.Inheritable knowledge:

●        In the inheritable knowledge approach, all the data must be stored into that of a hierarchy of the classes.

●        All classes should be arranged in that of a generalized form or a hierarchal manner.

●        In this approach, we apply the inheritance property.

●        Elements inherit values from the other members of a class.

●        This approach contains the inheritable knowledge which shows that of a relation between instance and the class, and it is known as instance relation.

●        Every individual frame can represent that of the collection of attributes and its value.

●        In this approach, objects and the values are represented in the Boxed nodes.

●        We use Arrows which point from that of the objects to their values.

Example:

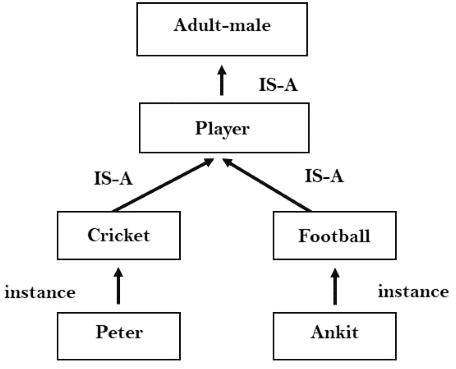
3. Inferential knowledge:

●        Inferential knowledge approach represents the knowledge in the form of the formal logics.

●        This approach can be used to derive more that of the facts.

●        It guaranteed the correctness.

●        Example: Let's suppose there are two statements:

1. Marcus is a man
2. All men are mortal

Then it can represent as;

Man(Marcus)

∀x = man (x) ----------> mortal (x)s

4. Procedural knowledge:

●        Procedural knowledge approach uses that of the small programs and codes which describes how to do specific things, and how to proceed.

●        In this approach, one important rule is used which is If-Then rule.

●        In this knowledge, we can use various coding languages such as LISP language and Prolog language.

●        We can easily represent heuristic or domain-specific knowledge using this approach.

●        But it is not necessary that we can represent all cases in this approach.

Requirements for knowledge Representation system:

A good knowledge representation system must possess the following properties.

1. Representational Accuracy:

KR system should have that of the ability to represent that the all kind of the required knowledge.

2.     Inferential Adequacy:

KR system should have ability to manipulate that of the representational structures to produce that of the new knowledge corresponding to the existing structure.

3.     Inferential Efficiency:

The ability to direct the inferential knowledge mechanism into the most productive directions by storing appropriate guides.

4.     Acquisitioned efficiency- The ability to acquire the new knowledge easily using automatic methods.

Q13) What is AI knowledge cycle?

A13) AI knowledge cycle:

An Artificial intelligence system has that of the following components for displaying intelligent behavior they are as follows:

●        Perception

●        Learning

●        Knowledge Representation and Reasoning

●        Planning

●        Execution

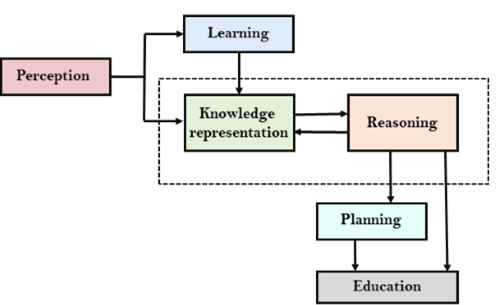
The above diagram is showing how that of an AI system can interacts with that of the real world and what the components help it to show the intelligence. AI system has the Perception component by which it retrieves information from that of its environment. It can be visual, audio or another form of the sensory input. The learning component is that the responsible for learning from data captured by the Perception comportment.

In the complete cycle, the main components are the knowledge representation and the Reasoning. These two components are involved in showing that of the intelligence in machine-like humans. These two components are independent with each other but also coupled together. The planning and execution depend on analysis of that of the Knowledge representation and the reasoning.

Q14) What do you mean by categories and objects?

A14) Categories and Objects

●      Sorting the items into categories.

●      At the level of categories, some reasoning takes happen.

●      "I'd like to eat an apple," says the narrator.

●      Member(x, Apple) and Subset(x, Apple) are Apple(x) and Member(x, Apple) respectively (Apple, Food).

●      The categories create a hierarchy, or simply a network, in which each class inherits the properties of the parent (apples are both food and fruit).

●      A taxonomy is made up of the categories of a class.

The organisation of items into categories is required by KR.

●      Interaction at the object level;

●      Reasoning at the category level

Categories play a role in predictions about objects

●      Based on perceived properties

FOL can represent categories in two ways (First Order Logic)

●      Predicates: apple(x)

●      Reification of categories into objects: apples

Category = set of its members.

Category organization

Relation = inheritance:

●      Food is edible in all forms; fruit is a subclass of food, and apples are a subclass of fruit, hence an apple is edible.

Defines a taxonomy

FOL and categories

●      An object is a member of a category

○      MemberOf(BB12,Basketballs)

●      A category is a subclass of another category

○      SubsetOf(Basketballs,Balls)

●      All members of a category have some properties

○      ∀x (MemberOf(x,Basketballs) ⇒Round(x))

●      All members of a category can be recognized by some properties

○      ∀x  (Orange(x)  ∧Round(x)  ∧Diameter(x) = 9.5in

∧MemberOf(x,Balls)⇒MemberOf(x,BasketBalls))

●      A category as a whole has some properties

○      MemberOf(Dogs,DomesticatedSpecies)

Relations between categories

●      If two or more categories have no members in common, they are disjoint:

○      Disjoint(s)⇔(∀c1,c2 c1 ∈s ∧c2 ∈s ∧c1 ≠ c2 ⇒Intersection(c1,c2) ={})

●      Example: Disjoint({animals, vegetables})

●      If all members of the set are covered by categories in s, a set of categories s represents an exhaustive decomposition of a category c:

○      E.D.(s,c) ⇔(∀i i∈c ⇒∃c2 c2∈s ∧i ∈c2)

●      Example: ExhaustiveDecomposition( {Americans, Canadian, Mexicans},

NorthAmericans).

●      A partition is an exhaustive disjoint decomposition:

○      Partition(s,c) ⇔Disjoint(s) ∧E.D.(s,c)

●      Example: Partition({Males,Females},Persons).

●      Is ({Americans,Canadian, Mexicans},NorthAmericans) a partition?

●      No! There might be dual citizenships.

●      By defining membership criteria that are both necessary and sufficient, categories can be created.

Substances and Objects

The real universe is made up of primitive items (such as atomic particles) and composite objects made up of them.

We can avoid the complexity of dealing with large numbers of primitive things separately by reasoning at the level of large objects like apples and cars.

However, there is a large part of reality that appears to defy any clear individuation—division into different objects.

b∈Butter ∧PartOf(p, b) ⇒p ∈Butter .

We may now say that butter melts at a temperature of roughly 30 degrees Celsius:

b∈Butter ⇒MeltingPoint(b,Centigrade(30))

What's going on is that some properties are intrinsic, meaning they pertain to the thing's very substance rather than the object as a whole.

When you cut a piece of stuffin in half, the fundamental properties—such as density, boiling temperature, flavor, color, ownership, and so on—remain intact.

Extrinsic qualities like as weight, length, and shape, on the other hand, are lost during subdivision.

Stuff is the most broad substance type, with no inherent qualities specified.

Thing is the most broad discrete object category, with no extrinsic attributes specified.

Q15) What are events?

A15) The usefulness of situation calculus is limited: it was created to represent a world in which activities are discrete, instantaneous, and occur one at a time.

Consider filling a bathtub, which is a continual action. Situation calculus can claim that the tub is empty before the action and filled after the action, but it can't describe what happens in the middle of the activity. It also can't depict two simultaneous actions, as cleaning one's teeth while waiting for the tub to fill. We present an alternative formalism known as event calculus to address such circumstances, which is based on points of time rather than situations.

Instances of event categories are used to describe events.4 Shankar's flight from San Francisco to Washington, D.C. Is described as follows:

E1 ∈ Flyings ∧ Flyer (E1, Shankar ) ∧ Origin(E1, SF) ∧ Destination(E1,DC) .

Then we use Happens(E1, I to indicate that the event E1 occurred at the time interval i. A (start, finish) pair of times is used to express time intervals.

For one form of the event calculus, the entire collection of predicates is

T(f, t) Fluent f is true at time t

Happens(e, i) Event e happens over the time interval i

Initiates(e, f, t) Event e causes fluent f to start to hold at time t

Terminates(e, f, t) Event e causes fluent f to cease to hold at time t

Clipped(f, i) Fluent f ceases to be true at some point during time interval i

Restored (f, i) Fluent f becomes true sometime during time interval i

T is defined as a fluent that holds at a given point in time if it was started by an event in the past and was not made false (clipped) by an intervening event.

If an event terminates a fluent and it is not made true (restored) by another event, the fluent is no longer valid. The axioms are as follows:

Happens(e, (t1, t2)) ∧ Initiates(e, f, t1) ∧ ￢Clipped(f, (t1, t)) ∧ t1 < t ⇒T(f, t) Happens(e, (t1, t2)) ∧ Terminates(e, f, t1)∧ ￢Restored (f, (t1, t)) ∧ t1 < t ⇒￢T(f, t)

Where Clipped and Restored are terms used to describe as:

Clipped(f, (t1, t2)) ⇔∃ e, t, t3 Happens(e, (t, t3)) ∧ t1 ≤ t < t2 ∧ Terminates(e, f, t) Restored (f, (t1, t2)) ⇔∃e, t, t3 Happens(e, (t, t3)) ∧ t1 ≤ t < t2 ∧ Initiates(e, f, t)

T can be extended to function over intervals as well as time points; for example, a fluent holds across an interval if it holds at every point within the interval:

T(f, (t1, t2)) ⇔[∀ t (t1 ≤ t < t2) ⇒ T(f, t)]

Q16) Describe mental object and modal logic?

A16) So far, the agents we've created have beliefs and can infer new ones. Despite this, none of them has any understanding of beliefs or deduction. Controlling inference requires understanding of one's own knowledge and reasoning processes.

Propositional attitudes - the way a person feels about mental objects (e.g. Believes, Knows, Wants, Intends, and Informs). These propositional attitudes do not behave in the same way that ordinary predicates do.

To say, for example, that Lois is aware of Superman's ability to fly:

Knows(Lois, CanFly(Superman))

The inferential rules conclude that "Lois knows Clark can fly" if "Superman is Clark Kent" is true (this is an example of referential transparency). Lois, on the other hand, has no idea that Clark can fly.

Superman = Clark

(Superman = Clark) and (Knows(Lois, CanFly(Superman)) ⊨ Knows(Lois, CanFly(Clark))

Referential transparency

●      In whatever situation, an expression always yields the same outcome.

●      For example, if an agent understands that 2+2=4 and 4<5, it should also know that 2+25.

●      integrated into inferential rules in most formal logic languages.

Referential opacity

●      transparent but not referential

●      For propositional attitudes, we want referential opacity because terms matter, and not all agents are aware of which terms are co-referential.

●      In most formal logic languages, this is not directly achievable (except Modal Logic).

Modal Logic

Created to allow for referential opacity in the knowledge base

Regular logic is concerned with a single modality (the truth modality), allowing us to say "P is true."

Modal logic comprises modal operators that use sentences as arguments rather than terms (e.g. "A knows P" is represented with notation KAP where K is the modal operator for knowledge, A is the agent, and P is a sentence).

Modal logic has the same syntax as first-order logic, with the exception that modal operators can also be used to build sentences.

Modal logic's semantics are more sophisticated. A model in first-order logic has a set of objects as well as an interpretation that translates each name to the correct item, relation, or function. We want to be able to consider both the possibility that Superman's secret identity is Clark and the chance that it isn't in modal logic. As a result, a model in modal logic is a collection of possible universes (instead of 1 true world). Accessibility relations connect the worlds in a graph (one relation for each modal operator). If everything in w1 is consistent with what A knows in w0, we say that world w1 is accessible from world w0 with respect to the modal operator KA, and we express this as Acc (KA, w0, w1).

As an arrow between possible universes, the figure depicts accessibility.

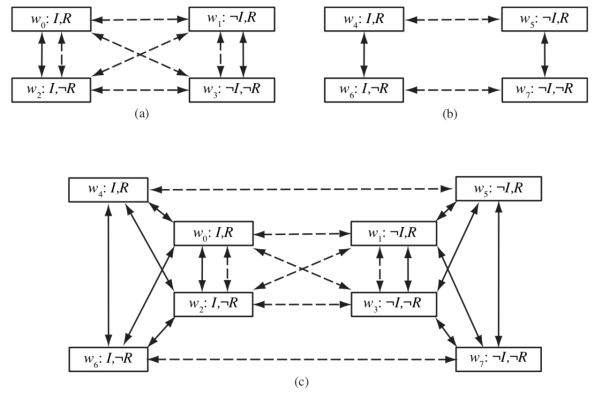
Fig: Possible worlds with accessibility relations KSuperman and KLois .

An atom of knowledge If and only if P is true in every world accessible from w, KAP is true in world w. Recursive application of this rule with the standard laws of first-order logic yields the truth of more complex sentences. That is, modal logic can be used to reason about nested knowledge sentences, or what one agent knows about the knowledge of another agent.

We can claim, for example, that while Lois does not know if Superman's secret identity is Clark Kent, she does know that Clark does:

KLois [KClark Identity(Superman, Clark) ∨ KClark ¬Identity(Superman, Clark)]

The situation depicted in the TOP-LEFT of the picture is one in which Superman knows his own identity and neither he nor Lois has received the weather report. So, in w0, Superman has access to the worlds w0 and w2; rain may or may not be forecast.

For Lois, all four universes are accessible from one another; she has no idea what the report is about or whether Clark is Superman. But she is aware that Superman is aware of whether he is Clark or not, because in every reality accessible to Lois, either Superman is aware of I or he is aware of ¬I. Lois isn't sure which is the case, but she knows Superman is aware of it.

The situation depicted in the top-right corner of the picture is one in which it is widely assumed that Lois has seen the weather report. So she knows it's going to rain in w4 and it's not going to rain in w6. Superman is unaware of the report, but he is aware that Lois is aware of it, because in every reality to which he has access, she either knows R or knows¬ R.

The situation depicted in the BOTTOM of the figure is one in which Superman's identity is widely known, and Lois may or may not have seen the weather report. We show this by combining the two top situations and adding arrows to show that Superman has no idea which one is correct. We don't need to draw any arrows for Lois because she already knows. In w0, Superman still recognises I but not R, and he has no idea whether Lois recognises R. According to what Superman knows, he might be in w0 or w2, in which case Lois is unsure whether R is true, w4, in which case she is aware of R, or w6, in which case she is aware of ¬R.

Modal Logic's Tricky Interplay of Quantifiers and Knowledge

The English line "Bond knows that someone is a spy," for example, is ambiguous.

"There is a certain someone that Bond knows is a spy," says the first reading:

∃x KBondSpy(x)

In modal logic, this indicates that there is an x that Bonds knows to be a spy in all accessible worlds.

The second interpretation is that "Bond just knows that at least one spy exists":

KBond∃x Spy(x)

In modal logic, this indicates that there is an x who is a spy in each accessible world, but it does not have to be the same x in each world.

Modal Logic - Writing Axioms With Modal Operators

State that agents can deduce; "if an agent knows P and recognises that P implies Q, then the agent knows Q."

(KaP ∧ Ka(P ⇒ Q)) ⇒ KaQ

Declare that every agent is aware of the truth or falsity of every proposition P:

Ka(P v ¬P)

True belief is justified knowledge:

KaP ⇒ P

If an agent is aware of something, they are aware that they are aware of it:

KaP ⇒ Ka(KaP)

Similar axioms can be defined for belief (commonly abbreviated as B) and other modal operators.

One issue with modal logic is that it presupposes agents have logical omniscience (that is, if an agent knows a set of axioms, then it knows all consequences of those axioms).

Q17) Write about reasoning system for categories?

A17) The main building blocks of large-scale knowledge representation schemes are categories.

There are two families of systems that are closely related:

Description logics provide a formal language for constructing and combining category definitions, as well as efficient algorithms for deciding subset and superset relationships between categories. Semantic networks provide graphical aids for visualizing a knowledge base and efficient algorithms for inferring properties of an object based on its category membership; and semantic networks provide graphical aids for visualizing a knowledge base and efficient algorithms for inferring properties of an object based on its category membership.

Semantic networks:

In 1909, Charles S. Peirce created existential graphs, a graphical notation of nodes and edges that he dubbed "the logic of the future."

●      Semantic networks come in a variety of shapes and sizes, but they may all represent individual objects, categories of objects, and relationships between things.

●      The names of objects or categories are displayed in ovals or boxes, and they are connected with labeled connections in a standard graphical format.

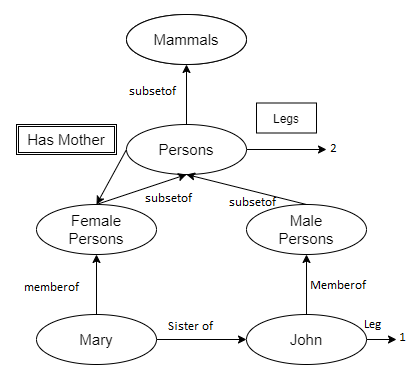
For example, Figure below has a Member Of link between Mary and Female Persons, corresponding to the logical assertion Mary ∈Female Persons; similarly, the Sister Of link between Mary and John corresponds to the assertion Sister Of (Mary, John). We can connect categories using Subset Of links, and so on.

It's easy to get carried away when painting bubbles and arrows.

Can we draw a Has Mother link from Persons to Female Persons, for example, because we know that persons have female persons as mothers?

Has Mother is a relationship between a person and his or her mother, and categories do not have mothers, hence the answer is no.

As a result, in Figure below, we've employed a specific notation—the double-boxed link.

According to this link,

∀x x∈ Persons ⇒ [∀ y HasMother (x, y) ⇒ y ∈ FemalePersons ] .

We might also say that people have two legs—that is, that they have two legs.

∀x x∈ Persons ⇒ Legs(x, 2) .

The single-boxed link in Figure below is used to assert properties for each category member.

One of the key attractions of semantic networks has been the simplicity and effectiveness of this inference process when compared to logical theorem proving.

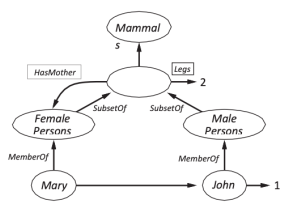
Fig: Semantic network with four objects and four categories. Relations are denoted by labeled links

Inverse linkages are another prominent method of inference. Has Sister, for example, is the inverse of Sister Of, implying that

When compared to first-order logic, the reader may have recognised an evident disadvantage of semantic network notation: the fact that linkages between bubbles only reflect binary relations.

In a semantic network, for example, the sentence Fly(Shankar, New York, New Delhi,Yesterday) cannot be affirmed explicitly.

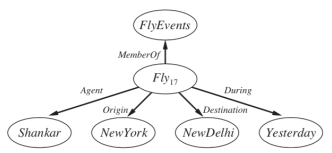
Fig: Fragment of a semantic network showing the representation of the logical assertion Fly(Shankar, New York, New Delhi, Yesterday)

The capacity of semantic networks to represent default values for categories is one of its most essential features.

If you look closely at Figure, you'll find that John only has one leg, despite the fact that he's a person, and all people have two legs.

The default value is said to be overridden by the more particular value. We might alternatively override the default number of legs by adding a One Legged Persons category, which is a subset of Persons that includes John.

If we say that the Legs assertion for Persons includes an exception for John, we can keep the network's semantics purely logical:

∀x x∈ Persons ∧ x _= John ⇒ Legs(x, 2) .

This is semantically appropriate for a fixed network.

Description logics

First-order logic's syntax is intended to make it simple to declare things about objects.

Description logics are notations that make describing the definitions and properties of categories easier.

Subsumption (testing if one category is a subset of another by comparing their definitions) and classification are the two main inference tasks for description logics (checking whether an object belongs to a category)..

The consistency of a category definition—whether the membership criteria are logically satisfiable—is also considered in some systems.

Fig: Syntax of description in sunset of CLASSIC language

A typical description logic is the CLASSIC language (Borgida et al., 1989). Figure depicts the syntax of CLASSIC descriptions.

To say that bachelors are unmarried adult males, for example, we would write

Bachelor = And(Unmarried, Adult ,Male) .

In first-order logic, the equivalent would be

Bachelor (x) ⇔ Unmarried(x) ∧ Adult(x) ∧ Male(x).

Any CLASSIC description can be translated into a first-order equivalent statement, however some CLASSIC descriptions are more clear.

For example, to characterise a group of males who have at least three unemployed sons who are all married to doctors, and at most two daughters who are all professors in physics or math departments, we would use

And(Man, AtLeast(3, Son), AtMost(2, Daughter ),

All(Son, And(Unemployed,Married, All(Spouse, Doctor ))),

All(Daughter , And(Professor , Fills(Department , Physics,Math)))) .

Translating this into first-order logic is left as an exercise.

Negation and disjunction, for example, are generally absent from description logics.

In the Fills and OneOf constructions, CLASSIC only provides for a restricted type of disjunction.

Q18) Write about reasoning with default information?

A18) Circumscription and default logic

When one sees a car parked on the street, for example, one is usually inclined to think it has four wheels despite the fact that only three are visible.

While probability theory can surely lead to the conclusion that the fourth wheel exists with a high probability, most people do not consider the idea that the car does not have four wheels unless new data is presented.

In the absence of any reason to doubt it, it appears that the four-wheel conclusion is reached by default. The conclusion can be retracted if fresh evidence is discovered—for example, if the owner is seen carrying a wheel and the car is jacked up.

Because the collection of beliefs does not develop monotonically over time when new evidence emerges, this type of reasoning is known as non monotonicity.

In order to capture such behaviour, non monotonic logics have been constructed with changed ideas of truth and entailment.

Circumscription and default logic are two such logics that have been extensively investigated.

The closed world assumption can be considered as a more powerful and exact variant of circumscription.

The goal is to define specific predicates that are supposed to be "as false as feasible," that is, false for all objects except those for which they are known to be true.

Let's say we wish to establish the default rule that birds fly.

We'd create a predicate, say Abnormal 1(x), and write it down.

Bird(x) ∧￢Abnormal 1(x) ⇒ Flies(x) .

If we say that Abnormal 1 is to be circumscribed, a circumscriptive reasoner is entitled to assume ￢Abnormal 1(x) unless Abnormal 1(x) is known to be true. This allows the conclusion Flies(Tweety) to be drawn from the premise Bird(Tweety).

Default logic is a formalism that allows for the creation of contingent, non-monotonic conclusions using default principles. The following is an example of a default rule:

Bird(x) : Flies(x)/Flies(x)

If Bird(x) is true and Flies(x) is compatible with the knowledge base, Flies(x) can be concluded by default. In most cases, a default rule looks like this:

P : J1, . . . , Jn/C

P stands for the precondition, C for the conclusion, and Ji for the justifications; if any of them is demonstrated to be untrue, the conclusion cannot be formed.