Unit - 4

Pushdown Automata (PDA)

Q1) Introduce PDA?

A1) It is a way to implement context-free grammar as we design DFA for regular grammar. A DFA can remember a finite amount of information, but a PDA can remember an infinite amount of information.

Basically, a pushdown automaton is -

“Finite state machine” + “a stack”

A pushdown automaton has three components −

●      an input tape,

●      a control unit, and

●      a stack with infinite size.

The stack head scans the top symbol of the stack.

A stack does two operations −

●      Push − a new symbol is added at the top.

●      Pop − the top symbol is read and removed.

A PDA may or may not read an input symbol, but it has to read the top of the stack in

Every transition.

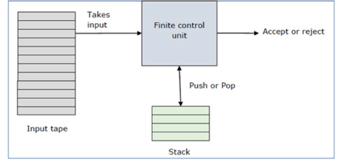
Fig: Basic structure of PDA

A PDA can be formally described as a 7-tuple (Q, ∑, S, δ, q 0 , I, F) −

Where,

●      Q is the finite number of states

●      ∑ is input alphabet

●      S is stack symbols

●      δ is the transition function: Q × (∑ ∪ {ε}) × S × Q × S*)

●      q 0 is the initial state (q 0 ∈ Q)

●      I is the initial stack top symbol (I ∈ S)

●      F is a set of accepting states (F ∈ Q)

The following diagram shows a transition in a PDA from a state q 1 to state q 2, labeled as a, b → c −

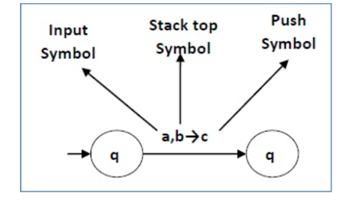
Fig: Example

This means at state q1, if we encounter an input string ‘a’ and the top symbol of the stack is ‘b’, then we pop ‘b’, push ‘c’ on top of the stack and move to state q2 .

Q2) What are the Equivalence of Acceptance by Final State and Empty Stack?

A2) There is a PDA P2 such that L = L (P2) if L = N(P1) for some PDA P1. That is, the language supported by the empty stack PDA will be supported by the end state PDA as well.

Empty stack

If a language L = L (P1) exists for a PDA P1, then L = N (P2) exists for a PDA P2. That is, language supported by the end state PDA is also supported by the empty stack PDA.

The stack of PDAs becomes empty after reading the input string from the initial setup for some PDA.

When a PDA has exhausted its stack after reading the entire string, it accepts a string.

Let P =(Q, ∑, Γ, δ, q0, Z, F) be a PDA. The language acceptable by empty stack can be defined as:

N(PDA) = {w | (q0, w, Z) ⊢* (p, ε, ε), q ∈ Q} 

Example

Construct a PDA that accepts L = {0n 1n | n ≥ 0}

Solution:

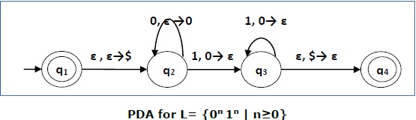
This language accepts L = {ε, 01, 0011, 000111, ............................. }

The number of ‘a' and ‘b' in this example must be the same.

●      We began by inserting the special symbol ‘$' into the empty stack.

●      If we encounter input 0 and top is Null at state q2, we push 0 into the stack. It's possible that this will happen again. We pop this 0 if we meet input 1 and top is 0.

●      If we encounter input 1 at state q3 and the top is 0, we pop this 0. It's possible that this will continue to iterate. We pop the top element if we meet input 1 and top is 0.

●      If the special symbol '$' appears at the top of the stack, it is popped out, and the stack eventually moves to the accepting state q4.

Q3) Explain NPDA?

A3) The non-deterministic pushdown automata is very much similar to NFA. We will

Discuss some CFGs which accept NPDA.

The CFG which accepts deterministic PDA accepts non-deterministic PDAs as well.

Similarly, there are some CFGs which can be accepted only by NPDA and not by

DPDA. Thus NPDA is more powerful than DPDA.

Example:

Design PDA for Palindrome strips.

Solution:

Suppose the language consists of string L = {aba, aa, bb, bab, bbabb, aabaa, ......].

The string can be an odd palindrome or even a palindrome. The logic for constructing PDA is that we will push a symbol onto the stack till half of the string then we will read each symbol and then perform the pop operation. We will compare to see whether the symbol which is popped is similar to the symbol which is read. Whether we reach the end of the input, we expect the stack to be empty.

This PDA is a non-deterministic PDA because finding the mid for the given string and

Reading the string from the left and matching it with the right (reverse) direction leads to non-deterministic moves.

Here is the ID.

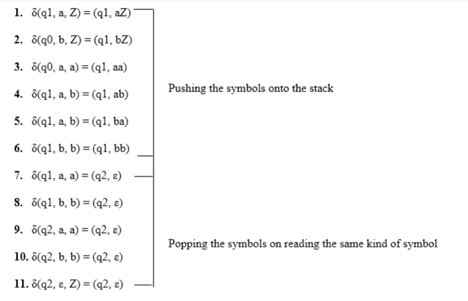
Simulation of abaaba

1. δ(q1, abaaba, Z)            Apply rule 1 

2.  δ(q1, baaba, aZ)          Apply rule 5 

3.  δ(q1, aaba, baZ)          Apply rule 4 

4.  δ(q1, aba, abaZ)          Apply rule 7 

5.  δ(q2, ba, baZ)            Apply rule 8 

6.  δ(q2, a, aZ)              Apply rule 7 

7.  δ(q2, ε, Z)               Apply rule 11 

8.  δ(q2, ε)                  Accept

Q4) Write Algorithm to find PDA corresponding to a given CFG?

A4) Input − A CFG, G = (V, T, P, S)

Output − Equivalent PDA, P = (Q, ∑, S, δ, q0, I, F)

Step1 - Convert the CFG's productions into GNF.

Step2 - There will be only one state q on the PDA.

Step3 - The CFG's start symbol will be the PDA's start sign.

Step4 - The PDA's stack symbols will be all of the CFG's non-terminals, and the PDA's input symbols will be all of the CFG's terminals.

Step5 - For each production in the form A → aX where a is terminal and A, X are a combination of terminal and non-terminals, make a transition δ (q, a, A).

Problem

Construct a PDA using the CFG below.

G = ({S, X}, {a, b}, P, S)

Where are the productions?

S → XS | ε, A → aXb | Ab | ab

Solution

Let's say you have a PDA that's equivalent to that.

P = ({q}, {a, b}, {a, b, X, S}, δ, q, S)

Where δ −

δ(q, ε , S) = {(q, XS), (q, ε )}

δ(q, ε , X) = {(q, aXb), (q, Xb), (q, ab)}

δ(q, a, a) = {(q, ε )}

δ(q, 1, 1) = {(q, ε )}

Q5) Write Algorithm to find CFG corresponding to a given PDA?

A5) Input − A CFG, G = (V, T, P, S)

Output − Equivalent PDA, P = (Q, ∑, S, δ, q0, I, F) such that the non- terminals of the grammar G will be {Xwx | w,x ∈ Q} and the start state will be Aq0,F.

Step1 − For every w, x, y, z ∈ Q, m ∈ S and a, b ∈ ∑, if δ (w, a, ε) contains (y, m) and (z, b, m) contains (x, ε), add the production rule Xwx → a Xyzb in grammar G.

Step2 − For every w, x, y, z ∈ Q, add the production rule Xwx → XwyXyx in grammar G.

Step3 − For w ∈ Q, add the production rule Xww → ε in grammar G.

Q6) Write the Equivalence of PDA and CFG?

A6) The power of a CFG and a PDA is the same: a CFG generates context-free language, while a PDA recognizes context-free language.

We demonstrate how to transform a CFG into a PDA that recognizes the CFG's language and vice versa.

Application: Because of this equivalence, a CFG can be used to specify a programming language, and the equivalent PDA can be used to construct the language's compiler.

Theorem: If a pushdown automaton recognizes a language, it is context-free.

This means that:

1. If a language L is context-free, it is recognized by a PDA ML.

2. If a PDA ML recognizes a language L, there is a CFG GL that generates L.

Lemma: If a language is context-free, it will be recognized by a pushdown automaton.

Proof concept:

1. Let's A pretend to be a CFL. We know from the definition that A has a CFG  G that it generates.

2. We'll demonstrate how to transform G, PDA P into one that accepts strings ພ if G it creates ພ.

3. P will start by figuring out a derivation ພ.

Q7) Write the difference between PDA and CFL?

A7)

Q8) Describe deterministic CFL?

A8) Deterministic context-free languages (DCFL) are a subset of context-free languages in formal language theory. They are the context-free languages that a deterministic pushdown automaton can accept. DCFLs are always unambiguous, which means they accept a clear grammar. Unambiguous CFLs can be non-deterministic, hence DCFLs are a subset of unambiguous CFLs.

Because DCFLs may be parsed in linear time and various constrained variants of DCFGs admit easy practical parsers, they are of tremendous practical interest. As a result, they're commonly employed in computer science.

The deterministic pushdown automaton is strongly connected to the DCFL concept (DPDA). When we make pushdown automatons deterministic, their language power is decreased to the point where they are unable to pick between distinct state-transition options and, as a result, cannot identify any context-free languages. A DCFL is not always generated by unambiguous grammars.

The language of even-length palindromes on the 0 and 1 alphabet, for example, has the unambiguous context-free grammar S → 0S0 | 1S1 | ε. Because an arbitrary string of this language cannot be parsed without first reading all of its letters, a pushdown automaton must experiment with different state transitions to account for the various lengths of a semi-parsed string.

Properties

In polynomial time and O(log2 n) space, a deterministic Turing computer can recognize deterministic context-free languages; as a corollary, DCFL is a subset of the complexity class SC.

The following operations close the set of deterministic context-free languages:

●      complement

●      inverse homomorphism

●      right quotient with a regular language

●      pre: pre(L) is the subset of all strings that have a proper prefix and are also part of display style L.

●      min: min (L) is the subset of all strings in display style L that do not have a suitable prefix.

●      max: max (L) is the subset of all strings in display style L that are not the prefix of a longer string.

Importance

This class of languages has a lot of practical value in computer science since they can be parsed significantly faster than non-deterministic context-free languages. A deterministic pushdown automaton's program complexity and execution time are significantly lower than those of a nondeterministic one. When a nondeterministic step happens in the naive implementation, the latter must make copies of the stack.

Valiant's algorithm is the most well-known algorithm for testing membership in any context-free language, and it takes O(n2.378) time, where n is the length of the string. An LR(k) parser, on the other hand, can accept deterministic context-free languages in O(n) time. This is very important for computer language translation because many computer languages belong to this class of languages.

Q9) Convert the following grammar to a PDA that accepts the same language. S → 0S1 | A and A → 1A0 | S | ε 

A9) The CFG can be first simplified by eliminating unit productions:

1. S → 0S1 | 1S0 | ε 

Now we will convert this CFG to GNF:

1. S → 0SX | 1SY | ε 
2. X → 1 
3. Y → 0 

The PDA can be:

R1: δ(q, ε, S) = {(q, 0SX) | (q, 1SY) | (q, ε)}

R2: δ(q, ε, X) = {(q, 1)}

R3: δ(q, ε, Y) = {(q, 0)}

R4: δ(q, 0, 0) = {(q, ε)}

R5: δ(q, 1, 1) = {(q, ε)}

Q10) Construct PDA for the given CFG, and test whether 0104 is acceptable by this PDA. S → 0BB   and B → 0S | 1S | 0 

A10) The PDA can be given as:

1. A = {(q), (0, 1), (S, B, 0, 1), δ, q, S, ?} 

The production rule δ can be:

R1: δ(q, ε, S) = {(q, 0BB)}

R2: δ(q, ε, B) = {(q, 0S) | (q, 1S) | (q, 0)}

R3: δ(q, 0, 0) = {(q, ε)}

R4: δ(q, 1, 1) = {(q, ε)}

Testing 0104 i.e. 010000 against PDA:

δ(q, 010000, S) ⊢ δ(q, 010000, 0BB) 

⊢ δ(q, 10000, BB)              R1 

⊢ δ(q, 10000,1SB)              R3   

⊢ δ(q, 0000, SB)               R2       

⊢ δ(q, 0000, 0BBB)             R1    

⊢ δ(q, 000, BBB)               R3       

⊢ δ(q, 000, 0BB)               R2     

⊢ δ(q, 00, BB)                 R3    

⊢ δ(q, 00, 0B)                 R2   

⊢ δ(q, 0, B)                   R3   

⊢ δ(q, 0, 0)                   R2 

⊢ δ(q, ε)                      R3   

ACCEPT 

Thus 0104 is accepted by the PDA.

Q11) Draw a PDA for the CFG given below:

1. S → aSb 
2. S → a | b | ε

A11) The PDA can be given as:

1. P = {(q), (a, b), (S, a, b, z0), δ, q, z0, q} 

The mapping function δ will be:

R1: δ(q, ε, S) = {(q, aSb)}

R2: δ(q, ε, S) = {(q, a) | (q, b) | (q, ε)}

R3: δ(q, a, a) = {(q, ε)}

R4: δ(q, b, b) = {(q, ε)}

R5: δ(q, ε, z0) = {(q, ε)}

Simulation: Consider the string aaabb

1. δ(q, εaaabb, S) ⊢ δ(q, aaabb, aSb)             R3 
2. ⊢ δ(q, εaabb, Sb)              R1                                
3. ⊢ δ(q, aabb, aSbb)             R3 
4. ⊢ δ(q, εabb, Sbb)              R2 
5. ⊢ δ(q, abb, abb)               R3 
6. ⊢ δ(q, bb, bb)                 R4 
7. ⊢ δ(q, b, b)                   R4 
8. ⊢ δ(q, ε, z0)                  R5 
9. ⊢ δ(q, ε) 
10. ACCEPT 

Q12) Design a PDA for accepting a language {0n1m0n | m, n>=1}?

A12) In this PDA, n number of 0's are followed by any number of 1's followed n number of 0's. Hence the logic for design of such PDA will be as follows:

Push all 0's onto the stack on encountering first 0's. Then if we read 1, just do nothing. Then read 0, and on each read of 0, pop one 0 from the stack.

For instance:

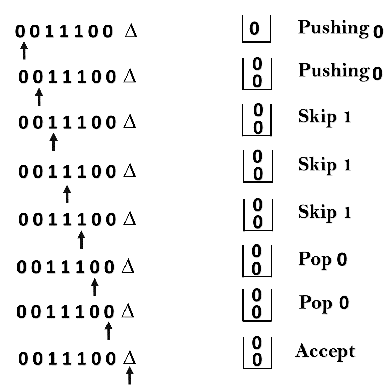
This scenario can be written in the ID form as:

1. δ(q0, 0, Z) = δ(q0, 0Z) 
2. δ(q0, 0, 0) = δ(q0, 00) 
3. δ(q0, 1, 0) = δ(q1, 0) 
4. δ(q0, 1, 0) = δ(q1, 0) 
5. δ(q1, 0, 0) = δ(q1, ε) 
6. δ(q0, ε, Z) = δ(q2, Z)      (ACCEPT state) 

Now we will simulate this PDA for the input string "0011100".

1. δ(q0, 0011100, Z) ⊢ δ(q0, 011100, 0Z) 
2. ⊢ δ(q0, 11100, 00Z) 
3. ⊢ δ(q0, 1100, 00Z) 
4. ⊢ δ(q1, 100, 00Z) 
5. ⊢ δ(q1, 00, 00Z) 
6. ⊢ δ(q1, 0, 0Z) 
7. ⊢ δ(q1, ε, Z) 
8. ⊢ δ(q2, Z) 
9. ACCEPT 

Q13) Design a PDA for accepting a language {anb2n | n>=1}?

A13) In this language, n number of a's should be followed by 2n number of b's. Hence, we will apply a very simple logic, and that is if we read single 'a', we will push two a's onto the stack. As soon as we read 'b' then for every single 'b' only one 'a' should get popped from the stack.

The ID can be constructed as follows:

1. δ(q0, a, Z) = (q0, aaZ) 
2. δ(q0, a, a) = (q0, aaa) 

Now when we read b, we will change the state from q0 to q1 and start popping corresponding 'a'. Hence,

1. δ(q0, b, a) = (q1, ε) 

Thus this process of popping 'b' will be repeated unless all the symbols are read. Note that popping action occurs in state q1 only.

1. δ(q1, b, a) = (q1, ε) 

After reading all b's, all the corresponding a's should get popped. Hence when we read ε as input symbol then there should be nothing in the stack. Hence the move will be:

1. δ(q1, ε, Z) = (q2, ε) 

Where

PDA = ({q0, q1, q2}, {a, b}, {a, Z}, δ, q0, Z, {q2})

We can summarize the ID as:

1. δ(q0, a, Z) = (q0, aaZ) 
2. δ(q0, a, a) = (q0, aaa) 
3. δ(q0, b, a) = (q1, ε) 
4. δ(q1, b, a) = (q1, ε) 
5. δ(q1, ε, Z) = (q2, ε) 

Now we will simulate this PDA for the input string "aaabbbbbb".

δ(q0, aaabbbbbb, Z) ⊢ δ(q0, aabbbbbb, aaZ) 

⊢ δ(q0, abbbbbb, aaaaZ) 

⊢ δ(q0, bbbbbb, aaaaaaZ) 

⊢ δ(q1, bbbbb, aaaaaZ) 

⊢ δ(q1, bbbb, aaaaZ) 

⊢ δ(q1, bbb, aaaZ) 

⊢ δ(q1, bb, aaZ) 

⊢ δ(q1, b, aZ) 

⊢ δ(q1, ε, Z) 

⊢ δ(q2, ε)       

ACCEPT