Unit - 1

Basics of Control System

Q1) Find SFG for the block diagram below?

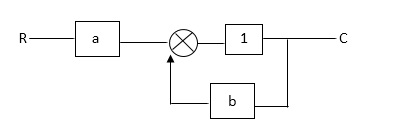
Fig 1 Block Diagram

A1)

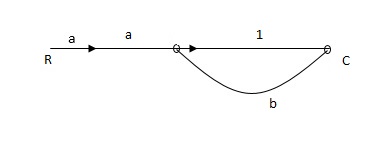
Fig 2: Required SFG

Ra+cb =c

c/R= a/1-b

Q2) The SFG shown has forward path and singles isolated loop determine overall transmittance relating X3 and X1­?

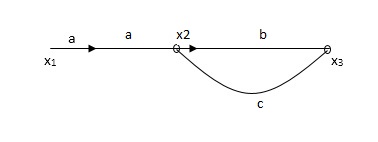
Fig 3 SFG

A2)

X1- I/p node

X2-Intenmediale node

X3- o/p node

Ab- forward path (p)

Bc- 1 loop (L)

At node XQ:

X2 = x1a + x3c [Add i/p signals at  node]

At node x3:

x2b =x3

(x1a+x3c) b = x3

X1ab = x3 (1-bc)

X1 = x3 (1-bc)/ab

Ab/(1-bc) = x3/x1

T= p/1-L

Q3) Find the Transfer function for the SFG given below?

Fig 4 SFG

A3)

X1:- I/p node    x2, x3,x4,x5,Qnlexmedili node

X0:- o/p node  abdeg:- forward path

Bc, ef :- Loop [isolated] 

x2 = ax1+c x3

x3= bx2

x4 = d x3+f x5

x5 = e x4

x6= g x5

x6 = g(e x4) = ge [dx3+ e f x5]

xb = ge [d (bx2) + f (e x4)]

xb = ge [ db (ax1+cx3) + fe (dx3+ fx5)]

xb = ge [db (ax1+cb (ax1+x3) +fe[cdbx2]+

f( e [db (ax1+ cx3)

x2 = ax1 + cb (x2)  x4 = d bx2 + f exq

x2 = ax1 + cbx2          = db (d4) + fe/1-cb

x2 = ax1/(1-cb)   xy = db x2 + f x6/g

xy = db [ax1]/1-cb + f xb/g

x5 = c db ( ax1)/1-cb + efxb/g

xb = gx5

= gedb (ax1)/1-cb + g efxb/g

Xb = gx5

Gedb (ax1)/1-cb + g efxb/g

(1- gef/g) xb = gedb ax1/1-ab

Xb/x1 = gedb a/ (1- ef – bc + beef

Xb/x1 = p/ 1- (L1+L2) + L1 L2 for isolated loops

Q4) Reduce given B.D to canonical (simple form) and hence obtain the equivalent Tf = c(s)/ R(S)?

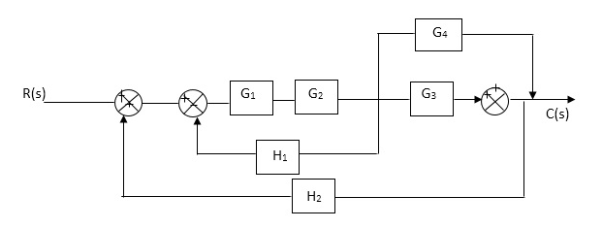
Fig 5 Block Diagram

A4)

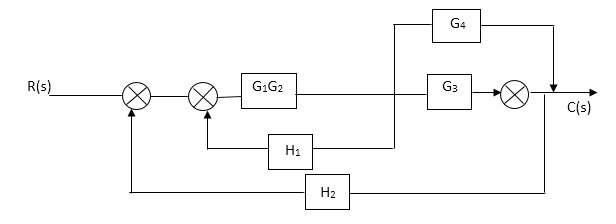
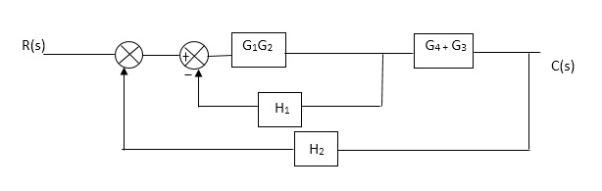
Fig 6 Reduced Block Diagram

C(S)/R(S) = (G1G2) (G3+G4)/1+G1G2H1)/1-G1,G2(G3+G4) H2/1+G1G2H1

= G1G2(G3+G4)/1+G1G2H1-G1G2H2(G3+G4)

=G1G2(G3+G4)/1+(H1-H2)(G1G2) (G3+G4)

C(s)/R(S) = G1G2(G3+G4)/1+(H1-H2(G3+G4)) G1 G2

Q5) Reduce the Block diagram

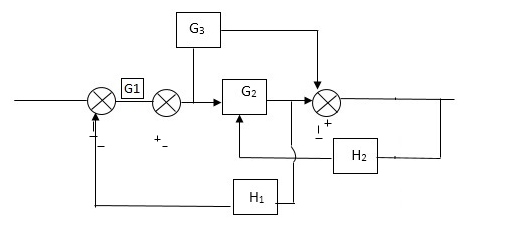
Fig 7 Block Diagram

A5)

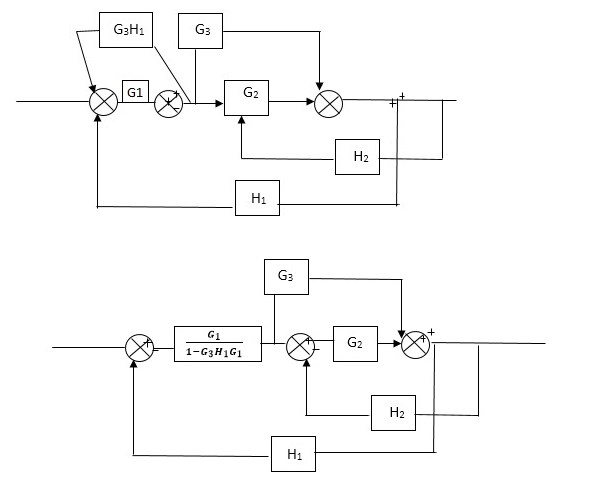
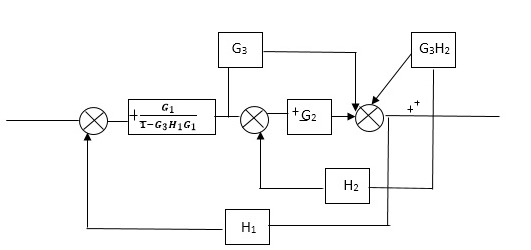
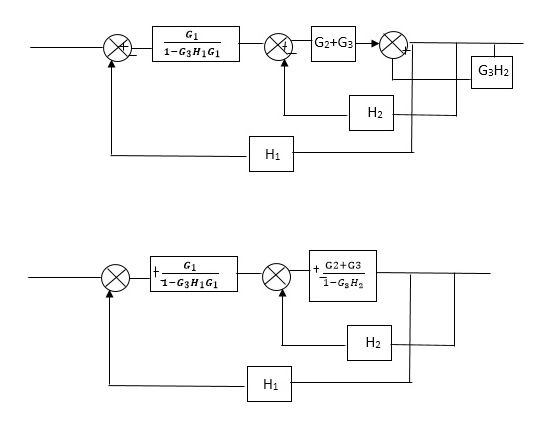
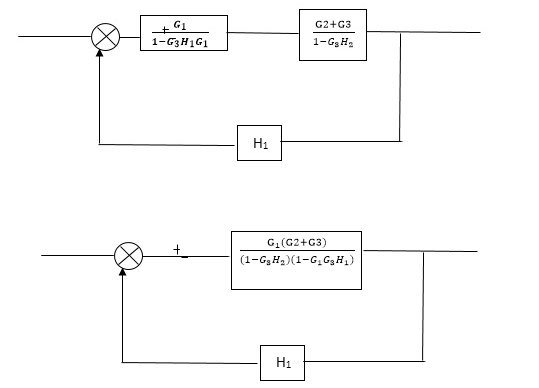
Fig 8 Final Reduced Block Diagram

C(s)/R(s)=  G1(G3+G2)/(1-G1G3X1) (1-G2X2) H1

= G(G3+G2)/(1-G3G1H1) (1-G2H2) + G1H1(G3+G2)

= G1(G3+G2)/1-63G1H1-G2H2+G1H1(G3+G2H1

=G1(G3+G2)/1-G3H2+G1G2H1(1+G3H2)

Q6) Reduce using Masons gain formula

Fig 9 Block Diagram

A6)
 

Fig 10 SFG for Fig 8

P1= G1 p2 =G2 Delta1 =1

L1= -G1 H1

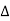= 1-(-G1H1)

= 1+G1H1

T= G1+G2/1+G1H1

Q7) Determine overall gain reliably x5 and x1 Draw SFG

X2 = ax1+ f x2

X3= bx2 +exy

X4 = cx3+hx5

X5 =dx4 + gx2

A7)

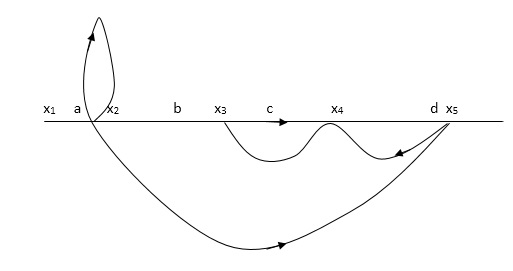
Fig 11 SFG

P1 = abcd       p2 = ag

L1 = f   L2 = ce, L3= dh

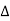1 = 1

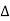2= 1-ce

= 1-[L2+L2+L3] + [L1 L2 +L1 L3]

= 1-[f+ le = dh] + [fce +fdh]

T= abcd+ ag (1-ce)/1-[ftce + dh ] + (fce + fdh)

Q8) For the given electrical system below draw the analogous system find V0(s)/V1(s)

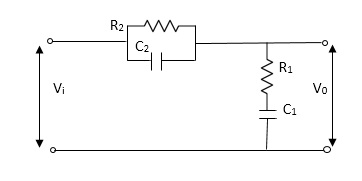
Fig 12 Electrical Circuit

A8)

Let     Z1   = R2 11 1/c2

=R2*1/c2s/R2+1/c2s

Z1= R2/1+R2c2s

Let     Z2 = R1+1/c1s

Z2= 1+R1c1s/c1s

V0(s)/vi(s) = z2/z1+z2

=1+R1c1s/c1s/R2/1+R2c2s+1+R1c1s/c1s

V0(s)/v0(s) =(c1+R1c1s) (1+R2c2s)/R2c1s+1+sR1c1s2R1R2c1c2

Q9) Difference between open and closed loop system?

A9)

Q10) Explain Mason’s gain formula?

A10)

T=

The overall transmittance Coverall gain can be determined by Masks formula.

Explanation:

Pkforward path transmittance of k+n path from a specified i/p node to n  o/p nods

While calculating ipnode  to n  o/p nods.

While calculating ip no node should be encountered (used) more than ones.

it is the graphics determined which involves of transmittances and multiple increases b/w non touching loops.

= 1- [sum of all individual loop transmitting]

+[ sum of loop transmittance product of all possible non- touching loops]

-[sum of loop transmittance  of all possible triples of non- touching loops]

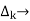path factor associated with concered path & involves all a in the graphic which are isolated from forward path under consideration.

The path factor 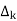 for kthis equal to graph determinant of SFG which effect after erasing the kth path from the graph

Q11) List advantages of block diagram reduction technique?

A11)

1. Very simple to Construct the Block diagram of complicated electrical & mechanical sys.
2. The function of individual element can be visualized form block diagram
3. Individual as well as overall performance of the system can be studied by the if shown in Block diag.
4. Overall CLTf can be easily calculated by Block diagram reduction rules.