Unit 1

Network Theorems

Q1) Using Superposition theorem determine the voltage drop and current across the resistor 3.3K as shown in figure below

A1)

Step 1:

Remove 8V power supply from the original circuit such that the new circuit becomes as the following and measure the voltage across resistor.

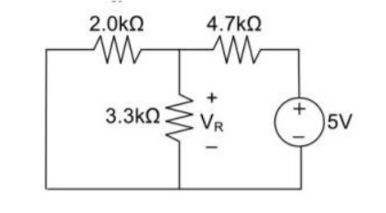
Here 3.3 K and 2K are in parallel therefore the resultant resistance will be 1.245K

Using voltage divider rule across 1.245K will be

V1 =[1.245/(1.245+4.7)] * 5 = 1.047V

Step 2:

Remove the 5V power supply from the original circuit such that the new circuit becomes the following and then measure the voltage across resistor.

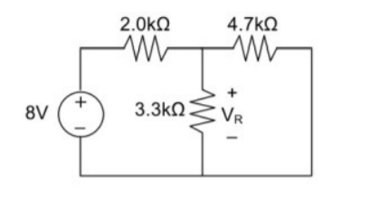
Here 3.3K and 4.7K are in parallel therefore the resultant resistance will be 1.938K. Using voltage divider rule voltage across 1.938K will be

V2 =[1.938(1.938+2)] *8 = 3.9377V

Therefore, voltage drop across 3.3K resistor is V1+V2 = 1.047 + 3.9377 = 4.9847V

Q2) Explain Thevenin’s theorem?

A2)

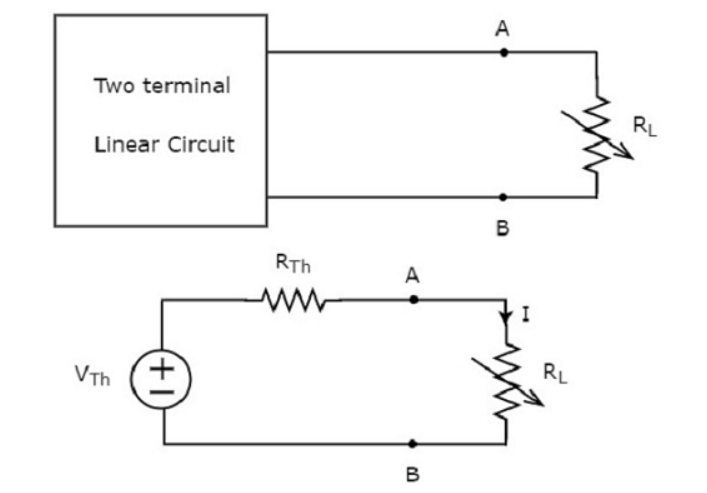
Thevenin’s Theorem states that “Any linear circuit containing several voltages and resistances can be replaced by just one single voltage in series with a single resistance connected across the load”.

To simplify any electrical circuit, to an equivalent two-terminal circuit with just a single constant voltage source in series with a resistance (or impedance) connected to a load as shown below.

Q3) For the circuit as shown in figure find the current through RL = R2 = 1Ω resistor (Ia-b) branch using Thevenin’s theorem. Find the voltage across the current source.

A3)

Step 1: Disconnect the load resistance and reconnect the circuit.

Step 2: Apply any method to calculate Vth

At node C

2 + I1 + I2 =0

2 + (3 -Vc)/3 + (0-Vc/6) -- Vc = 6V

The currents I1 and I2 are computed by the following expressions:

I1 = Va -Vc/3 = 3-6/3 = -1A (I1 is flowing from c to a)

I2 = 0 – Vc/6  = -6/6 = -1A (I2 is flowing from c to a)

Step-3:

Redraw the circuit indicating the direction of currents in different branches. One can find the Thevenin’s voltage VTh using KVL around the closed path ‘gabg’

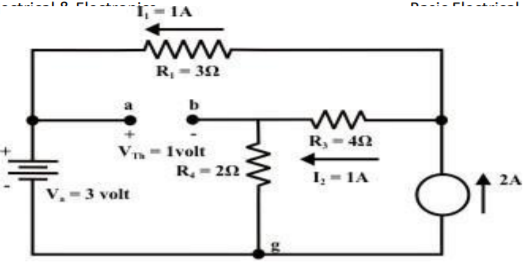
VTh = Vag − Vbg = 3 − 2 =1volt

Step 4:

Replace all sources by their internal resistances. In this problem, voltage source has an internal resistance zero (0) (ideal voltage source) and it is short-circuited with a wire.

On the other hand, the current source has an infinite internal resistance (ideal current source) and it is open-circuited (just remove the current source).

Thevenin’s resistance RTh of the fixed part of the circuit can be computed by looking at the load terminals ‘a’- ‘b’

RTh = ( R1 + R3 ) & R4 = ( 3 + 4 )&2 = 1.555Ω

Step-5: Place RTh in series with VTh to form the Thevenin’s equivalent circuit. Reconnect the original load resistance RL = R2 = 1 Ω to the Thevenin’s equivalent circuit .

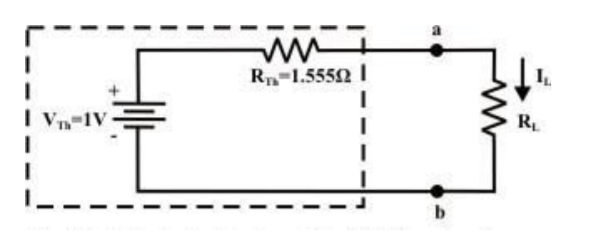
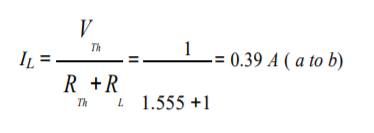
Step-6: The circuit is redrawn to indicate different branch currents. Referring to one can calculate the voltage Vbg and voltage across the current source (Vcg ) using the following equations.

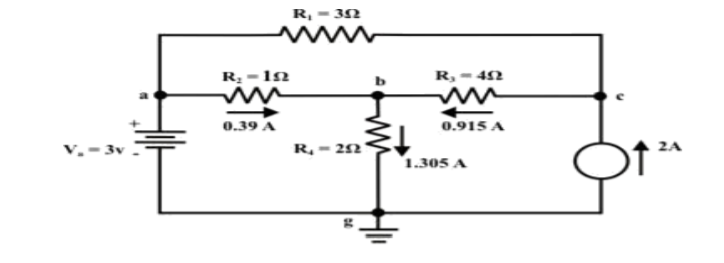
Vbg = Vag − Vab = 3 − 1 × 0.39 =2.61 volt.

Ibg = 2.61 2 = 1.305 A;

Icb = 1.305 − 0.39 = 0.915 A

Vcg = 4 × 0.915 + 2 ×1.305 =6.27 volt.

Q4) Explain Norton’s theorem?

A4)

Norton’s Theorem states that “Any linear circuit containing several energy sources and resistances can be replaced by a single Constant Current generator in parallel with a Single Resistor”.

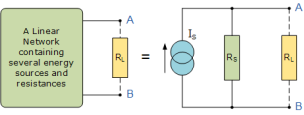
Q5) Find RN, IN, the current flowing through and load Voltage across the load resistor in fig (1) by using Norton’s Theorem.

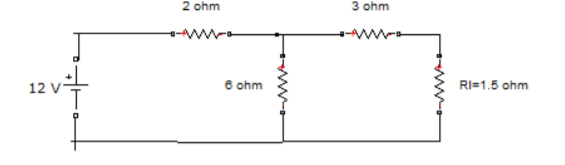
A5)

Step 1:

Short the 1.5 Ω load resistor.

Step 2:

Norton current.

Short AB terminals to obtain IN . The total resistance of the circuit is

2Ω + (6Ω || 3Ω)

RT = 4 Ω

IT = V / RT = 12/ 4 = 3 A

IN = 3 A x [ 6Ω / 3 + 6 )] = 2A

IN = 2A

Step 3:

Open current sources, Short Voltage sources and Open Load resistor.

Step 4:

Calculate Norton Resistance (RN)

Reduce 12V dc source. 3Ω resistor is in series with combination of 6Ω and 2Ω resistor

3Ω + (6Ω||2Ω)

3Ω + 1.5 Ω = 4.5 Ω; RN = 4.5 Ω

Step 5:

Connect RN in parallel with current source IN and the load resistor.

Step 6:

The load current through Load resistor

IL = IN x [ RN /(RN + RL)

=2 A x ( 4.5 / 4.5 + 1.5 K) = 1.5 A

IL = 1.5 A

The voltage across load resistor

VL = IL x RL

      = 1.5 x 1.5

VL = 2.25 V

Q6) Explain maximum power transfer theorem?

A6)

Maximum power transfer theorem states that AC voltage source will deliver maximum power to the variable complex load only when the load impedance is equal to the complex conjugate of source impedance.

Proof:

Replace any two terminal linear network or circuit to the left side of variable load resistor having resistance of RL ohms with a Thevenin’s equivalent circuit. We know that Thevenin’s equivalent circuit resembles a practical voltage source.

The amount of power dissipated across the load resistor is

                                     PL = I 2 R L      ----------------------(1)

Substitute I = Vth / Rth + RL

PL = Vth / (Rth + RL ) 2 RL

PL = Vth 2 { RL / (RTH + RL) 2 ------------------------------(2)

Condition for Maximum Power Transfer

For maximum or minimum, first derivative will be zero. So, differentiate Equation 1 with respect to RL and make it equal to zero.

DPL / d RL = V Th 2 { (Rth + RL) 2 x 1 -RL x 2(Rth + RL) / (Rth + RL) 4 } =0

(Rth + RL) 2 – 2RL (Rth + RL) = 0

(Rth + RL) (Rth + RL – 2 RL) = 0

Rth - RL = 0

Rth = RL  or RL  = Rth

Therefore, the condition for maximum power dissipation across the load is RL=RTh. That means, if the value of load resistance is equal to the value of source resistance that is Thevenin’s resistance, then the power dissipated across the load will be of maximum value.

Substitute RL = Rth and PL = PL,max

PL,max = V th 2 { Rth / (Rth + Rth ) 2 }

= V th 2 ( Rth / 4 Rth 2 )

= V th 2 / 4 Rth

PL,max = V th 2 / 4 RL                                                     [RL = Rth]

Efficiency of Maximum power transfer

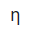= PL,max/ Ps

PL,max = maximum amount of power transferred to the load

Ps = amount of power generated by the source.

The amount of power generated by the source is

Ps = I2 Rth + I2 RL

Ps = 2 I2 Rth ; since RL = Rth

Substitute I = Vth / 2 Rth

Ps = 2(Vth / 2Rth) 2 Rth

Ps = 2(Vth / 4Rth) 2 Rth

Ps = Vth 2 / 2 Rth

Substituting with PL max and Ps

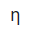= (Vth 2 / 4 Rth) / (Vth 2 / 2 Rth)

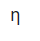max =  ½

Q7) Find the maximum power that can be delivered to the load resistor RL of the circuit shown in the following figure.

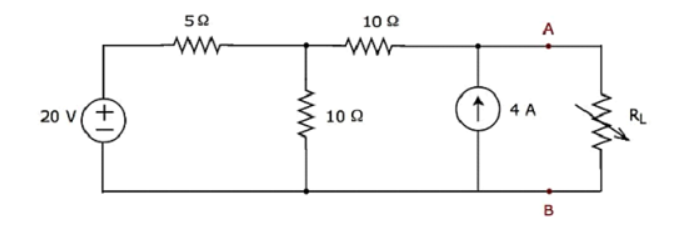
A7)

Step 1 – Using Thevenin’s circuit we get

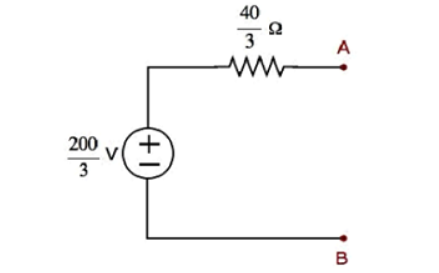
Thevenin’s voltage Vth = 200/3 and Thevenin’s resistance Rth = 40/3

Step 2 – Replace the left side of terminals A & B of the given circuit with the above Thevenin’s equivalent circuit. The resultant circuit diagram will be

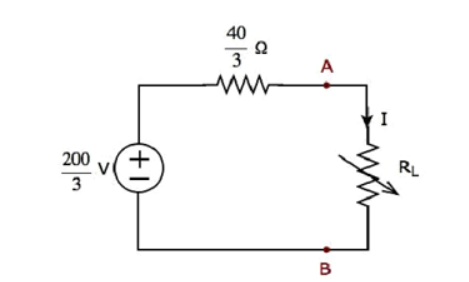
Step 3 − We can find the maximum power that will be delivered to the load resistor, RL by using the following formula.

                                    P L,max = Vth 2 / 4 Rth

  Substitute VTh=200/3 and RTh=40/3Ω

P L,max = (200/3) 2 / 4 (40/3)

Therefore, the maximum power that will be delivered to the load resistor RL of the given circuit is 250/3 .

Q8) Explain reciprocity theorem?

A8)

The reciprocity theorem states that in a linear passive bilateral network by changing the voltage source from branch 1 to branch2, the current I in the branch 2 appears in branch 1.

The resistances R1, R2 and R3 is connected in the circuit diagram. It is clearly shown the voltage and current sources are interchanged for solving the network.

Step 1 – Firstly, select the branches between which reciprocity is established.

Step 2 – The current in the branch is obtained using any conventional network analysis method.

Step 3 – The voltage source is interchanged between the branch which is selected.

Step 4 – The current in the branch where the voltage source was existing earlier is calculated.

Step 5 – Hence it is seen that the current obtained in the previous connection, that is  step 2 and the current which is calculated when the source is interchanged, that is step 4 are identical to each other.

Q9) Verify the reciprocity theorem for the given network.

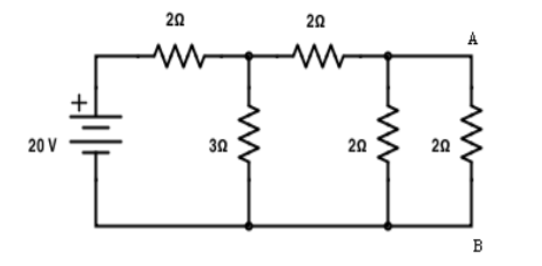
A9)

Find the current in branch AB

RT = 2+[3||(2 + 2 || 2)

RT = 3.5 Ω

IT = V / RT = 20/3.5 = 5.71 A

Apply current division technique for the circuit to find the current through branch AB

= 5.71 x 3 / 6 = 2.855 A

Current in branch AB = 2.855 x 2/4 = 1.43A

Interchanging the source to branch AB

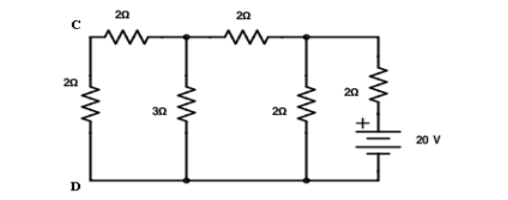
Total resistance RT = 3.23Ω IT = 20/3.23 = 6.19A

Apply current division technique for the circuit to find current through branch CD = 6.19 x 2/5.2 = 2.38A

Current in branch CD = 2.38 x 3/5 = 1.43A

Hence reciprocity theorem verified.

Verify the reciprocity theorem for the given circuit:

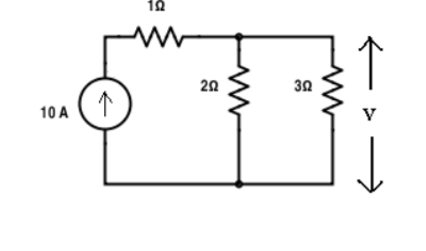
Apply current division technique for the circuit to find current through branch 3Ω

= 10 x 2 / 5 = 4 A.

Voltage across 3Ω = 4 x 3 = 12 V

Replace the current source and find the open circuit voltage.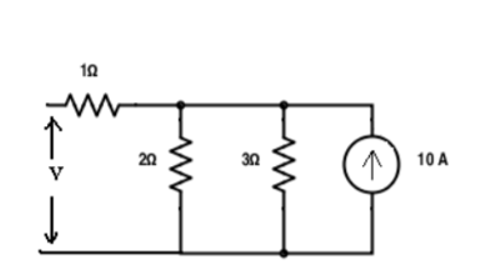                         

Apply current division technique and find the current through 2 Ω resistor.

= 10 x 3 / 5 = 6

Voltage across 2Ω resistor = voltage across AB = 6 x 2 = 12 V

Q10) Explain compensation theorem?

A10)

This theorem states that in a linear time-invariant network when the resistance R  of an uncoupled branch carrying current I is changed by ∆R then the currents would change which can be obtained by assuming that an ideal voltage source VC has been connected such that Vc = I ∆R in series with (R + ∆R) when all other sources in the network are replaced by their internal resistances.

Let us assume a load RL be connected to a DC source network whose Thevenin’s equivalent gives V0 as the Thevenin’s voltage and RTH as the Thevenin’s resistance as shown in the figure below:

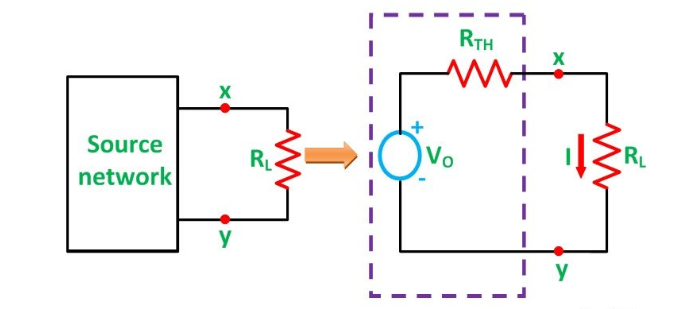
Here,

I = Vo / Rth + RL ------------------------------------(1)

Let the load resistance RL be changed to (RL + ΔRL).

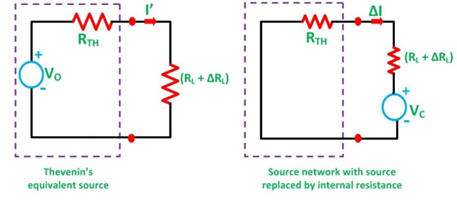
Here,

                          I ‘ = Vo/ Rth + (RL + ∆ RL) ------------------------(2)

The change of current is ∆I

Therefore,

             ∆I = I’ – I -------------------------------------(3)

Putting the value of I’ and I from the equation (1) and (2) in equation(3) we get

∆I = Vo / Rth + (RL + ∆ RL)   - Vo / Rth + RL --------------------------(4)

∆I = Vo {Rth +RL – (Rth + RL + ∆ RL )} / (Rth + RL + ∆RL ) (Rth + RL)

∆I = - [ Vo/Rth + RL] ∆ RL / Rth + RL + ∆ RL -------------------------------------------------(5)

Now, putting the value of I from the equation (1) in equation (5), we will get the following equation:

∆I = - I ∆ RL / Rth + RL + ∆ RL ------------------------------------------------(6)

VC = I ΔRL and is known as compensating voltage.

∆I = -Vc / Rth + RL + ∆ RL

Hence, Compensation theorem states that the change of branch resistance, results a change in branch currents and the change is equivalent to an ideal compensating voltage source in series with the branch opposing the original current, where all other sources in the network being replaced by their internal resistances.

Q11) Explain dependent current and source voltage?

A11)

Dependent current source

Dependent current source changes its available current depending upon the voltage across, or the current through, and some other element connected to the circuit.

That is the output of a dependent current source is controlled by another voltage or current.

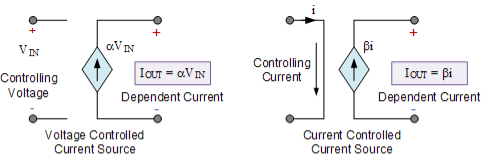
A current source that depends on a voltage input is generally referred to as a Voltage Controlled Current Source or VCCS. A current source that depends on a current input is generally referred as a Current Controlled Current Source or CCCS.

Dependent Current Source Symbols

A voltage source that depends on a voltage input is generally referred to as a Voltage Controlled Voltage Source or VCVS. A voltage source that depends on a current input is referred as a Current Controlled Voltage Source or CCVS.

Ideal dependent sources are commonly used in the analysing the input/output characteristics or the gain of circuit elements such as operational amplifiers, transistors and integrated circuits. 

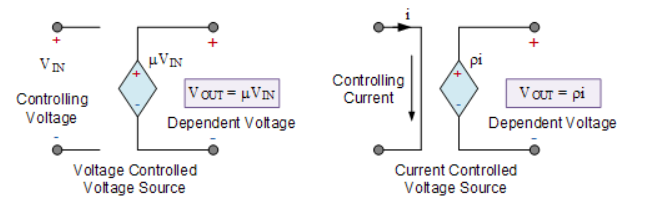
An ideal dependent voltage-controlled current source, VCCS, maintains an output current, IOUT that is proportional to the controlling input voltage, VIN.

That is the output current “depends” on the value of input voltage making it a dependent current source. Then, the VCCS output current is defined by

IOUT = α VIN.

This multiplying constant α has the SI units of mhos, ℧  because α = IOUT/VIN, and its units will therefore be amperes/volt.

Q12) Explain nodal analysis and mesh analysis?

A12)

Nodal analysis

In the nodal method we are finding the node voltages with the following steps:

1. Select a reference node. Assign all the rest nodes voltages , with respect to reference node.
2. Use Kirchhoff’s and Ohm’s Laws to each non-reference node and branch currents.
3. Resolve the system of equations and obtain node voltages.

Consider the following circuit.

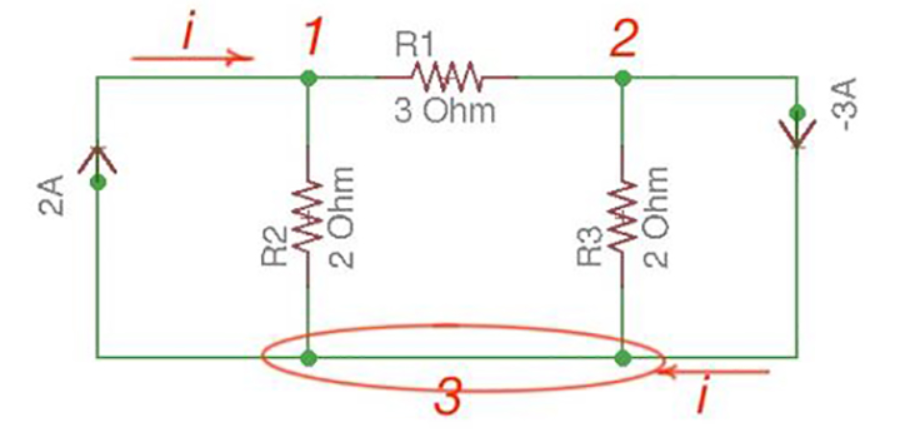
Let us consider a reference node – 3.

In a real circuit a reference node is ground is assumed to have potential.

By the Kirchhoff’s Law having the following current relation:

I1 = i1 + i2

I2 = i2 -i3

Let us represent currents like ratio of voltage and resistance by the Ohm’s Law:

i 1 = v1 /R1 ; i 2 = v1 -v2 /R2 ; i3 = v2/R3;

Or

i 1= v1 * G1 ; i2 =(v1 -v2)*G2 ; i3 =v2 * G3

i1 = v1 * G1 + (v1-v2) * G2 ;

i2 = (v1-v2) * G2 – v2 * G3

i1= v1 * (G1 +G2) – v2 * G2

i2 = v1 *G2 – v2 *(G3 +G2)

Or

And we achieve the following matrix equation, which can be resolved by the Cramer’s rule:

[ G1 + G2 -G3 -G3 ] [v1] = [I1]

[     G2                -G2][v2] =[I2]

Consider the following figure :

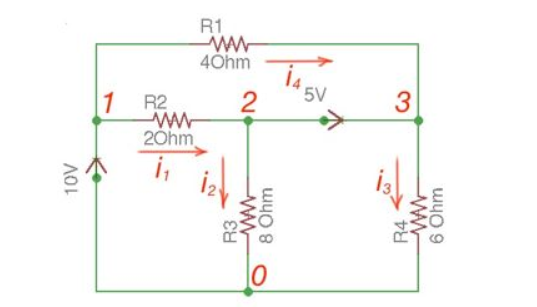
There are two possibilities that exist:

1. If the voltage source is between reference node and non-reference node, the non-reference voltage is considered equal to the voltage source.
2. If the voltage source is between two non-reference nodes, these two nodes are generalised nodes. To determine its voltage Kirchhoff’s Laws must be applied.

Applying Kirchhoff’s Law we achieve the following equations:

i  1 + i4 = i2 + i3

-v2 +5+v3 =0

v 1 =10

By Ohm’s Law

These equations will help determine node voltages.

Mesh Analysis

Mesh analysis is applicable to the networks which are planar. Planar network is a network where branches are not passing over or under each other.

Nodal method uses Kirchhoff’s currents Law to consider nodal voltages, and Mesh method uses Kirchhoff’s voltages Law to consider mesh currents. Mesh  is a loop, which does not contain any other loops.

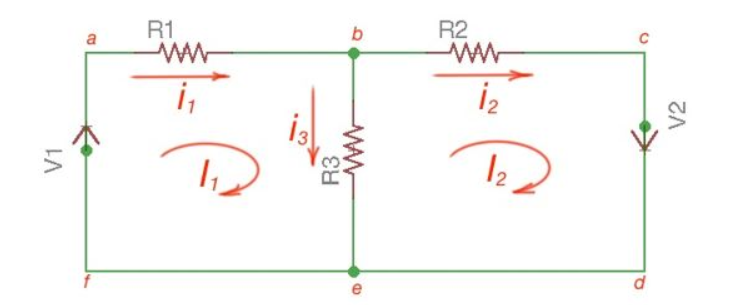
There are only two meshes in abefa and bcdeb, abcdefa is not a mesh but a loop However, for Mesh method only meshes are in use.

Mesh analysis steps are the following:

1. Assign mesh currents to all the meshes in a circuit.
2. Apply Kirchhoff’s voltage Law to each mesh. Apply Ohm’s Law to determine voltages with mesh currents.
3. To resolve simultaneously all the equations to consider mesh currents.

The following equations correspond to the Kirchhoff’s Voltage Laws for the meshes:

V1 = i1 *(R1+R3) – i2 *R3

-V2 = -i1 *R3 + i2 * (R3 +R2);

[ R1 +R3    -R3       [i1]= [V1]

-R3           R2+R3] [i2] = [V2]

Using Cramer’s formula for resolving the matrix equations above we can find mesh currents.

I1 =i 1 I2 = i2  I1 -I2 =i3

Q13) Find the current flowing through 20 Ω resistor of the following circuit using Nodal analysis.

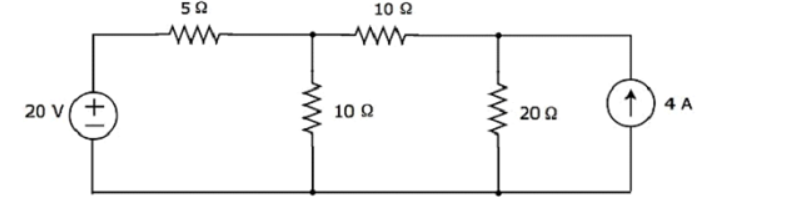
A13)

Step 1 − There are three principle nodes in the above circuit. Those are labelled as 1, 2, and 3 in the following figure. In the above figure, consider node 3 as reference node (Ground).

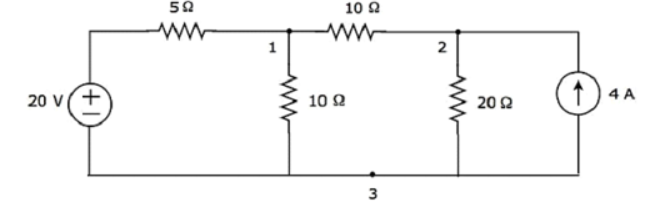
Step 2 − The node voltages, V1 and V2, are labelled in the following figure.

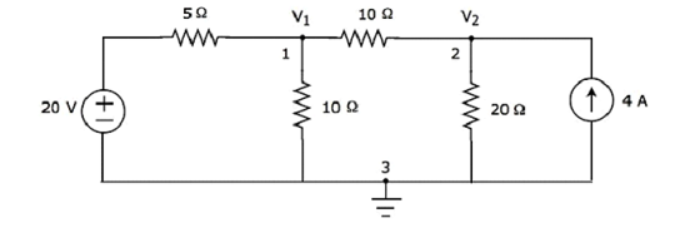
Step 3 – There are two nodal equations, since there are two principal nodes, 1 and 2, other than Ground.

The nodal equation at node 1 is

V1 -20/5 + V1/10 + V1-V2/10 =0

2V1 -40 +V1+V1-V2/10 =0

4V1 -40-V2 =0 --- V2 = 4V1-40 -------(1)

The nodal equation at node 2 is

-4 +V2/20 + V2-V1/10 =0

-80 + V2 + 2 V2 – 2V2/ 20 =0

= 3V2 -2V1 =80 --------------(2)

Step 4 − Finding node voltages, V1 and V2 by solving Equation 1 and Equation 2.

Substitute Equation 1 in Equation 2.

3(4V1−40)−2V1=80

⇒12V1−120−2V1=80

⇒10V1=200

⇒V1=20V

Substitute V1 = 20 V in Equation1.

V2=4(20)−40

⇒V2=40V

So, we got the node voltages V1 and V2 as 20 V and 40 V respectively.

Step 5 − The voltage across 20 Ω resistor is nothing but the node voltage V2 and it is equal to 40 V. Now, we can find the current flowing through 20 Ω resistor by using Ohm’s law.

                                 I 20Ω = V2/R

Substitute the values of V2 and R

I 20 Ω = 40/20

                              I 20Ω = 2A

Therefore, the current flowing through the 20Ω resistor is 2A.