UNIT 4
KINETICS OF RIGID BODY
Q1) Difference between Perpendicular Axis Theorem and Parallel Axis Theorem
A1)
Parallel Axis Theorem | Perpendicular Axis Theorem |
Moment of Inertia about any axis is equal to the sum of the Moments of Inertia about an axis parallel to this axis, passing through the Centre Of Mass (COM) and the product of mass of the body with the square of the perpendicular distance between the axis in consideration and the COM axis parallel to it. | M.O.I of a body about an axis passing perpendicularly from it is equal to the sum of the M.O.I of the body about 2 mutually perpendicular axes lying in the plane of the object.
|
Io = IC + md2 Here, Io = M.O.I of shape about point O IC = M.O.I of shape about centroid ( C ) Md2 = Added M.O.I due to the distance between O and C. | IZZ = IXX + IYY |
This theorem is applicable for any object. There is no such restriction.
| This theorem applies only to the planar bodies that mean two-dimensional bodies. |
Q2) Explain dynamics?
A2)
Dynamics is the branch of mechanics that deals with the motion of the particle or a rigid body. In other words, dynamics deals with the accelerated motion of a body. Analysis in dynamics involves motion. Dynamics can be sub-divided into two parts:
- Kinematics
Kinematics is the branch of mechanics or simply a part of dynamic analysis which deals with the study or analysis of the motion of the body without considering the forces that causes this motion.
Hence Kinematics only analyses the geometry of the particle or rigid body.
2. Kinetics
Kinetics is the branch of mechanics or simply a part of dynamic analysis which deals with the study of motion of the body by considering the forces that causes this motion.
In other words, kinematics relates with the forces acting on the moving body.
Dynamics can be also classified on the basis of the body under study.
- Particle dynamics
Particle is nothing but a point body or a body who does not have any size and shape. Analysis of a particle in motion is referred to as particle dynamics
2. Rigid body dynamics
Rigid body is a body who does not change its shape and size when subjected to various forces and couples. Analysis of rigid body is referred to as rigid body dynamics
Q3) Differences between Moment Of Inertia and Polar Moment of Inertia
A3)
While the moment of inertia and polar moment of inertia sound similar they are two different quantities for measuring different properties of certain objects. We will look at a few differences below.
Moment Of Inertia | Polar Moment of Inertia |
Moment of inertia is used to measure an object’s ability to oppose angular acceleration. | It is a measurement of an object’s ability to oppose torsion. |
Its formula is given as I = r2 dm | It is defined as I or J = r2 dA |
It is measured in kg m2 | Its SI unit is m4 |
Depends on the mass of the body. | Depends on the geometry of the body |
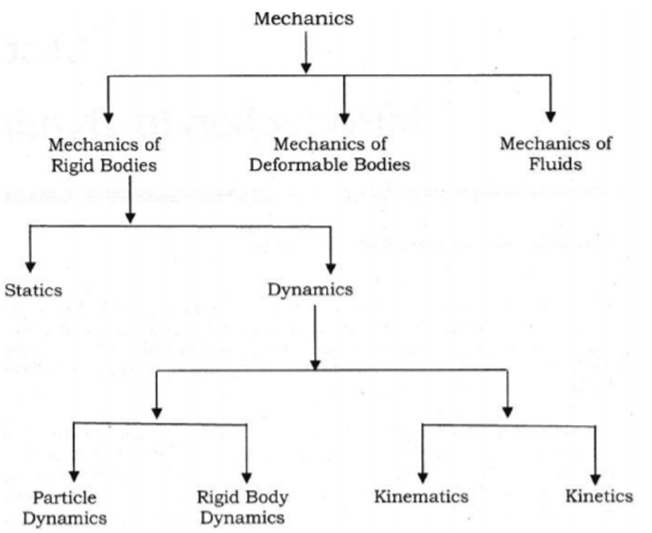
Q4) From a uniform circular disc of radius R and mass 9 M, a small disc of radius R/3 is removed as shown in the figure. Calculate the moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through the centre of the disc.
A4)
The moment of inertia of removed part abut the axis passing through the centre of mass and perpendicular to the plane of the disc = Icm + md2
= [m × (R/3)2]/2 + m × [4R2/9] = mR2/2
Therefore, the moment of inertia of the remaining portion = moment of inertia of the complete disc – moment of inertia of the removed portion
= 9mR2/2 – mR2/2 = 8mR2/2
Therefore, the moment of inertia of the remaining portion (I remaining) = 4mR2.
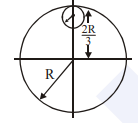
Q5) Moment Two balls connected by a rod, as shown in the figure below (Ignore rod’s mass). Mass of ball X is 700 grams and the mass of ball Y is 500 grams. What is the moment of inertia of the system about AB?
A5)
Given
The rotation axis is AB
mX = 700 grams = 0.7 kg
mY = 500 grams = 0.5 kg
rX = 10cm = 0.1m
rY = 40cm = 0.4m
Solution:
I = mX rX2 + mY rY2
I = (0.7)× (0.1)2 + (0.5)× (0.4)2
I = 7 × 10-3 + 0.08
I = 0.087 kg m2
Moment of inertia of the system is 0.087 kg m2
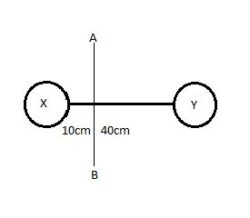
Q6) Two balls connected by a rod as shown in the figure below (Ignore rod’s mass). What is the moment of inertia of the system?
A6)
Given
mX = 300 grams = 0.3 kg
mY = 500 grams = 0.5 kg
rX = 0cm = 0m
rY = 30cm = 0.3m
Solution:
I = mX rX2 + mY rY2
I = (0.3)× (0)2 + (0.5)× (0.3)2
I = 0 + 0.045
I = 0.045 kg m2
Moment of inertia of the system is 0.045kg m2
Q7) The mass of each ball is 200 gram, connected by cord. The length of cord is 80 cm and the width of cord is 40 cm. What is the moment of inertia of the balls about the axis of rotation (Ignore cord’s mass).
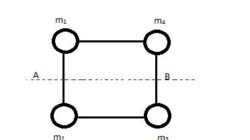
A7)
Given
Mass of ball = m1 = m2 = m3 = m4 = 200 gram = 0.2kg
Distance between ball and the axis of rotation (r1) = 40cm = 0.4 m
Distance between ball 2 and the axis of rotation (r2) = 40 cm = 0.4 m
Distance between ball 3 and the axis of rotation (r2) = 40 cm = 0.4 m
Distance between ball 4 and the axis of rotation (r2) = 40 cm = 0.4 m
Solu:
I = m1 r12 + m2 r22 + m3 r32 + m4 r42
I = (0.2) × (0.4)2 + (0.2) × (0.4 m)2 + (0.2) × (0.4)2 + (0.2) × (0.4)2
I = 0.032 + 0.032 + 0.032 + 0.032
I = 0.128 kg m2
Moment of inertia of the balls about the axis o.128 kg m2
Q8) What is the Difference between Static Friction and Kinetic Friction?
A8)
Static Friction | Kinetic Friction |
Static friction is the friction present between two or more objects that are not moving with respect to each other | Kinetic friction is the friction present between two or more objects that are in motion with respect to each other. |
The magnitude of static friction is greater due to the greater value of its coefficient | The magnitude of the kinetic friction is comparatively lesser due to the low value of its coefficient |
The equation representing static friction is given by Fs=μsη | The equation representing kinetic friction is given by Fk=μkη |
Q9) What is the difference between Kinetics and Kinematics?
A9)
Kinetics is focused on understanding the cause of different types of motions of an object such as rotational motion in which the object experiences force or torque.
Kinematics explains the terms such as acceleration, velocity, and position of objects. The mass of the object is not considered while studying the kinematics.
Difference Between Kinetics and Kinematics | |
Kinetics | Kinematics |
Deals with the causes for the motions of the object | Deals with the position, acceleration, speed of an object |
Takes into consideration the mass of the object | Doesn’t take into consideration the mass of the object |
Its practical applications can be found in the designing of automobiles | Its application can be found in the study of the movement of celestial bodies |
It takes forces explicitly into account | It doesn’t take forces explicitly into account |
It does not have more mathematical expressions | It has more mathematical expressions |
It is also known as dynamics | It is called with the same name |
This topic is used in various branches of science such as biology, chemistry and physics | This topic is used in physics, mechanics in terms of engineering |
Q10) Explain parallel axis theorem?
A10) Parallel Axis Theorem Derivation
Let Ic be the moment of inertia of an axis which is passing through the center of mass (AB from the figure) and I be the moment of inertia about the axis A’B’ at a distance of h.
Consider a particle of mass m at a distance r from the center of gravity of the body.
Then,
Distance from A’B’ = r + h
I = ∑m (r + h)2
I = ∑m (r2 + h2 + 2rh)
I = ∑mr2 + ∑mh2 + ∑2rh
I = Ic + h2∑m + 2h∑mr
I = Ic + Mh2 + 0
I = Ic + Mh2