UNIT 6
GENERAL MOTION
Q1) Explain Rigid body motion?
A1)
When all the particles of a rigid body move along paths which are equidistant from a fixed plane, the body is said to undergo planar motion.
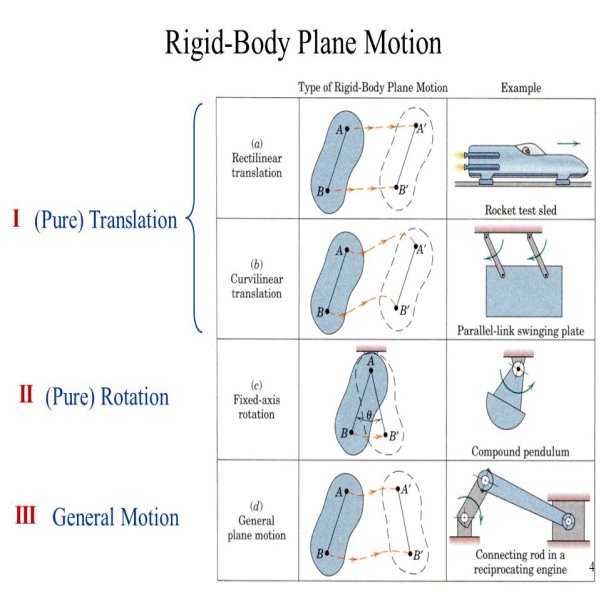
There are three types of rigid body planar motion
1. Translation: Every line segment in the body remains parallel to its original direction during the motion. Specifically, a body can undergo two types of translation:
(a) Rectilinear translation: All points follow parallel straight-line paths
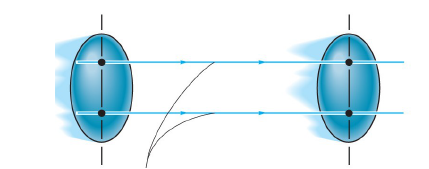
(b) Curvilinear translation: All points follow curved paths that are of the same shape and are equidistant from one another.
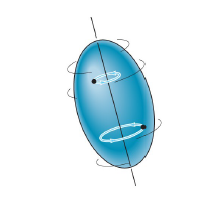
2. Rotation about a fixed axis: All the particles of the body, except those which lie on the axis of rotation move along circular paths
3. General plane motion: The body undergoes a combination of translation and rotation
All the above types of rigid body planar motion are exemplified by the moving parts of the crank mechanism shown in the figure below
Q2) Explain translation?
A2)
Translation:
Consider a rigid body which is subjected to either rectilinear or curvilinear translation in the x-y plane.
x’-y’ is a frame associated with the translating object.
A and B are two points in the rigid body. Because our object is a rigid body, all its points are at fixed distances from each other, moreover, for planar rigid body translation the direction ~rA/B is constant then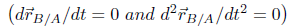 
. We have the following relations:
In other words, all the points on a translating rigid body move with the same velocity and acceleration
Q3) Explain Angular velocity?
A3)
Because all lines object B rotate at the same rate (at a given instant) B's rotation rate is the single number we call wB (omega b'). In order to make various formulas work out we dene a vector angular velocity with magnitude B which is perpendicular to the xy plane:
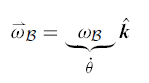
Where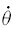 
is the rate of change of the angle of any line marked on object
B.
So long as you are careful to dene angular velocity by the rotation of line segments and not by the motion of individual particles, the concept of angular velocity in general motion is defined exactly as for a object rotating about a fixed axis. A legitimate way to think about planar motion of a rigid object is that any given point is moving in circles about any other given point (relative to that point). When a rigid object moves it always has an angular velocity (possibly zero).
If we call the object B (script B), we then call the object's angular velocity wB. In general it is best to use the sign convention that when B > 0 the object is rotating counter clockwise when viewed looking in from the positive z axis.
Q4) Explain General Plane motion?
A4)
General plane motion of a rigid body refers to a combination of translation and rotation motion.
General planar motion refers to the simultaneous rotational and translational motion of a planar body in a 2-D plane.
General planar motion can be fully specified by knowing both the angular rotation of a line fixed in the body and the motion of any point on the body.
These motions can be related by using a rectilinear position coordinate s to locate the point along its path and an angular position coordinate 
to specify the orientation of the line. Then these two coordinates are related using the geometry of the problem. The following relation is found.
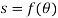
Differentiating the above equation, gives the relation between velocity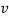 
and angular velocity 
.
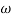Where,
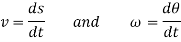
Then again differentiating, it yields to the relation between acceleration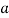 
and angular acceleration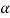 
Where,
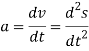
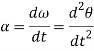
Q5) Explain Free precession?
A5)
For round objects rolling on or in another round object, the analysis is similar to that for rolling on a at surface. A common application is the so-called epicyclic, hypo-cyclic, or planetary gears on planetary gears. Referring to F we can calculate the velocity of C with respect to a fixed frame two ways and compare
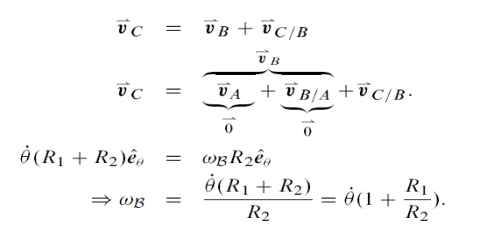
Example: Two quarters.
The formula above can be tested in the case of R1, R2 by using two quarters or
Two dimes on a table. Roll one quarter; call it B, around another quarter pressed
Fast to the table. You will see that as the rolling quarter B travels around the stationary quarter one time, it makes two full revolutions. That is, the orientation
Of B changes twice as fast as the angle of the line from the centre of the stationary quarter to its center. Or, in the language of the calculation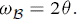 
Q6) Explain Application of General Plane Motion?
A6)
With the case of planar fixed axis rotation dealt with, we turn now to the more complex situation of general plane motion. Recall, once again, that the motion of an arbitrary rigid body can be reduced to the superposition of a translation and a fixed axis rotation. Handling the translation of a rigid body is trivial, all points of the body move with the same velocity and acceleration, and we now know how to deal with fixed axis rotations. Therefore, all that remains is to understand how the two are superposed. As we will find out, this is quite simple.
We proceed by returning to the equations we had derived for the arbitrary motion of a rigid body. Recall that these related the velocity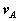 
and acceleration 
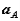of a point A in the body to the translational motion of an arbitrary reference point B (
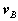and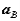 
), and the absolute rotational motion of the body (
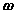and 
) as,
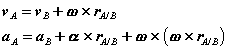
As in the case of fixed axis rotation we simplify these expressions by introducing a set of n-t coordinates. Unlike those used previously, however, the coordinates introduced here refer to the motion of A relative to the reference at B. Therefore,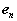 
is directed towards point B, the center of the relative motion, and 
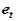is directed along 
, tangent to the path of A relative to B.
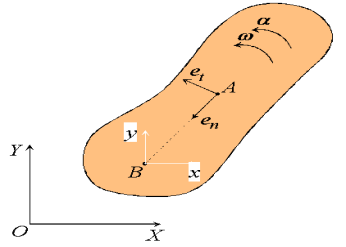
Figure: n-t coordinates for general plane motion.
Substituting, we obtain a simplified expression for the velocity of point A,
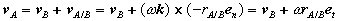
Which can be recognized as a superposition of translational and rotational components, each of which we understand very well.
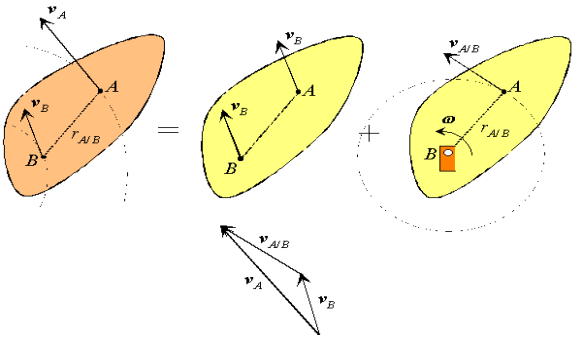
Figure: Decomposition of the absolute velocity of point A.
Proceeding in an analogous way for the acceleration,
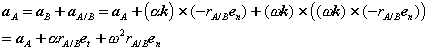
Or,
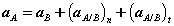
With normal and tangential accelerations of the form,
Therefore, like the velocity, the acceleration of A is a superposition of translational and rotational components. While the normal component is directed along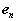 
, towards the axis of the rotational motion of A relative to B, the tangential component is directed along 
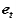, tangent to the path of A relative to B.
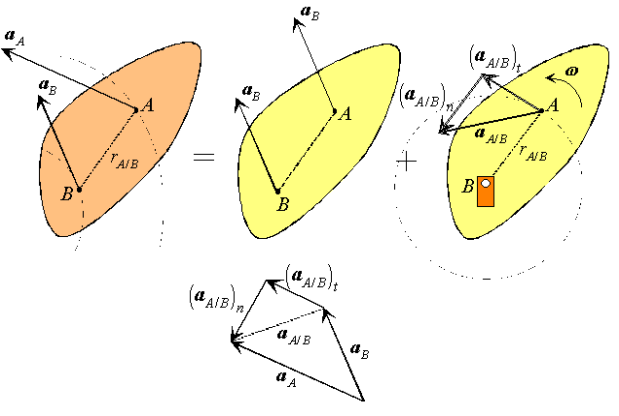
Figure: Decomposition of the absolute acceleration of point A.
For the general plane motion of a rigid body:
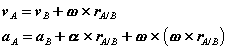
Alternately,
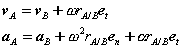
Where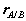 
is the position vector of A relative to the reference at B, 
, 
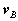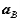are the velocity and acceleration of the reference and 
, 
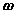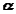are the angular velocity and acceleration of the body.
Q7) Describe Properties of Rigid Body Motion?
A7)
In the following, we identify two properties of the motion of rigid bodies that simplify the kinematics significantly. In order to do this, observe that an arbitrary rigid body motion falls into one of the three categories:
- Translation, rectilinear and curvilinear: Motion in which every line in the body remains parallel to its original position. The motion of the body is completely specified by the motion of any point in the body. All points of the body have the same velocity and same acceleration.
- Rotation about a fixed axis: All particles move in circular paths about the axis of rotation. The motion of the body is completely determined by the angular velocity of the rotation.
- General plane motion: Any plane motion that is neither a pure rotation nor a translation falls into this class. However, as we will see below, a general plane motion can always be reduced to the sum of a translation and a rotation.
We proceed by demonstrating that every motion of a planar rigid body is associated with a single angular velocity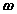 
and angular acceleration 
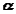, describing the angular displacement of an arbitrary line inscribed in the body relative to a fixed direction.
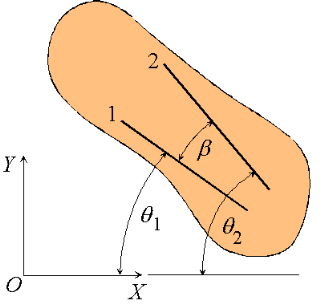
Figure: Angular velocity and acceleration of a rigid body.
Consider a rigid body undergoing plane motion. The angular positions of two arbitrary lines 1 and 2 attached to the body are specified by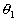 
and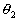 
measured relative to any convenient fixed reference direction. These are related to the intermediate angle 
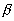shown as,
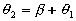
Observe that as the body is rigid, requiring that the distance between each pair of points on the two lines 1 and 2 is constant, angle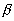 
must be invariant. Differentiating the relation above with this in mind,
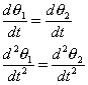
These hold for arbitrary lines attached to the body, implying in turn that the body can be associated with a unique angular velocity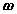 
, defined as,
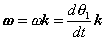
For an arbitrary line attached to the body. Arguing analogously, the body can be associated with a unique angular acceleration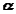 
defined as,
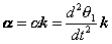
Figure: Angular velocity and angular acceleration of a rigid body.
Consequently, we have the property that all lines on a rigid body in its plane of motion have the same angular displacement, the same angular velocity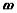 
and the same angular acceleration
.
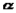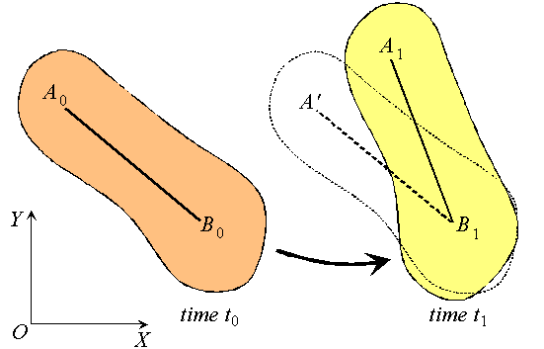
Figure: Decomposition of rigid body motion.
Next, consider the motion of a rigid body over the interval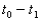 
as shown, with arbitrary point 
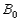taken as reference. Clearly, the motion can be consider to occur in two stages: a translation with reference 
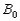taking arbitrary line 
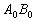to an intermediate position
; and a rotation about point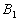 
taking 
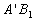to its final position 
. This corresponds to a decomposition of the motion into the sum of a translation and a rotation. While the translational motion is described by the velocity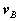 
and acceleration 
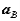of the reference point, the rotational motion is characterized by the unique angular velocity 
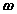and angular acceleration 
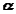associated with the body. Thus, we have the property that the motion of a rigid body can be decomposed into a translation of an arbitrary point within the body, followed by a rigid rotation of the body about this point. Further, the motion of an arbitrary point within the body is determined completely once the translational quantities 
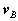and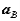
, and rotational quantities 
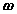and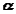 
are known.
Characteristics of rigid body motion:
- All lines on a rigid body have the same angular velocity
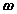and the same angular acceleration
.
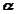Rigid motion can be decomposed into the translation of an arbitrary point, followed by a rotation about the point.
Q8) The motor M begins rotating at ω = 4(1 – e-t) rad/s, where t is in seconds.
The radii of the motor, fan pulleys, and fan blades are 1 in, 4 in, and 16 in, respectively.
Find the magnitudes of the velocity and acceleration at point P on the fan blade when t = 0.5 s.?
A8)
1) Determine the angular velocity and acceleration of the motor using kinematics of angular motion.
2) Assuming the belt does not slip, the angular velocity and acceleration of the fan are related to the motor's values by the belt.
3) The magnitudes of the velocity and acceleration of point P can be determined from the scalar equations of motion for a point on a rotating body.
1) Since the angular velocity is given as a function of time, ωm = 4(1 – e-t), the angular acceleration can be found by differentiation.
αm = dωm/dt = 4e-t rad/s2
When t = 0.5 s,
ωm = 4(1 – e-0.5) = 1.5739 rad/s, αm = 4e-0.5 = 2.4261 rad/s2
2) Since the belt does not slip (and is assumed inextensible), it must have the same speed and tangential component of acceleration at all points. Thus the pulleys must have the same speed and tangential acceleration at their contact points with the belt. Therefore, the angular velocities of the motor (ωm) and fan (ωf) are related as
v = ωm rm = ωf rf => (1.5739)(1) = ωf(4) => ωf = 0.3935 rad/s
3) Similarly, the tangential accelerations are related as
at = αm rm = αf rf => (2.4261)(1) = αf(4) => αf = 0.6065 rad/s2
4) The speed of point P on the the fan, at a radius of 16 in, is now determined as
vP = ωfrP = (0.3935)(16) = 6.30 in/s
The normal and tangential components of acceleration of point
P are calculated as
An = (ωf)2 rP = (0.3935)2 (16) = 2.477 in/s2
At = αf rP = (0.6065) (16) = 9.704 in/s2
The magnitude of the acceleration of P can be determined by
AP = √ [(an)2 + (at)2 ]= √ [(2.477)2 + (9.704)2 ]= 10.0 in/s2
Q9) Rigid body planar motion?
A9)
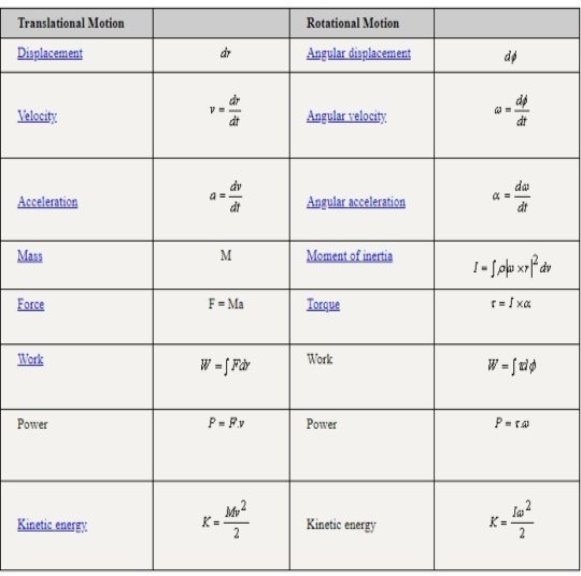
Q10) Symbolic difference between translation and rotational motion?
A10)
