UNIT 9
FRICTION
Q1) A large block of ice is being pulled across a frozen lake. The block of ice has a mass of 300 kg. The coefficient of friction between two ice surfaces is small: μk = 0.05. What is the force of friction that is acting on the block of ice?
A1)
On a flat surface, the normal force on an object is given by N = mg. With this, we can find the force of friction as follows:
Ff =μN
Ff =μmg
Substituting the values in the above equation we get,
Ff =0.05 × 300 kg × 9.8 m/s2
=157 kg-m/s2 or 157 N.
The force of friction acting in the opposite direction as the block of ice is pulled across the lake is 157 N.
Q2) A man has to push his boat on the shore across the mud to get to the water. The coefficient of friction between the boat and the mud is given by μ = 0.400. If the boat has a mass of 40 kg, calculate the magnitude of the force of friction acting on the boat.
A2)
On a flat surface, the normal force on an object is N = mg. Using this, we can calculate the force of friction as follows
F = μN
F = μ mg
Substituting the values in the equation, we ge
t F = (0.400)(40.0 kg)(9.80 m/s2)
F = 156.8 N
The frictional force acting on the boat is 156.8 N.
Q3) What is the Difference Between Static Friction and Kinetic Friction?
A3)
Static Friction | Kinetic Friction |
Static friction is the friction present between two or more objects that are not moving with respect to each other | Kinetic friction is the friction present between two or more objects that are in motion with respect to each other. |
The magnitude of static friction is greater due to the greater value of its coefficient | The magnitude of the kinetic friction is comparatively lesser due to the low value of its coefficient |
The equation representing static friction is given by Fs=μsη | The equation representing kinetic friction is given by Fk=μkη |
Q4) A man pushes large cardboard of mass 75.0 kg box across the floor. The coefficient of kinetic friction is μk = 0.520. The worker exerts a force of 400.0 N forward. What is the magnitude of the force of friction?
A4)
On a flat surface, the normal force of an object can be found out by the formula
η =mg (1)
By substituting the value of η in the equation Fk=μk η, we get
Fk= (0.520)(75.0kg)(9.80m/s2) = 382.2N
The net force acting on a body is the sum of all the forces acting on the body. In this case, the forces acting on the body are the force exerted by the man and the kinetic friction acting in the opposite direction. If the forward motion is considered positive, then the net force is calculated as follows:
Fnet = Fworker – FK
Substituting the values in the above equation, we get
Fnet = 400 N – 382.2 N = 17.8 N
Q5) Define angle of friction and angle of repose Show that angle of friction is equal to angle of repose?
A5) Angle of friction (φ): Angle made by the resultant of normal reaction and limiting frictional force with the normal reaction is called angle of friction.
Angle of repose (θ): The minimum angle of the plane at which the body kept on it starts to slide due to its own weight is called angle of repose
To prove: θ=φ
∑ F.y=0
N−Wcosθ=0
N=Wcosθ
∑Fx=0
−Wsinθ+F=0
F=Wsinθ
µN=Wsinθ
µWcosθ=Wsinθ
µ=tanθ
But µ=tanφ
Tanφ=tanθ
φ=θ proved
Q6) Dimensional Formula of Coefficient of Friction?
A6)
The dimensional formula of coefficient of friction is given by,
[M0 L0 T0]
Where,
- M = Mass
- L = Length
- T = Time
Derivation
Coefficient of friction (μ) = Frictional Force × [Normal Force]-1 . . . . (1)
Since, Force (F) = Mass × acceleration = Mass × velocity × [Time]-1
And, velocity = Displacement × [Time]-1
∴ The dimensions of Force = [M] × [LT-1] × [T]-1 = [M1 L1 T-2] . . . . (2)
On substituting equation (2) in equation (1) we get,
Coefficient of friction (μ) = Frictional Force × [Normal Force]-1
Or, μ = [M1 L1 T-2] × [M1 L1 T-2]-1 = [M0 L0 T0].
Therefore, the coefficient of friction is dimensionally represented as [M0 L0 T0].
Q7) An object of mass 10 kg is moving through a surface. Compute the friction force if the coefficient of friction is 0.2?
A7)
Known variables are:
m = 10 kg and μ = 0.2
The friction force formula is,
Ff = μFn
Fn can be computed as,
Fn = mg
= 10×9.81 = 98.1 N
So, Ff = 0.2×98.1 = 19.62 N
Friction force Ff is 19.62 N
Q8) Calculate the friction force of a 5 kg body which is moving through a surface with a friction coefficient 0.3?
A8)
Known variables are,
m = 5 kg and μ = 0.3
The friction force formula is,
Ff = μFn
Fn can be computed as,
Fn = mg
= 5×9.81 = 49.05 N
So, Ff = 0.3×49.05 = 14.715 N
Friction force Ff is 14.715 N
Q8) Explain angle of friction and angle of kinetic friction?
A9)
- A9) Angle of Friction (
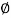 ) :
) :
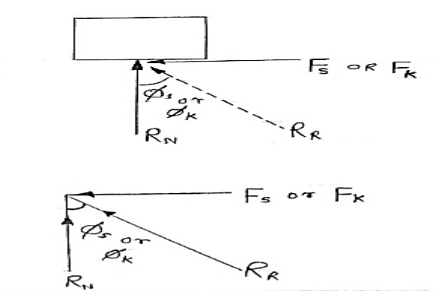
Angle of static Friction ( S) :
S) :
For the body at rest, the angle between
Normal reaction and resultant reaction
Is called as angle of static friction (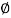 S)
S)
 tan (
tan (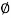 S) =
S) = 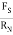
 tan
tan 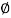 S =
S = 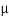 S
S
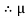 S =tan
S =tan 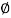 Sand
Sand
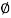 S = tan-1
S = tan-1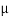 S
S
- Angle of kinetic friction (
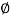 K) :
K) :
For the body in motion, angle made by normal reaction with resultant is called as angle of kinetic friction ( K)
K)
 tan (
tan (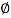 K) =
K) = 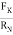
 tan
tan 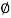 K =
K = 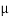 K
K
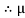 K =tan
K =tan 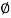 K and
K and
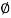 K = tan-1
K = tan-1 K
K
Q9) A block of mass m rests on frictional plane which makes an angle 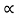 with horizontal as shown if the coefficient. Of friction between the block & frictional plane is 0.2, determine angle
with horizontal as shown if the coefficient. Of friction between the block & frictional plane is 0.2, determine angle 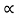 for limiting friction?
for limiting friction?
A10)
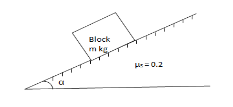
For limiting friction
Tan 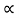 tan
tan 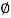 S =
S = 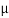 S
S
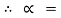 tan-1
tan-1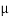 S
S
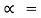 tan-1
tan-1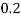
 11.310
11.310