Unit-1
Basic probability
Q1) A factory has two machines A and B making 60% and 40% respectively of the total production. Machine A produces 3% defective items, and B produces 5% defective items. Find the probability that a given defective part came from A.
S1)
We consider the following events:
A: Selected item comes from A.
B: Selected item comes from B.
D: Selected item is defective.
We are looking for 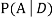 . We know:
. We know:
 Now, 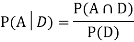 So we need 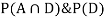
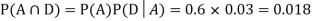
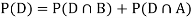
Since, D is the union of the mutually exclusive events 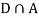 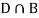
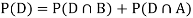
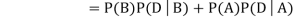
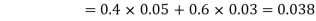
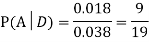
|
Q2) Three urns contain 6 red, 4 black; 4 red, 6 black; 5 red, 5 black balls respectively. One of the urns is selected at random and a ball is drawn from it. If the ball drawn is red find the probability that it is drawn from the first urn.
S2)
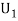 :The ball is drawn from urnI.
:The ball is drawn from urnI.
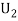 : The ball is drawn from urnII.
: The ball is drawn from urnII.
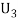 : The ball is drawn from urnIII.
: The ball is drawn from urnIII.
R:The ball is red.
We have to find 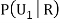
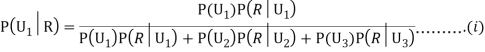
Since the three urns are equally likely to be selected
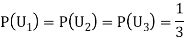 Also, 
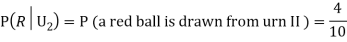
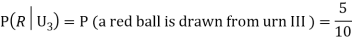
From (i), we have
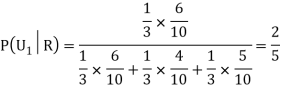
|
Q3) A random variable x has the following probability distribution-
 |
Then find-
1. Value of c.
2. P[X≤3]
3. P[1 < X <4]
S3)
We know that for the given probability distribution-
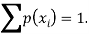 So that- 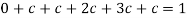 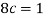 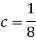 2. 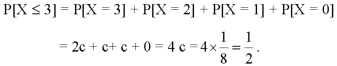 3. 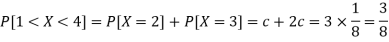
|
Q4) You are given a bag of marble. Inside the bag are 5 red marble, 4 white marble, 3 blue marble. Calculate the probability that with 6 trials you choose 3 marbles that are red, 1 marble that is white and 2 marble is blue. Replacing each marble after it is chosen.
S4)
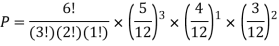
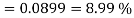 |
Q5) If the probability of a bad reaction from a certain injection is 0.001, determine the chance that out of 2,000 individuals more than to get a bad reaction.
S5) It follows a Poisson distribution as the probability of occurrence is very small
Mean m = np = (0.001)=2
Probability that more than two will get bad reaction
= 1- [probability that no one get a bad reaction + probability that one gets a bad reaction + probability that to get bad reaction]
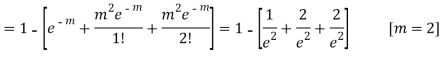  |
Q6) Fit a Poisson distribution to the set of observations:
x | 0 | 1 | 2 | 3 | 4 |
f | 122 | 60 | 15 | 2 | 1 |
S6)
Mean = 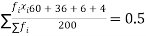
Therefore mean of Poisson distribution i.e. m =0.5
Hence the theoretical frequency for r successes is is
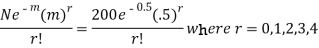
Therefore the theoretical frequencies are
x | 0 | 1 | 2 | 3 | 4 |
f | 121 | 61 | 16 | 2 | 0 |
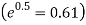
Q7) 10 coins are tossed simultaneously where the probability of getting heads for each coin is 0.6. Find the probability of obtaining 4 heads.
S7)
Probability of obtaining the head, p = 0.6
Probability of obtaining the head, q = 1 - p = 1 - 0.6 = 0.4
Probability of obtaining 4 of 10 heads, P (X = 4) = C104 (0.6) 4 (0.4) 6P (X = 4) = C410 (0.6) 4 (0.4) 6 = 0.111476736
Q8) I toss a coin twice and define X to be the number of heads one observe. Then I toss the coin two more times and define Y to be the number of heads that I observed this time. Find 
S8) since X and Y are the result of different independent coin tosses the two random variables X and Y are independent.
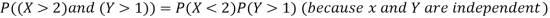 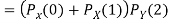 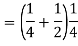 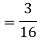
|
Q9) (a) A biased coin is tossed till a head appears for the first time. What is the probability that the number of required tosses is odd?
(b) Two persons A and B toss an unbiased coin alternately on the understanding that the first two who get the head wins. If A starts the game, find their respective chances of winning.
S9) (a) Let p be the probability of getting a head and q the probability of getting a tail in a single toss, so that p + q=1.
Then probability of getting head on an odd toss = probability of getting gead in the 3rd toss + probability of getting head in the 5th toss +…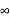
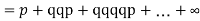  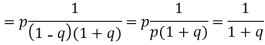 (b) Probability of getting head = 1/2 . Then A can win in 1st, 3rd, 5th,…throws. The chances of A’s winning = 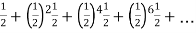  Hence the chances of B’s winning= 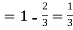 |
Q10) Two cards are drawn in succession from a pack of 52 cards. Find the chance that the first is a king and the second a queen if the first card is
(i) Replaced
(ii) Got replaced
S10) (i) the probability of drawing a king 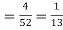
If the card is replaced the back will again have 52 cards so that the probability of drawing a queen is 1/13.
The two events being independent the probability of drawing both cards in succession 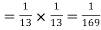
(ii)the probability of drawing a king = 1/13
If the card is not replaced the pack will have 51 cards only so that the chance of drawing the queen is 4/51.
Hence the probability of drawing both cards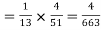
Q11) X is a continuous random variable with probability density function given by


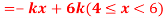
Find k and mean value of X.
S11) Since the total probability is unity.
 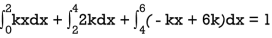 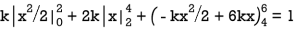  Mean of X = 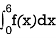 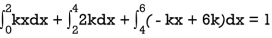 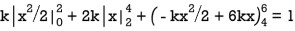 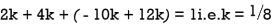 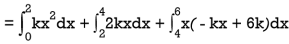 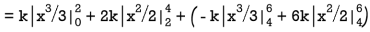 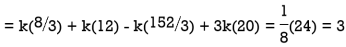
|
Q12) Find the moment generating function of the exponential distribution 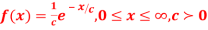 . Hence find its mean and S.D.
. Hence find its mean and S.D.
S12) The moment generating function about the origin is
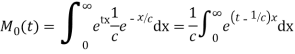 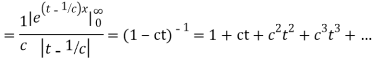 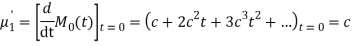 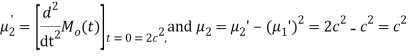 Hence the mean is c wand S.D. Is also c |
Q13) I roll a fair die and let X be the resulting number. Find EX, Var(X), and 
S13) We have  and
and 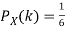 for k = 1,2,…,6. Thus we have
for k = 1,2,…,6. Thus we have
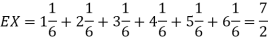 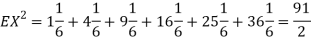 Thus , 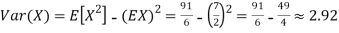 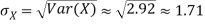 |
Q14) Find the correlation coefficient between Age and weight of the following data-
Age | 30 | 44 | 45 | 43 | 34 | 44 |
Weight | 56 | 55 | 60 | 64 | 62 | 63 |
S14)
x | y | 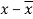 | 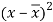 |  | 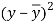 | ( 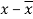 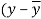 |
30 | 56 | -10 | 100 | -4 | 16 | 40 |
44 | 55 | 4 | 16 | -5 | 25 | -20 |
45 | 60 | 5 | 25 | 0 | 0 | 0 |
43 | 64 | 3 | 9 | 4 | 16 | 12 |
34 | 62 | -6 | 36 | 2 | 4 | -12 |
44 | 63 | 4 | 16 | 3 | 9 | 12 |
Sum= 240 |
360 |
0 |
202 |
0 |
70
|
32 |
Karl Pearson’s coefficient of correlation-
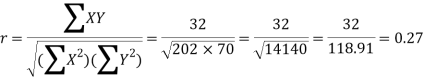
|
Here the correlation coefficient is 0.27.which is the positive correlation (weak positive correlation), this indicates that the as age increases, the weight also increase.
Q15) Ten students got the following percentage of marks in Economics and Statistics
Calculate the  of correlation.
of correlation.
Roll No. |  |  |  |  |  |  |  |  |  |  |
Marks in Economics |  |  |  |  |  |  |  |  |  |  |
Marks in  |  |  |  |  |  |  |  |  |  |  |
S15)
Let the marks oftwo subjects be denoted by 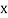 and
and  respectively.
respectively.
Then the mean for 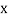 marks
marks  and the mean ofy marks
and the mean ofy marks 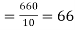
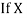 and
and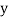 are deviations ofx’s and
are deviations ofx’s and 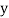 ’s from their respective means, then the data may be arranged in the following form:
’s from their respective means, then the data may be arranged in the following form:
x | y | X=x=65 | Y=y=66 | 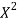 | 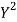 | XY |
78 | 84 | 13 | 18 | 169 | 234 | 234 |
36 | 51 | -29 | -15 | 841 | 225 | 435 |
98 | 91 | 33 | 1089 | 1089 | 625 | 825 |
25 | 60 | -40 | 1600 | 1600 | 36 | 240 |
75 | 68 | 10 | 100 | 100 | 4 | 20 |
82 | 62 | 17 | 289 | 289 | 16 | -68 |
90 | 86 | 25 | 625 | 625 | 400 | 500 |
62 | 58 | -3 | 9 | 9 | 64 | 24 |
65 | 53 | 0 | 0 | 0 | 169 | 0 |
39 | 47 | -26 | 676 | 676 | 361 | 494 |
650 | 660 | 0 | 5398 | 5398 | 2224 | 2704 |
Here, 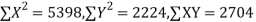
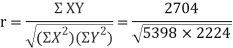

Q16) Compute Spearman’s rank correlation coefficient r for the following data:
Person | A | B | C | D | E | F | G | H | I | J |
Rank Statistics | 9 | 10 | 6 | 5 | 7 | 2 | 4 | 8 | 1 | 3 |
Rank in income | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
S16)
Person | Rank Statistics | Rank in income | d= 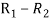 | 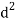 |
A | 9 | 1 | 8 | 64 |
B | 10 | 2 | 8 | 64 |
C | 6 | 3 | 3 | 9 |
D | 5 | 4 | 1 | 1 |
E | 7 | 5 | 2 | 4 |
F | 2 | 6 | -4 | 16 |
G | 4 | 7 | -3 | 9 |
H | 8 | 8 | 0 | 0 |
I | 1 | 9 | -8 | 64 |
J | 3 | 10 | -7 | 49 |
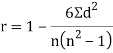
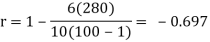
Q17) Let X ~ binomial (n, p). Using Markov's inequality, find an upper bound on P(X ≥ n), where
n), where  . Evaluate the ground for
. Evaluate the ground for 
S17)
Note that X is a non negative random variable and EX = np. Applying Markov's inequality we obtain
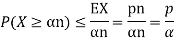
For 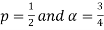 ,we obtain
,we obtain
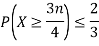
Q18) Let X ~ binomial (n, p). Using Chebyshev's inequality, find an upper bound on P(X ≥n), where  . Evaluate the ground for
. Evaluate the ground for 
S18)
One way to obtain a bound is to write
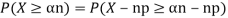
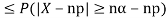
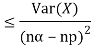
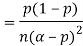
For p = ½ and 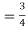 , we obtain
, we obtain