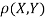Unit-3
Bivariate Distributions
Q1) Let  be two independent N (0, 1) random variables. Define
be two independent N (0, 1) random variables. Define
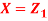
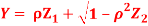
Where  is a real number in (-1, 1).
is a real number in (-1, 1).
- Show that X and Y are bivariate normal.
- Find the joint PDF of X and Y.
- Find
 (X,Y)
(X,Y)
S1)
First note that since 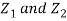 are normal and independent they are jointly normal with the joint PDF
are normal and independent they are jointly normal with the joint PDF

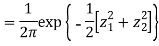
- We need to show aX + bY is normal for all. We have
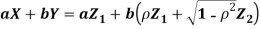
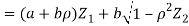
Which is the linear combination of  and thus it is normal.
and thus it is normal.
b. We can use the method of transformations (theorem 5.1) to find the joint PDF of X and Y. The inverse transformation is given by
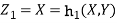 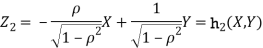 We have  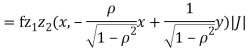 Where, 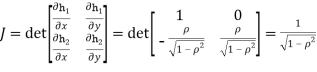 Thus we conclude that 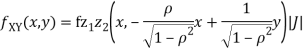 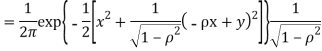 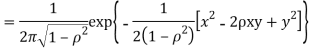
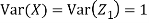 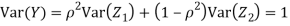 Therefore, 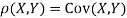  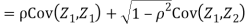 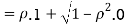 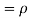
|
Q2) Let X and Y be jointly normal random variables with parameters  Find the conditional distribution of Y given X =x.
Find the conditional distribution of Y given X =x.
S2) One way to solve this problem is by using the joint PDF formula since X N
N  we can use
we can use
  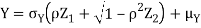 Thus given X=x, we have 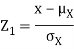 And, 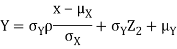 Since 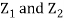 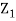 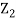 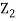 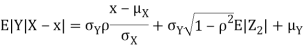 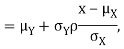 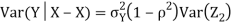  We conclude that given X=x,Y is normally distributed with mean  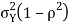
|
Q3) A die is tossed thrice. A success is getting 1 or 6 on a toss. Find the mean and variance of the number of successes.
S3)
Probability of success  probability of failures
probability of failures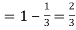
Probability of no success= probability of all three failures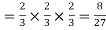
Probability of one successes and two failures 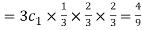
Probability of Two successes and one failure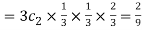
Probability of three successes 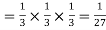
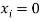 | 1 | 2 | 3 |
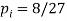 | 4/9 | 2/9 | 1/27 |
Mean 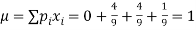
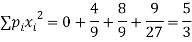
Variance,
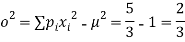
Q4) The probability density function of a variate X is
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
P (X) | k | 3k | 5k | 7k | 9k | 11k | 13k |
S4) (I) If X is random variable then
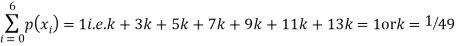 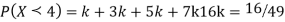 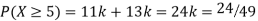 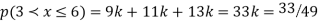 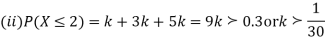  |
Q5) Random variable X has the following probability function
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P (x) | 0 | k | 2k | 2k | 3k | 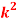 | 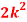 | 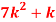 |
(i) Find the value of the k
(ii) Evaluate P (X < 6), P (X≥6)
(iii) 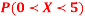
S5) (i) if X is a random variable then

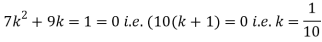
(ii)P (X < 6) =P( X=0) +P(X=1)+P(X=2)+ P(X=3) +P(X=4) + P (X=5)
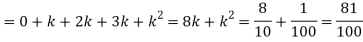
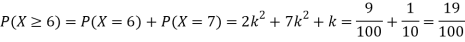
(iv) 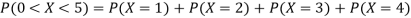
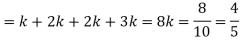
Q6) A bag contains 12 pens of which 4 are defective. Three pens are picked at random from the bag one after the other.
Then find the probability that all three are non-defective.
S6) here the probability of the first which will be non-defective = 8/12
By the multiplication theorem of probability,
If we draw pens one after the other then the required probability will be-
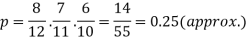
Q7) An urn  contains 3 white and 4 red balls and an urn lI contains 5 white and 6 red balls. One ball is drawn at random from one ofthe urns and isfound to be white. Find the probability that it was drawn from urn 1.
contains 3 white and 4 red balls and an urn lI contains 5 white and 6 red balls. One ball is drawn at random from one ofthe urns and isfound to be white. Find the probability that it was drawn from urn 1.
S7) Let 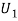 : the ball is drawn from urn I
: the ball is drawn from urn I
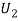 : the ball is drawn from urn II
: the ball is drawn from urn II
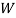 : the ball is white.
: the ball is white.
We have to find 
By Bayes Theorem
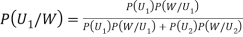 ... (1)
... (1)
Since two urns are equally likely to be selected,  (a white ball is drawn from urn
(a white ball is drawn from urn 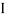 )
) 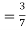
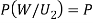 (a white ball is drawn from urn II)
(a white ball is drawn from urn II) 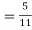
From(1), 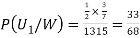
Q8) Three urns contains 6 red, 4 black, 4 red, 6 black; 5 red, 5 black balls respectively. One of the urns is selected at random and a ball is drawn from it. Lf the ball drawn is red find the probability that it is drawn from the first turn.
S8)
Let 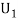 : the ball is drawn from urn 1.
: the ball is drawn from urn 1.
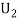 : the ball is drawn from urn lI.
: the ball is drawn from urn lI.
 : the ball is drawn from urn 111.
: the ball is drawn from urn 111.
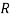 : the ball is red.
: the ball is red.
We have to find 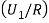 .
.
By Baye’s Theorem,  Since the three urns are equally likely to be selected 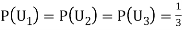 Also 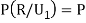     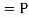 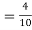 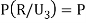 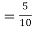 From (1), we have 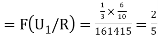
|
Q9) ln a bolt factory machines  and
and  manufacturerespectively 25%, 35% and 40% of the total. Lf their output 5, 4 and 2 per cent are defective bolts. A bolt is drawn at random from the product and is found to be defective. What is the probability that it was manufactured by machine B.
manufacturerespectively 25%, 35% and 40% of the total. Lf their output 5, 4 and 2 per cent are defective bolts. A bolt is drawn at random from the product and is found to be defective. What is the probability that it was manufactured by machine B. ?
?
S9) bolt is manufactured by machine 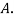
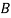 : bolt is manufactured by machine
: bolt is manufactured by machine 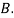
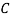 : bolt is manufactured by machine
: bolt is manufactured by machine 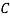

The probability of drawing a defective bolt manufactured by machine 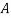 is
is 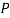 (D/A)
(D/A) 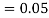
Similarly, 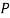 (D/B)
(D/B) 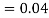 and
and 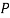 (D/C)
(D/C) 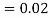
By Bayes’ theorem
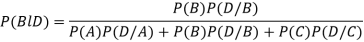 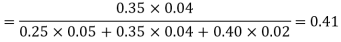
|