Unit-6
Small samples
Q1) A company of pens claims that a certain pen manufactured by him has a mean writing-life at least 460 A-4 size pages. A purchasing agent selects a sample of 100 pens and put them on the test. The mean writing-life of the sample found 453 A-4 size pages with standard deviation 25 A-4 size pages. Should the purchasing agent reject the manufacturer’s claim at 1% level of significance?
S1)
It is given that-
Specified value of population mean = 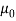 = 460,
= 460,
Sample size = 100
Sample mean = 453
Sample standard deviation = S = 25
 |
The null and alternative hypothesis will be-
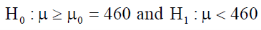
Also the alternative hypothesis left-tailed so that the test is left tailed test.
Here, we want to test the hypothesis regarding population mean when population SD is unknown. So we should used t-test for if writing-life of pen follows normal distribution. But it is not the case. Since sample size is n = 100 (n > 30) large so we go for Z-test. The test statistic of Z-test is given by

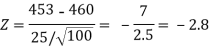
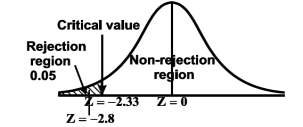
We get the critical value of left tailed Z test at 1% level of significance is 
Since calculated value of test statistic Z (= ‒2.8) is less than the critical value
(= −2.33), that means calculated value of test statistic Z lies in rejection region so we reject the null hypothesis. Since the null hypothesis is the claim so we reject the manufacturer’s claim at 1% level of significance.
Q2) A big company uses thousands of CFL lights every year. The brand that the company has been using in the past has average life of 1200 hours. A new brand is offered to the company at a price lower than they are paying for the old brand. Consequently, a sample of 100 CFL light of new brand is tested which yields an average life of 1220 hours with standard deviation 90 hours. Should the company accept the new brand at 5% level of significance?
S2)
Here we have-
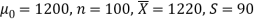
The company may accept the new CFL light when average life of
CFL light is greater than 1200 hours. So the company wants to test that the new brand CFL light has an average life greater than 1200 hours. So our claim is 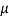 > 1200 and its complement is
> 1200 and its complement is 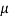 ≤ 1200. Since complement contains the equality sign so we can take the complement as the null hypothesis and the claim as the alternative hypothesis. Thus,
≤ 1200. Since complement contains the equality sign so we can take the complement as the null hypothesis and the claim as the alternative hypothesis. Thus,
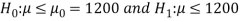
Since the alternative hypothesis is right-tailed so the test is right-tailed test.
Here, we want to test the hypothesis regarding population mean when population SD is unknown, so we should use t-test if the distribution of life of bulbs known to be normal. But it is not the case. Since the sample size is large (n > 30) so we can go for Z-test instead of t-test.
Therefore, test statistic is given by
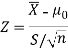
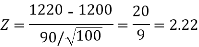
The critical values for right-tailed test at 5% level of significance is
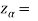 1.645
1.645
Since calculated value of test statistic Z (= 2.22) is greater than critical value (= 1.645), that means it lies in rejection region so we reject the null hypothesis and support the alternative hypothesis i.e. we support our claim at 5% level of significance
Thus, we conclude that sample does not provide us sufficient evidence against the claim so we may assume that the company accepts the new brand of bulbs
Q3) Eleven students were given a test in statistics. They were given a month’s further tuition and the second test of equal difficulty was held at the end of this. Do the marks give evidence that the students have benefitted by extra coaching?
Boys | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Marks I test | 23 | 20 | 19 | 21 | 18 | 20 | 18 | 17 | 23 | 16 | 19 |
Marks II test | 24 | 19 | 22 | 18 | 20 | 22 | 20 | 20 | 23 | 20 | 17 |
S3) We compute the mean and the S.D. Of the difference between the marks of the two tests as under:
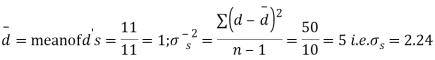
|
Assuming that the students have not been benefitted by extra coaching, it implies that the mean of the difference between the marks of the two tests is zero i.e.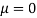
Then, 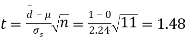 nearly and df v=11-1=10
nearly and df v=11-1=10
Students | 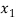 | 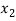 | 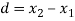 | 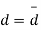 |  |
1 | 23 | 24 | 1 | 0 | 0 |
2 | 20 | 19 | -1 | -2 | 4 |
3 | 19 | 22 | 3 | 2 | 4 |
4 | 21 | 18 | -3 | -4 | 16 |
5 | 18 | 20 | 2 | 1 | 1 |
6 | 20 | 22 | 2 | 1 | 1 |
7 | 18 | 20 | 2 | 1 | 1 |
8 | 17 | 20 | 3 | 2 | 4 |
9 | 23 | 23 | - | -1 | 1 |
10 | 16 | 20 | 4 | 3 | 9 |
11 | 19 | 17 | -2 | -3 | 9 |
|
|
| 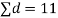 |
| 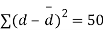 |
We find that 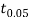 (for v=10) =2.228. As the calculated value of
(for v=10) =2.228. As the calculated value of 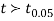 , the value of t is not significant at 5% level of significance i.e. the test provides no evidence that the students have benefitted by extra coaching.
, the value of t is not significant at 5% level of significance i.e. the test provides no evidence that the students have benefitted by extra coaching.
Q4) From a random sample of 10 pigs fed on diet A, the increase in weight in certain period were 10,6,16,17,13,12,8,14,15,9 lbs. For another random sample of 12 pigs fed on diet B, the increase in the same period were 7,13,22,15,12,14,18,8,21,23,10,17 lbs. Test whether diets A and B differ significantly as regards their effect on increases in weight ?
S4) We calculate the means and standard derivations of the samples as follows
| Diet A |
|
| Diet B |
|
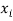 | 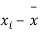 | 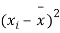 | 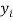 | 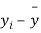 | 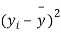 |
10 | -2 | 4 | 7 | -8 | 64 |
6 | -6 | 36 | 13 | -2 | 4 |
16 | 4 | 16 | 22 | 7 | 49 |
17 | 5 | 25 | 15 | 0 | 0 |
13 | 1 | 1 | 12 | -3 | 9 |
12 | 0 | 0 | 14 | -1 | 1 |
8 | -4 | 16 | 18 | 3 | 9 |
14 | 2 | 4 | 8 | -7 | 49 |
15 | 3 | 9 | 21 | 6 | 36 |
9 | -3 | 9 | 23 | 8 | 64 |
|
|
| 10 | -5 | 25 |
|
|
| 17 | 2 | 4 |
|
|
|
|
|
|
120 |
|
| 180 | 0 | 314 |


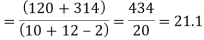
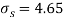
Assuming that the samples do not differ in weight so far as the two diets are concerned i.e. 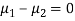
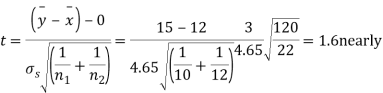

For v=20, we find 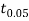 =2.09
=2.09
The calculated value of 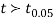
Hence the difference between the samples means is not significant i.e. thew two diets do not differ significantly as regards their effects on increase in weight.
Q5) A college conducts both face to face and distance mode classes for a particular course indented both to be identical. A sample of 50 students of face to face mode yields examination results mean and SD respectively as-

And other sample of 100 distance-mode students yields mean and SD of their examination results in the same course respectively as:

Are both educational methods statistically equal at 5% level?
S5) here we have-
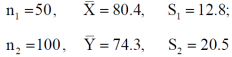
Here we wish to test that both educational methods are statistically equal. If 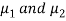 denote the average marks of face to face and distance mode students respectively then our claim is
denote the average marks of face to face and distance mode students respectively then our claim is 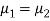 and its complement is
and its complement is  ≠
≠  . Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,
. Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,
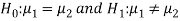
Since the alternative hypothesis is two-tailed so the test is two-tailed test.
We want to test the null hypothesis regarding two population means when standard deviations of both populations are unknown. So we should go for t-test if population of difference is known to be normal. But it is not the case.
Since sample sizes are large (n1, and n2 > 30) so we go for Z-test.
For testing the null hypothesis, the test statistic Z is given by
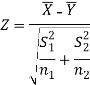

The critical (tabulated) values for two-tailed test at 5% level of significance are-
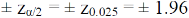
Since calculated value of Z ( = 2.23) is greater than the critical values
(= ±1.96), that means it lies in rejection region so we
Reject the null hypothesis i.e. we reject the claim at 5% level of significance
Q6) A set of five similar coins is tossed 320 times and the result is
Number of heads | 0 | 1 | 2 | 3 | 4 | 5 |
Frequency | 6 | 27 | 72 | 112 | 71 | 32 |
S6) For v = 5, we have 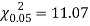
P, probability of getting a head=1/2;q, probability of getting a tail=1/2.
Hence the theoretical frequencies of getting 0,1,2,3,4,5 heads are the successive terms of the binomial expansion 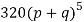
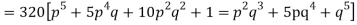 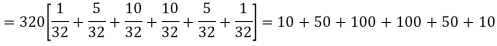 Thus the theoretical frequencies are 10, 50, 100, 100, 50, 10. Hence, 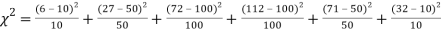 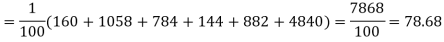 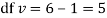
|
Since the calculated value of 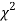 is much greater than
is much greater than 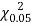 the hypothesis that the data follow the binomial law is rejected.
the hypothesis that the data follow the binomial law is rejected.
Q7) Fit a Poisson distribution to the following data and test for its goodness of fit at level of significance 0.05.
x | 0 | 1 | 2 | 3 | 4 |
f | 419 | 352 | 154 | 56 | 19 |
S8) Mean m =
Hence, the theoretical frequency are 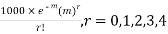
x | 0 | 1 | 2 | 3 | 4 | Total |
f | 404.9 (406.2) | 366 | 165.4 | 49.8 | 11..3 (12.6) | 997.4 |
Hence, 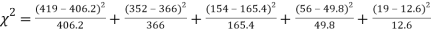 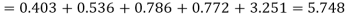 |
Since the mean of the theoretical distribution has been estimated from the given data and the totals have been made to agree, there are two constraints so that the number of degrees of freedom v = 5- 2=3
For v = 3, we have 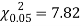
Since the calculated value of 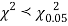 the agreement between the fact and theory is good and hence the Poisson distribution can be fitted to the data.
the agreement between the fact and theory is good and hence the Poisson distribution can be fitted to the data.
Q8) In experiments of pea breeding, the following frequencies of seeds were obtained
Round and yellow | Wrinkled and yellow | Round and green | Wrinkled and green | Total |
316 | 101 | 108 | 32 | 556 |
Theory predicts that the frequencies should be in proportions 9:3:3:1. Examine the correspondence between theory and experiment.
S9) The corresponding frequencies are
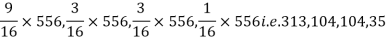 Hence, 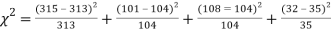  For v = 3, we have 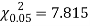
|
Since the calculated value of  is much less than
is much less than 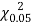 there is a very high degree of agreement between theory and experiment.
there is a very high degree of agreement between theory and experiment.