Unit-3
Fourier, Laplace and Z transform
Q1) Explain the Fourier series Representation of periodic signals?
A1) A signal is said to be periodic if it satisfies the condition x (t) = x (t + T) or x (n) = x (n + N).
Where T = fundamental time period,
ω0= fundamental frequency = 2π/T
There are two basic periodic signals:
x(t) = cos wot (sinusoidal)
x(t) = e jwot (complex exponential)
These two signals are periodic with period T=2π/ω0
A set of harmonically related complex exponentials can be represented as ɸk(t)
ɸk(t) = { e jkwot} = { e jk(2π/T)t} where k=0,±1,±2,±3,………………(1)
All these signals are periodic with period T.
According to orthogonal signal space approximation of a function f(x) with n mutually orthogonal functions is given by
x(t) =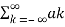 
e jkwot ……………………………………………….(2)
=
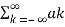k ejkwot
Where ak= Fourier coefficient = coefficient of approximation.
This signal x(t) is also periodic with period T.
Equation 2 represents Fourier series representation of periodic signal x(t).
The term k = 0 is constant.
The term k=±1 having fundamental frequency ω0, is called as 1st harmonics.
The term k=±2 having fundamental frequency 2ω0, is called as 2nd harmonics, and so on...
The term k=±n having fundamental frequency nω0, is called as nth harmonics.
Q2) Write a short note on waveform symmetries?
A2)
- Even function symmetry
A function is defined to be even if and only if
f(t) = f(-t) -------------------------------------------------------------(1)
If the condition is satisfied then eq(1) is said to be even because polynomial functions with even components
For any even periodic functions, the equations for the Fourier coefficients
av = 2/T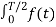 
dt ---------------------------------------------------(2)
ak = 4/T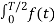 
coskwot dt --------------------------------------------(3)
bk=0 for all k --------------------------------------------------(4)
In eq(4) all b co-effecients are zero if the function is even. The figure depicts the even periodic function.
 |
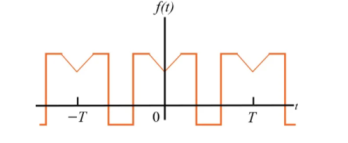Figure 1. Even symmetry
Av = 1/T 
= 1/T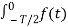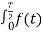  
|
- Odd function symmetry
A periodic function is defined to be odd if
f(t) = -f(t) ---------------------------------(1)
The function that satisfies eq(1) is said to be odd because polynomial funtions with odd exponents. The expression for Fourier co-effecients are:
Av=0
Ak=0 for all k;
Bk = 4T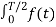
sinkwo dt ---------------------------------(2)
 |
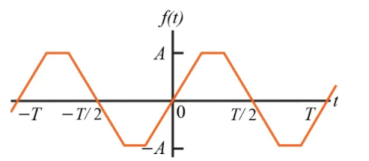Figure 2. Odd function symmetry
- Half Wave Symmetry
A function is said to have half-wave symmetry if it satisfies the following constraint:
f(t) = -f(t - T/2) ------------------------------------ (1)
Equation 1 expresses that a periodic function has a half-wave symmetry if, after it has been shifted by one-half of a period and inverted, it is said to be identical to the original periodic function.
For instance, the periodic functions illustrated in Figures possess half-wave symmetry.
 |
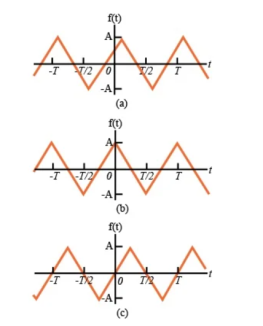Figure 3. Half wave Symmetry
- Quarter Wave Symmetry
If a function has half-wave symmetry and symmetry about the midpoint of the positive and negative half-cycles, the periodic function is said to have quarter--wave symmetry. This function is illustrated in Figure
 |
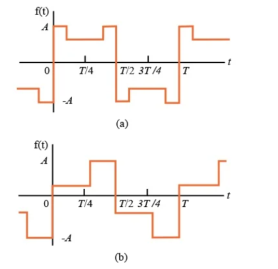Figure 4. Quarter Wave Symmetry
Q3) Explain the calculation of Fourier co-efficient ?
A3) We know that x(t) = 
e jkwot ------------------------(1)
Multiply e-jnwot on both sides we get
x(t) e -jnwot = 
e jkwot . e- jnwot
Consider integral on both sides we get
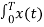e jkwot dt = 
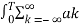e jkwot . e- jnwot
= 
e j(k-n)wot dt
= 
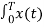e jkwot dt =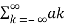 
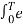j(k-n)wot dt --------------------------(2)
By Eulers formula
j(k-n)wot dt =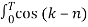 
wo dt + j 
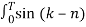wo dt
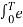j(k-n)wot dt = { T k=n
0 k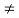 
n
Hence in equation(2) the integral is zero for all values of k except at k=n. Put k=n is equation 2
= 
j(k-n)wot dt = anT
=an = 1/T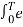 
-jnwot
Replace n by k we get
= ak = 1/T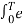 
-jkwot dt
x(t) =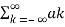
e j(k-n) wot
Where ak = 1/T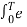 
-jkwot dt
Q4) Derive Fourier Transform?
A4) The (CT) Fourier transform (or spectrum) of x(t) is
X(jw) =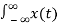 
e -jwt dt ---------------------------------------(1)
x(t) can be reconstructed from its spectrum using the inverse Fourier transform
x(t) = 1/ 2 π 
e jwt dw ------------------------------------------(2)
The above two equations are referred as Fourier transform pair with the first one being the analysis equation and the second being the synthesis equation.
Notation
X(jw) = F{x(t)}
x(t) = F -1 {X(jw)}
x(t) and X(jw) form a Fourier transform pair denoted by
x(t) F X(jw)
Q5) Explain convolution?
A5) Imagine we have a function f[t] whose Fourier transform is F[w] and another function g[t] whose transform is G[w]. Then the convolution is
f[t] * g[t] =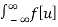 
g[t-u] du
We write g[t-u] in terms of Inverse Fourier transform
g[t-u] = 1/2π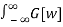 
E Iw(t-u) dw dw
Thus
f[t] * g[t] =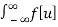 
1/2π 
E Iw(t-u) dw dw du
= 1/2π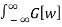 
E Iwt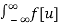 
E -Iwu du dw
But the right hand integral above is the Fourier transform of f[u] so
f[t] * g[t] = 1/2π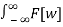 
G[w] E -Iwu dw
The convolution property states that:
x(t) * h(t) > X(w) H(w)
Let
y(t) =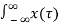 
h(t-τ) dτ = x(t) * h(t)
Y(w) =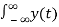 
e -jwt dt = 
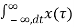h(t-τ) dτ e -jwt dt
If we switch the order of the two integrals we get
Y(w) =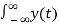 
e -jwt dt =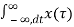 
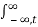h(t-τ) dτ e -jwt dt let u=t-τ
= 
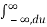h(u) e -jw(u+τ) du dτ
= 
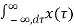e -jwτ dτ 
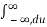h(u) e -jwu du
= X(w) H(w)
Therefore,
y(t) = x(t) * h(t) <-> Y(w) = X(w) H(w)
Fourier Transform of the convolution of two functions is simply the product of the Fourier Transforms of the functions.
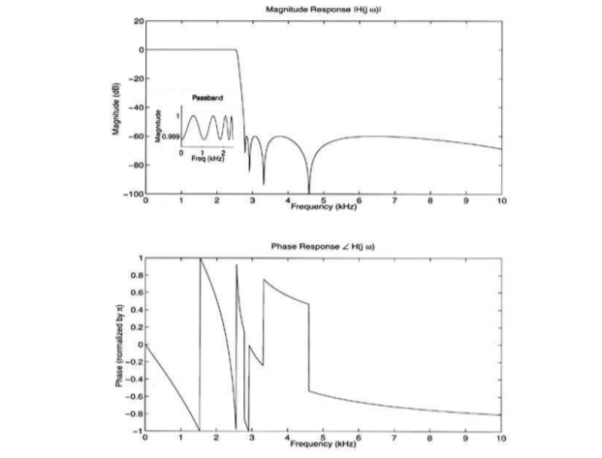
Q6) Explain the magnitude and phase response?
A6) H(e jw) = H R ( e jw) + j H I ( e jw) = | H ( e jw) | e j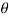 
1 (w)
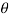1 (w) = angle H(e jw)
Example:
h[n] = - δ[n]
| H (ejw)| = 1 angle H(e jw) = π
In the magnitude or phase representation a real valued frequency response does not mean that the system is zero-phase.
Using this representation,
|Y (e jw) | = | H ( ejw)| | X (ejw)|
 |
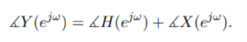Thus, |H(ejω)| and angle H(ejω) are commonly referred to as the gain and the phase shift of the system, respectively.
In magnitude and phase plots, as ω goes through a zero on the unit circle, the magnitude will go to zero and the phase will flip by π, as shown in the figure below.
|
Figure . Magnitude and Phase response
Q7) Explain DTFT?
A7) The discrete-time Fourier transform (DTFT) or the Fourier transform of a discrete–time sequence x[n] is a representation of the sequence in terms of the complex exponential sequence ejωn.
The DTFT sequence x[n] is given by
X(w) = 
e-jwn ---------------(1)
Here X(w) is a complex function of real frequency variable w and can be written as
X(w) = Xre (w) + j X img(w)
Where Xre (w) , j X img(w) are real and Imaginary parts of X(w)
Xre(w) = |X(w)| cos 
(w)
Ximg(w) = |X(w)| sin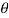 
(w)
|X(w)| 2 = |Xre(w)| 2 + |Xim(w)| 2
And | X(w)| can be represented as
X(w) = |X(w)| e j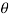
(w)
Inverse Discrete Fourier Transform is given by
x(n) = 1/2π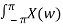 
e jwn dw
Q8) Find the DFT of the sequence f(n) ={ 8,4,8,0}
A8) F[n] =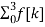 
e -j π/2 nk = 
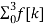(-j) nk
 |
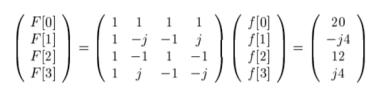
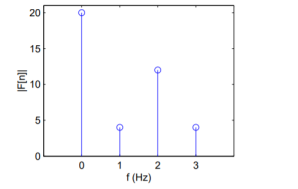Figure. Magnitude of the four point sequence.
Q9) Explain Parseval’s theorem?
A9) Consider two periodic signals x1(t) and x2(t) with equal period T. If the Fourier series co-efficient of these two signals are cn and dn then
1/T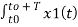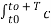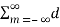   
= 1/T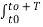  
= 0 n≠ m
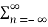=  If x1(t) = x2(t) = x(t) then eq(3) becomes 1/T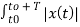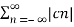  
The above equation can be written as
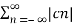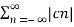  n≠0
= c0 2 + 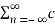 n≠0 a0 2 +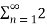 
= a0 2 +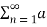 
|
Q10) Find H(z), poles and zeros for the difference equation given by
A10) y[n] – 3/8 y[n-1] – 7/16 y[n-2] = x[n] + x[n-2]
Solution:
Here ao=1,a1=-3/8,a2=-7/6,bo=1,b1=0,b2=1
H[z] = 1 + z -2 / 1 -3/8 z-1 -7/16 z -2
= (1+j z-1 ) (1 -jz-1) / (1-7/8 z-1) ( 1+1/2 z-1)
Zeros : z=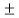
j represented by o.
Poles z= 7/8 , z=-1/2 represented by x.
Poles and Zeros
|
